人教版七年级下册6.1 平方根教学课件ppt

这是一份人教版七年级下册6.1 平方根教学课件ppt，文件包含《61平方根3》精品课件pptx、《61平方根3》同步练习docx、《61平方根3》精品教学方案doc等3份课件配套教学资源，其中PPT共25页， 欢迎下载使用。

平方根的概念及性质。平方根和算术平方根的联系与区别.
了解平方根、 开平方的概念;明确算术平方根与平方根的区别和联系.能用符号正确地表示一个数的平方根，理解开方运算和乘方运算之间的互逆关系;
如果一个正数x的平方等于a，即x²a,那么这个正数x叫做a的算术平方根，a的算术平方根记为 ，读作“根号a”，a叫做被开方数.
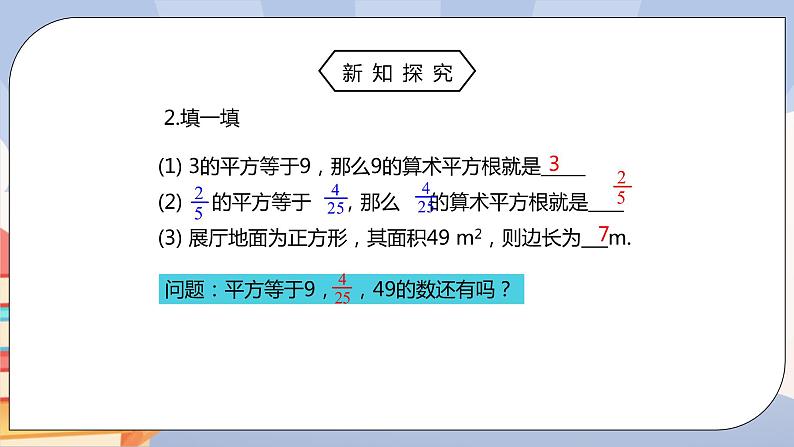
(1) 3的平方等于9，那么9的算术平方根就是_____(2) 的平方等于 ，那么 的算术平方根就是____(3) 展厅地面为正方形，其面积49 m2，则边长为___m.
想一想 3和-3有什么特征？
如果一个数的平方等于9，这个数是多少？
问题2 根据上面的研究过程填表：
想一想：如果我们把 　 分别叫做 　 的平方根，你能给出平方根的概念吗？
一般地，如果一个数x的平方等于a，即x2=a，那么这个数x就叫做a的平方根，也叫做a的二次方根.
例如：9的平方根为3和－3，
平方根的表示方法、读法
（2）2是4的平方根； （ ）
（3）-5是25的平方根；（ ）
（4）64的平方根是±8；（ ）
（5）-16的平方根是-4．（ ）
判断下列说法是否正确.
（1）49的平方根是7；（ ）
求一个数a的平方根的运算，叫做开平方.
平方运算与开平方运算互为逆运算.
平方与开平方有什么关系？
（1）0； （2） （3）0.000196； （4）-81.
1.正数有两个平方根，它们互为相反数.2. 0 的平方根还是0.3. 负数没有平方根.
正数的平方根有什么特点？0 的平方根是多少？负数有平方根吗？
符号 只有符合a≥0时有意义， a＜0时无意义，你知道为什么吗？
根据平方根的概念或性质.
你能总结一下平方根与算术平方根的区别与联系吗？
联系：（1）包含关系：平方根包含算术平方根，算术平方根是平方根的一种.（2）只有非负数才有平方根和算术平方根.（3）0的平方根是0，算术平方根也是0.
区别：（1）个数不同：一个正数有两个平方根，但只有一个算术平方根. （2）表示法不同：平方根表示为 ， 而算术平方根表示为 .
解：(1) 因为 (±10)2 = 100，所以 100 的平方根是 ±10；
(3)因为 (±0.5)2 = 0.25，所以 0.25 的平方根是 ±0.5.
1.下列个数有平方根吗？如果有，写出它的平方根，如果没有，说明理由.
（1）有平方根，±8；
（5）没有平方根，负数没有平方根.
解：(1)(11)2 =121，它的算术平方根是 11，平方根是 11.
3.如果一个数的两个平方根时a+3,2a-15,那么这个数是多少？
因为一个数正数的两个平方根互为相反数，所以（a+3）+（2a-15）=0,解得a=4，当a=4，a+3=7，2a-15=-7.即这个数是7，-7.
1、一个数的算术平方根是5，则这个数的平方根为( )A．25 B．±25C．－5 D．±52、一个数的平方根就是这个数的算术平方根，这个数是( )A．1 B．0C．－1 D．1或0
3．已知a－1和5－2a都是m的平方根，求a与m的值.解：根据题意，分以下两种情况：①当a＝1与5－2a是同一个平方根时，则a－1＝5－2a，解得a＝2.此时，m＝(2－1)2＝1；②当a－1与5－2a是两个平方根时，则a－1＋5－2a＝0，解得a＝4.此时，m＝(4－1)2＝9.综上所述，当a＝2时，m＝1；当a＝4时，m＝9
4.求下列各式中 x 的值：
（1）x2 = 25；（2）x2 – 81 = 0；（3）25x2 = 36.
正数有两个平方根，两个平方根互为相反数