高中数学北师大版 (2019)必修 第一册3.2 基本不等式课后练习题

这是一份高中数学北师大版 (2019)必修 第一册3.2 基本不等式课后练习题，共18页。试卷主要包含了实数‍a，b‍大小的比较，性质‍1‍，性质‍2‍，性质‍3，性质‍4‍，性质‍5，性质‍6，基本不等式等内容，欢迎下载使用。
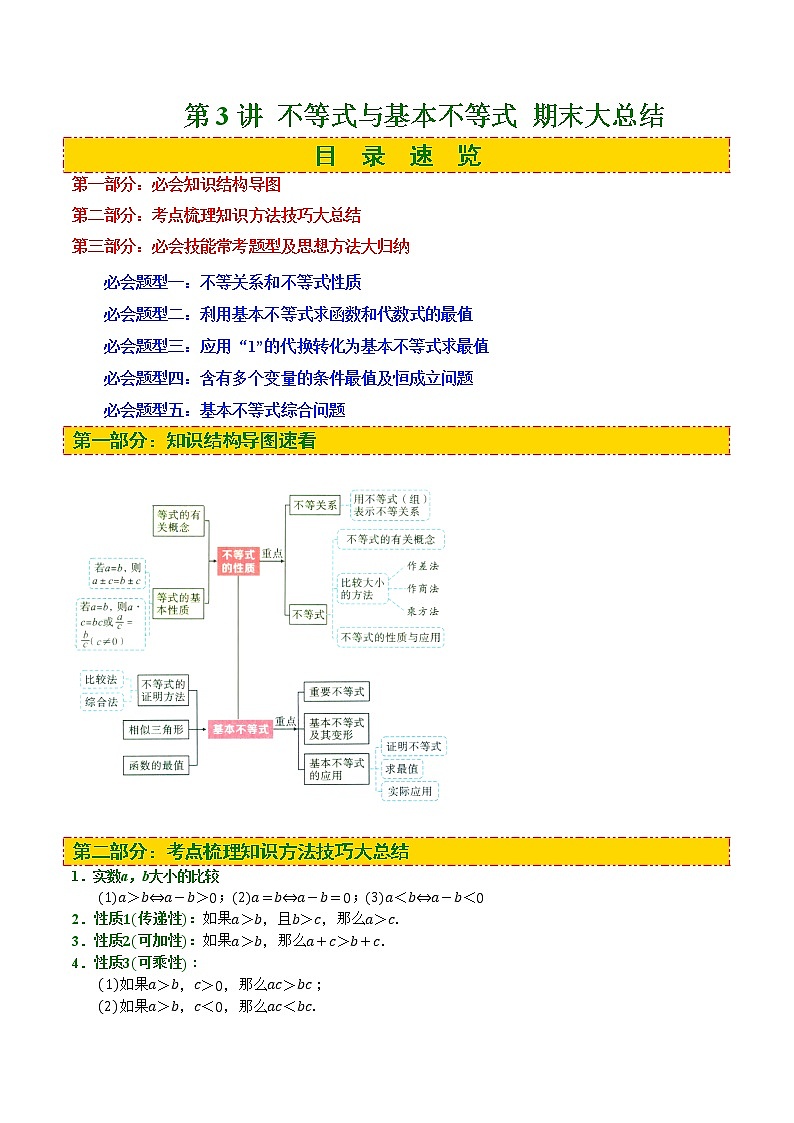
第3讲 不等式与基本不等式 期末大总结目  录  速  览第一部分：必会知识结构导图第二部分：考点梳理知识方法技巧大总结第三部分：必会技能常考题型及思想方法大归纳必会题型一：不等关系和不等式性质必会题型二：利用基本不等式求函数和代数式的最值必会题型三：应用“1”的代换转化为基本不等式求最值必会题型四：含有多个变量的条件最值及恒成立问题必会题型五：基本不等式综合问题第一部分：知识结构导图速看第二部分：考点梳理知识方法技巧大总结1．实数‍a，b‍大小的比较；；2．性质‍‍传递性‍‍：如果‍‍且‍那么‍‍3．性质‍‍可加性‍‍：‍如果‍那么‍‍4．性质‍‍可乘性‍‍如果‍‍那么‍‍如果‍‍那么5．性质‍4(‍同向可加性‍)‍：如果‍那么‍．6．性质‍5(‍同向同正可乘性‍)：‍如果‍‍那么‍‍如果‍‍那么‍推论‍‍正数乘方性‍‍当‍‍时其中‍‍7．性质‍6(‍正数开方性‍)：‍当‍‍时‍其中‍8．基本不等式对于任意实数‍‍和‍‍总是成立的，即‍‍所以‍‍当且仅当‍‍时，等号成立．设‍‍取‍‍代入上述不等式可得‍当且仅当‍‍时，等号成立．这个不等式称为基本不等式，其中，‍‍称为‍‍的算术平均值‍称为‍‍的几何平均值．‍因此，基本不等式又称为均值不等式．9．一个不等式链：0‍)，当且仅当‍‍时等号成立，‍其中‍‍分别叫作正数的调和平均数，几何平均数、算术平‍均数、平方平均数．10．当‍‍均为正数时，下面的命题均成立：(1)‍若‍‍为定值‍则当且仅当‍‍时，‍‍取得最大值‍(2)‍若‍‍为定值‍‍则当且仅当‍‍时，‍‍取得最小值‍．第三部分：必会技能常考题型及思想方法大归纳必会题型一：不等关系和不等式性质1．(2022·青海·海南藏族自治州高级中学高一阶段练习)下列命题中正确的是(    )A．若，则 B．若，则C．若，则 D．若，则【答案】A【分析】利用不等式性质，作差法及特殊值法即可判断四个选项．【解析】对于A，，∵，∴，，∴，即，故A正确；对于B，当时，，故B错误；对于C，当时，满足，但是不成立，故C错误，对于D，取，，，，则，故D错误．故选：A．2．[多选](2022·黑龙江·大庆实验中学高一阶段练习)下列结论中不正确的是(    )A．若，则 B．若，则C．若，，则 D．若，则【答案】BC【分析】利用不等式的性质判断选项A；求得不等式的解判断选项B；举反例否定选项C；求得不等式的解判断选项D．【解析】选项A：若，则，则．判断正确；选项B：若，则或或．判断错误；选项C：令，，则．判断错误；选项D：若，则，则．判断正确．故选：BC3．[多选](2022·山东青岛·高一期中)对实数a，b，c，下列说法正确的是(    )A．若，则 B．若，则C．若则 D．恒成立【答案】AD【分析】由不等式的性质可判断A；取特值可判断B，C；作差判断D．【解析】对于A，若，则，故A正确；对于B，若，，则，则，故B不正确；对于C，若，满足，，则C不正确；对于D，，所以，故D正确．故选：AD．4．(2022·辽宁·建平县实验中学高一阶段练习)(1)若，求的取值范围；(2)已知，，求的取值范围．【答案】(1)；(2)【分析】(1)根据不等式的性质计算可得．(2)设，整理后利用系数相等求得与的值，再由已知结合不等式的性质求解．【解析】(1)因为，即，，所以， 所以，又，所以，即．(2)设， ，解得，．，， ，，则．的取值范围是． 必会题型二：利用基本不等式求函数和代数式的最值1．(2022·北京市昌平区前锋学校高一期中)已知，则的最小值是(    )A．2 B．3 C．4 D．5【答案】D【分析】利用均值不等式求解即可．【解析】由题意，，故，根据均值不等式，，当且仅当，即时等号成立．故的最小值是5．故选：D2．(2022·江苏·常州田家炳高中高一期中)已知，那么的最小值为(    )A． B． C． D．【答案】B【分析】利用基本不等式可求得，可所求式子，再次利用基本不等式可求得结果．【解析】，，，(当且仅当且，即，时取等号)，的最小值为．故选：B．3．(2022·海南·海口中学高一期中)当时，则的最大值为______．【答案】【分析】对代数式形式进行化简，得到基本不等式形式，根据基本不等式，得到答案．【解析】由题意，，故当且仅当，即时，等号成立．故答案为：4．(2022·浙江·高一期中)若，则的最小值是__________【答案】【分析】将变形，得到，利用基本不等式“1”的妙用，求解最小值．【解析】因为，所以，，所以，当且仅当，即时等号成立．故答案为：．5．(2022·江苏·常州田家炳高中高一期中)已知正实数满足：．(1)求的最小值；(2)求的最小值．【答案】(1)25(2)11【分析】(1)利用均值不等式可得，令，转化为二次不等式求解即可；(2)转化原式为，则，结合均值不等式，即得解．【解析】(1)正实数令，则，原不等式可化简为：解得(舍)或，即当且仅当即取得“”的最小值为25(2)由得，即由正实数，得当且仅当取得“”的最小值为11． 必会题型三：应用“1”的代换转化为基本不等式求最值1．(2023·四川资阳·模拟预测)已知a，b均为正数，且，则的最小值为(    )A．8 B．16 C．24 D．32【答案】B【分析】根据“1”的变形技巧及均值不等式求解即可．【解析】因为a，b均为正数，且，所以，当且仅当时，即时等号成立，故选：B2．(2022·安徽·砀山中学高三阶段练习)若正实数x，y满足，则(    )A．有最小值8 B．有最小值9 C．有最大值8 D．有最大值9【答案】B【分析】根据条件将化为，所以可看成，化简后利用基本不等式求出式子的最小值即可．【解析】由得，则，当且仅当时等号成立，故有最小值9．故选：B．3．(2022·四川成都·高二期中)已知，，且，则当取最小值时，=______．【答案】【分析】变换得到，展开利用均值不等式计算得到答案．【解析】，当，即，时等号成立，此时．故答案为：4．(2022·上海市松江二中高一期中)已知，则的最小值为__________．【答案】【分析】先判断得每一项均为正，然后利用两个分布的关系得，利用均值不等式计算即可．【解析】因为，所以， ，显然，，所以，当，即时，等号成立，所以 ，所以的最小值为．故答案为：5．(2022·上海交通大学附属中学浦东实验高中高一期中)已知，，．(1)求的最小值；(2)求的最大值；【答案】(1)(2)【分析】(1)首先根据，可得，然后使用基本不等式 “1”的妙用进行求解最值即可．(2)首先先将原式平方，然后利用基本不等式求解最大值即可．【解析】(1)，，，，，当且仅当，即时等号成立．的最小值为．(2)，当且仅当，即，时等号成立，，故的最大值为． 必会题型四：含有多个变量的条件最值及恒成立问题1．(2022·江苏省奔牛高级中学高一阶段练习)实数a，b，c满足，，，则的最小值为(    )A． B．1 C． D．【答案】B【分析】利用因式分式法，结合分式的运算性质、基本不等式进行求解即可．【解析】，，，，，当且仅当，即时等号成立，的最小值为1，故选：B2．(2022·江苏·星海实验中学高一期中)若正实数，，满足，则的最大值为(    )A．2 B．3 C．4 D．6【答案】C【分析】利用等式变形构造基本不等式即可得所求得最大值【解析】由正实数，，满足所以即所以当时取到等号，所以最大值为：4故选：C．3．[多选](2022·江苏省扬中高级中学高一期中)已知正实数满足，当取最小值时，下列说法正确的是(    )A． B．C．的最大值为1 D．的最小值为【答案】AC【分析】由，代入用基本不等式求得最小值，得结论判断A，此处条件代入已知得可判断B，判断AB过程中两个结论代入后利用二次函数性质求得最值判断CD．【解析】∵正实数满足，∴，当且仅当，即时等号成立，A正确；时，，B错；，，即时，的最大值1，C正确D错误．故选：AC．4．(2022·江苏南通·高一期中)若不等式，对一切恒成立，则实数的取值范围(    )A． B． C． D．【答案】A【分析】采用分离常数法，易得，结合拼凑法和基本不等式可得，进而得解．【解析】不等式对一切恒成立，，，对一切恒成立．而 ，当且仅当，即时等号成立，．故选：5．(2022·上海·华师大二附中高一期中)已知正实数x、y满足．(1)求xy的最小值，并求取最小值时x、y的值；(2)若的最小值为9，求a的值．【答案】(1)8，，(2)2【分析】(1)利用基本不等式求最小值即可；(2)利用基本不等式得到，然后列方程，解方程即可．【解析】(1)，即，解得，当且仅当，即，时等号成立，所以的最小值为8，此时，，．(2)由得，则，所以，令，则，解得或－4(舍去)，所以，当时，，解得，所以时，取得最小值9，满足要求，所以． 必会题型五：基本不等式综合问题1．(2022·辽宁·高三期中)若正实数x，y满足x＋2y＋xy＝7，则x＋y的最小值为(    )A．6 B．5 C．4 D．3【答案】D【分析】由，得，，利用基本不等式求解即可．【解析】因为x＋2y＋xy＝7，所以，所以．因为，则所以，当且仅当，即x＝1，y＝2时，等号成立，所以x＋y的最小值为3．故选：D2．[多选](2022·陕西·西安南开高级中学高一期中)下列命题中，正确的是(    )①若，则；②若，则；③若，则；④若，则A．① B．② C．③ D．④【答案】ABC【分析】结合基本不等式、差比较法、不等式的性质等知识确定正确答案．【解析】①，，当且仅当时等号成立，①正确．②，，，当且仅当时，等号成立，②正确．③，，当时等号成立，所以，③正确．④，，如，则，所以④错误．故选：ABC3．(2022·上海·高一专题练习)若，，且，则下列不等式中恒成立的是(　　)A． B． C． D．【答案】B【分析】根据不等式的性质及基本不等式可判断A、C项，对于D举出反例即可，通过“1”的代换，可证明B项．【解析】因为，，所以， 又，所以，，所以，，A错误；根据基本不等式，，当x = y =2时等号成立，C错误；令，则，D错误；对于B项，，则，则，当x = y =2时等号成立，B项正确．故选：B．4．[多选](2022·山东济南·高一期中)若正实数a，b满足，则下列说法正确的是(    )A．最大值为 B．最小值为C．ab最小值为 D．最小值为【答案】ABD【分析】对A，B，C选项，结合基本不等式进行求最值即可；D选项将等式构造变形为与相乘化成能用基本不等式的形式即可．【解析】对A选项：由 ，，则，当且仅当时等号成立，故A正确；对B选项；，当且仅当时等号成立，故B正确；对C选项；因为，，所以当且仅当时等号成立，故C不正确；对D选项；因为，，所以 当且仅当时等号成立，故D正确；故选：ABD．5．[多选](2021·江西省遂川中学高一阶段练习)下列结论中，所有正确的结论是(    )A．若，则函数的最大值为B．若，，则的最小值为C．若，，，则的最大值为4D．若，，，则的最小值为【答案】BC【分析】A选项，由，则，将构造出不等式的形式B选项，，并且，所以，并且，等式化“1”，然后利用基本不等式，C选项，由，，，以及，构造出关于的二次不等式解之分析，D选项，由，，，配凑，然后等式化“1”，构造基本不等式．【解析】选项A：由，则，又， 当且仅当时等号成立，故A错误；选项B：，并且，所以，并且，则，当且仅当时，即时等号成立，故B正确；选项C：由x，，，即，即解得当且仅当时，有最大值4，故C正确选项D：若，，，则，所以 ，当且仅当时取等号，故D错误；故选：BC．6．(2022·浙江杭州·高一期中)已知a，b为正实数且，求下列式子的最值(1)求的最大值;(2)求的最小值;(3)求的最小值．【答案】(1)(2)(3)9【分析】(1)利用不等式计算即可；(2)根据基本不等式“1”的用法，将小问中分母与构造为相乘可约的形式；(3)根据化简式子，再根据不等式求出最小值．【解析】(1)当且仅当取到最大值(2)当且仅当，时取到最小值(3)当且仅当时取到最小值97．(2022·广东·深圳外国语学校致远高中高一阶段练习)为加强“疫情防控”，某校决定在学校门口借助一侧原有墙体，建造一间墙高为4米，底面积为32平方米，且背面靠墙的长方体形状的校园应急室，由于此应急室后背靠墙，无需建造费用，某公司给出的报价为：应急室正面和侧面报价均为每平方米200元，屋顶和地面报价共计7200元，设应急室的左右两侧的长度均为米，公司整体报价为元．(1)试求关于的函数解析式；(2)公司应如何设计应急室正面和两侧的长度，可以使学校的建造费用最低，并求出此最低费用．【答案】(1)(2)正面长度为8米,两侧长度为4米,建造费用最低,最低20000元．【分析】(1)首先得到正面长度为米，根据题意写出总价即可．(2)，利用基本不定式即可求出最值．【解析】(1)因应急室的左右两侧的长度均为米,则应急室正面的长度为米,于是得(2)，当且仅当，即时等号成立，此时在内，，故正面长度为8米，两侧长度为4米，建造费用最低，最低20000元．8．(2022·山东德州·高三期中)第二届中国(宁夏)国际葡萄酒文化旅游博览会于2022年9月6—12日在银川市成功举办，某酒庄带来了葡萄酒新品参展，与采购商洽谈，并计划大量销往海内外．已知该新品年固定生产成本40万元，每生产一箱需另投入100元．若该酒庄一年内生产该葡萄酒万箱且全部售完，每万箱的销售收入为万元，(1)写出年利润(万元)关于年产是(万箱)的函数解析式(利润销售收入成本)；(2)年产量为多少万箱时，该酒庄的利润最大？并求出最大利润．【答案】(1)(2)年产量为29万箱时，该公司利润最大，最大利润为2370万元【分析】(1)分和两种情况讨论，根据利润销售收入成本得到函数解析式；(2)根据二次函数及基本不等式求出函数的最大值，即可得解．【解析】(1)解：当时，，当时，，故；(2)解：当时，，对称轴为，开口向下，故，当时，，当且仅当，即时，等号成立，因为 ，所以当时，利润最大，最大值为万元，故年产量为万箱时，该公司利润最大，最大利润为万元．