

2023届甘肃省张掖市某重点校高三上学期12月月考数学(理)试题含解析
展开2023届甘肃省张掖市某重点校高三上学期12月月考数学(理)试题
一、单选题
1.若集合,,则( )
A. B. C. D.
【答案】B
【分析】解出集合中对应的不等式,然后可得答案.
【详解】∵集合,,
∴,
故选:B.
2.已知,是复数的共轭复数,则复数( )
A. B. C. D.
【答案】D
【分析】根据共轭复数的概念和复数的四则运算即可求解.
【详解】因为,是复数的共轭复数,所以,
则复数,∴复数,
故选:D.
3.已知命题:,或,则( )
A.:,或 B.:,且
C.:,且 D.:,或
【答案】B
【分析】由含有一个量词的命题的否定的定义求解.
【详解】解:由题意知,命题:,或是全称量词命题,
所以其否定为存在量词命题,即:,且,
故选:B.
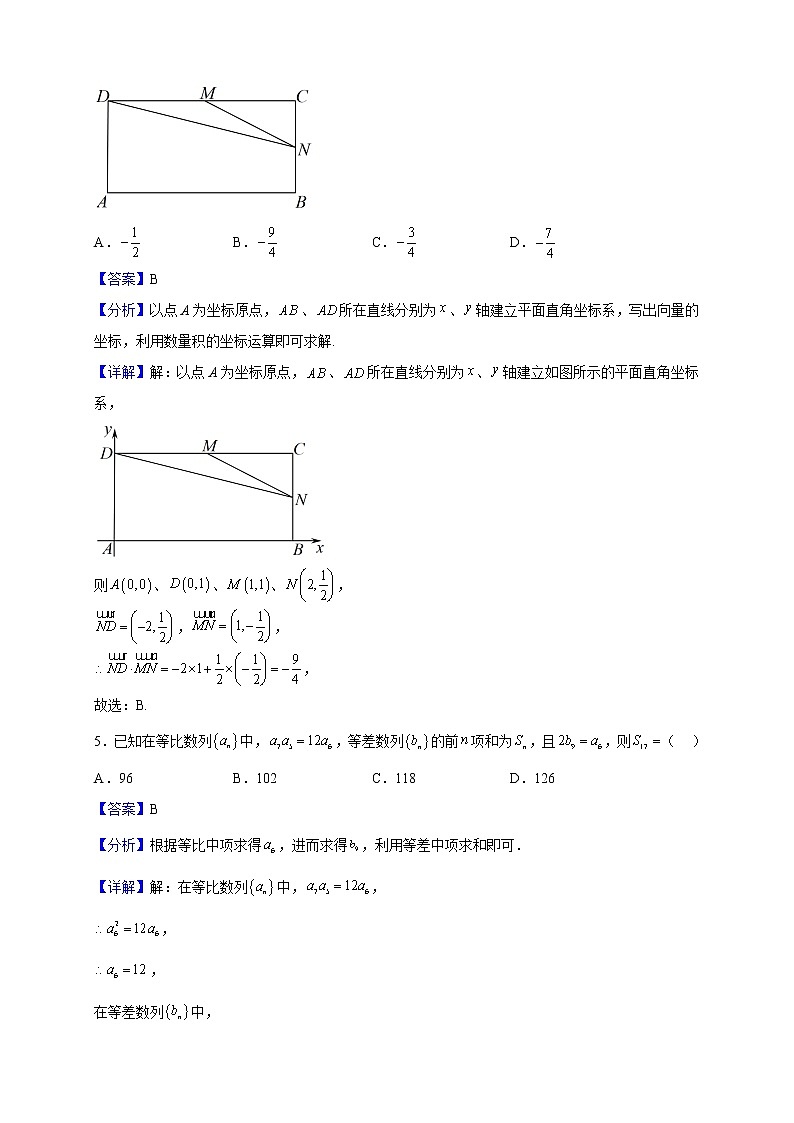
4.在矩形中,,,若点、分别是,的中点,则( )
A. B. C. D.
【答案】B
【分析】以点A为坐标原点,、所在直线分别为、轴建立平面直角坐标系,写出向量的坐标,利用数量积的坐标运算即可求解.
【详解】解:以点A为坐标原点,、所在直线分别为、轴建立如图所示的平面直角坐标系,
则、、、,
,,
,
故选:B.
5.已知在等比数列中,,等差数列的前项和为,且,则( )
A.96 B.102 C.118 D.126
【答案】B
【分析】根据等比中项求得,进而求得,利用等差中项求和即可.
【详解】解:在等比数列中,,
,
,
在等差数列中,
,
,
,
故选:B.
6.按照如图所示的程序框图,其运行的结果为( )
A. B.
C. D.
【答案】D
【分析】根据程序框图判断出变量i每次自增2,其终止程序运行的i值为101,但是加和只算到99,进而可以求出答案.
【详解】根据程序框图可知,其终止程序运行的i值为101,
程序框图计算结果为:,
故选:D.
7.在崂山的山脚下临海断崖南侧,距岸百米处有一座石柱,形如老人坐在碧波之中,人称“石老人”.老人以手托腮,注目凝神,每天晨迎旭日,暮送晚霞,伴着潮起潮落,历尽沧桑,不知度过了多少岁月.这个由大自然鬼斧神工雕凿的艺术杰作,已成为石老人国家旅游度假区的重要标志,若该景区在开放时间内,每半个小时会有一趟观光车从景区入口发车,有一名学生周日上午某时刻到达景区入口,准备乘坐观光车,则他等待时间不多于10分钟的概率为( )
A. B. C. D.
【答案】D
【分析】由题意,等待时间的区间为,而等待时间不多于10分钟的等待时间区间为,根据几何概型求解即可.
【详解】解:由题意,观光车的发车间隔为30分钟,即等待时间的区间为,设等待时间为,则等待时间不多于10分钟的等待时间区间为,由几何概型可得,等待时间不多于10分钟的概率为.
故选:D.
8.《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑.在鳖臑中,平面,则鳖臑外接球的表面积是( )
A. B. C. D.
【答案】A
【分析】判段出补全后为长方体,再利用长方体外接圆半径的计算公式得出半径,即可直接得出答案.
【详解】由题意可知,
如图,将鳖臑补全成长方体,
则鳖臑外接球的半径,
故鳖臑外接球的表面积为.
故选:A.
9.安徽省地形具有平原、台地(岗地)、丘陵、山地等类型,其中丘陵地区占了很大比重,因此山地较多,著名的山也有很多,比如:黄山、九华山、天柱山.某校开设了研学旅行课程,计划将5名优秀学生分别派往这三个地方进行研学旅行,每座山至少有一名学生参加,则不同的安排方案种数是( )
A.150 B.120 C.160 D.180
【答案】A
【分析】先分成三组,可以3、1、1,也可以2、2、1,分好后再安排到三个山.
【详解】根据题意,分2步进行分析:①将5名优秀学生分为3组,若分为3、1、1的三组,有种分组方法,若分为2、2、1的三组,有种分组方法,故共有种分组方法,②将分好的3组安排到3个地方进行研学旅行,有种情况,则有种安排方法.
故选:A.
10.已知抛物线的焦点,过的直线与交于,两点,准线与轴的交点为,当时,直线的方程为( )
A. B. C. D.
【答案】B
【分析】由交点坐标可得抛物线方程,设直线的方程为,,,将直线方程和抛物线方程联立,利用韦达定理和数量积的坐标表示求的值即可.
【详解】由已知可得,所以,,故抛物线,
又因为且直线斜率不为0,设直线的方程为,,,
由,得,,,
,所以,,
由,得,
所以即,
所以,解得,
所以直线的方程为:.
故选:B
11.在正方体中,,分别为,的中点,则( )
A.平面 B.异面直线与所成的角为30°
C.平面平面 D.平面平面
【答案】D
【分析】A项反证法可得;
B项由平移法计算异面直线所成角;
C项由面面平行的判断和性质可得结果;
D项建立空间直角坐标系可得结果.
【详解】对于选项A,假设面 ,则,这与已知与不垂直相矛盾,所以假设不成立.
故选项A错误;
对于选项B,连接,,
因为,所以为异面直线与所成的角或补角,
又因为△为等边三角形,所以,故选项B错误;
对于选项C,
因为,,由面面平行的判定定理可得平面平面,而平面与平面相交,所以平面与平面也相交,故选项C错误;
对于选项D,以为坐标原点,,,所在的直线分别为,,轴,建立空间直角坐标系,如图所示,
设正方体的棱长为1,则,,,,可得,,,设平面的法向量为,
则 ,可取,则,,即,
设平面的法向量为,则,
可取,则,,可得平面的一个法向量为,
由,所以,即平面平面,故选项D正确.
故选:D.
12.已知为坐标原点,双曲线的渐近线方程是,且经过点,过的右焦点的直线与两条渐近线分别交于点,,以为直径的圆过点,则下列说法不正确的是( )
A.双曲线的标准方程为 B.直线的倾斜角为或
C.圆的面积等于 D.与的面积之比为
【答案】D
【分析】设双曲线方程为,代入求出双曲线的标准方程可判断A;
,根据渐近线方程和倾斜角可得直线的倾斜角可判断B;根据双曲线的对称性,设的倾斜角为,求出直线的方程分别与两条渐近线方程联立,解得,点坐标,求出得圆的半径,求出圆的面积可判断C; 为与的公共边, 与的面积之比等于可判断D.
【详解】对于A,∵双曲线的渐近线为,∴设双曲线方程为,∵双曲线经过点,∴,得.∴双曲线的标准方程为,故A正确;
对于B,∵以为直径的圆过点,∴,又渐近线方程为,可得渐近线的倾斜角分别为,,则,,则直线的倾斜角为或,故B正确;
对于C,根据双曲线的对称性,不妨设的倾斜角为,由,可得直线的方程为,分别与两条渐近线方程联立,解得,,此时,故圆的半径,其面积为,故C正确;对于D,∵为与的公共边,∴与的面积之比等于,故与的面积之比为,故D错误.
故选:D.
二、填空题
13.函数在处有极值,则的最小值为______.
【答案】##
【分析】由在处有极值,可得,后由基本不等式可得答案.
【详解】由题意得,因为在处有极值,
则,故.
则,
当且仅当即,时取等号.经检验函数在x=1取得极值成立
故答案为:.
14.已知锐角满足,则______.
【答案】##
【分析】二倍角公示化简,可以得到的正切值,然后将要求解的关系式结合同角平方关系写成分式,将正余弦化切,代入即可得到结果.
【详解】∵,∴,
即,又∵为锐角,∴,∴,即,∴,
故有:.
故答案为:.
15.已知定义在R上的函数,满足,且当时,,则满足不等式的的取值范围是______.
【答案】
【分析】求出当时的解析式,并判断出的单调区间, 讨论的正负确定的符号,从而解得原不等式的解集.
【详解】
因为,即,所以为奇函数,
因为当时,,当时,,,
故在时单调递减,在时单调递减,
又,,,
由得或或或,
解得,
故答案为:.
16.函数的部分图像如图所示,则下列结论正确的是______.
①若把函数的图像向右平移个单位长度,得到函数的图像,则函数是奇函数;
②函数的图像关于点对称;
③函数在单调递减;
④该图像先向右平移个单位,再把图像上所有的点横坐标伸长为原来的2倍(纵坐标不变),可得的图像;
⑤,若恒成立,则实数的取值范围为.
【答案】①②④⑤
【分析】根据函数图像,先求出 的解析式,再逐项分析.
【详解】由图像可知:的最小正周期,∴;
∴,解得:,又,∴,
∴;
对于①,的图像向右平移个单位长度得:,∴,即为奇函数,故①正确;
对于②,令,求得,可得函数的图像关于点对称,故②正确;
对于③,在上,,函数不单调,故③错误;
对于④,把的图像先向右平移个单位,可得的图像;
再把图像上所有的点横坐标伸长为原来的2倍(纵坐标不变),可得的图像,故④正确;
对于⑤,,由得:,
当时,,∴,
∴,
∴,即实数的取值范围为,故⑤正确;
故答案为:①②④⑤.
三、解答题
17.已知的内角,,所对的边分别为,,,.
(1)求角;
(2)若为的中点,且的面积为,,求的长.
【答案】(1)
(2)
【分析】(1)由正弦定理及两角和的正弦公式化简即可得出答案;
(2)由面积公式及余弦定理求解即可.
【详解】(1)由,根据正弦定理可得,得,得
,∵,,
∴,∴,即.
(2)根据题意可知,的面积为,
故,解得;
在中,利用余弦定理可得:,
化简求解得:,故,
在和中,,
,因为,
不难求得:.
18.文旅部门统计了某网红景点在2022年3月至7月的旅游收入(单位:万),得到以下数据:
月份 | 3 | 4 | 5 | 6 | 7 |
旅游收入 | 10 | 12 | 11 | 12 | 20 |
(1)根据表中所给数据,用相关系数加以判断,是否可用线性回归模型拟合与的关系?若可以,求出关于之间的线性回归方程;若不可以,请说明理由;
(2)为调查游客对该景点的评价情况,随机抽查了200名游客,得到如下列联表,请填写下面的列联表,依据的独立性检验,能否认为“游客是否喜欢该网红景点与性别有关联”.
| 喜欢 | 不喜欢 | 总计 |
男 |
|
| 100 |
女 |
| 60 |
|
总计 | 110 |
|
|
参考公式:相关系数,参考数据:.线性回归方程:,其中,.
临界值表:
【答案】(1)可用线性回归模型拟合与的关系,;
(2)列联表见解析,游客是否喜欢该网红景点与性别有关联.
【分析】(1)根据相关系数公式求出相关系数,再应用最小二乘法求回归直线即可;
(2)由已知写出列联表,根据卡方公式求卡方值,结合独立检验的基本思想得到结论.
【详解】(1)由已知得:,
,因为,
说明与的线性相关关系很强.,可用线性回归模型拟合与的关系,
,
则关于的线性回归方程为:.
(2)列联表如下所示:
| 喜欢 | 不喜欢 | 总计 |
男 | 70 | 30 | 100 |
女 | 40 | 60 | 100 |
总计 | 110 | 90 | 200 |
零假设:游客是否喜欢该网红景点与性别无关联,
根据列联表中数据,,
依据小概率值的独立性检验,我们推断不成立,
即游客是否喜欢该网红景点与性别有关联.
19.已知椭圆:的离心率为,直线交椭圆的弦长为.
(1)求椭圆的方程;
(2)经过定点的直线交椭圆于两点,椭圆的右顶点为,设直线,的斜率分别为,,求证:恒为定值.
【答案】(1)
(2)证明见解析
【分析】根据韦达定理得弦长公式,结合离心率即可求解,进而得椭圆方程.
联立直线与椭圆的方程,得到根与系数的关系,根据两点的斜率公式,即可化简求解.
【详解】(1)∵,则,,∴即为:
把代入整理得:,则,
这时,,∴
∴所求的方程为:
(2)由题意可知,直线斜率存在.
设:即代入椭圆方程整理得:
∴,又
,同理
∴
【方法二】平移坐标轴以为原点,这时的方程为
设:代入椭圆方程整理得:
,则,
这时,
20.如图,在直三棱柱中,,,.
(1)证明:平面平面;
(2)求二面角的大小.
【答案】(1)证明见解析
(2).
【分析】(1)通过证明平面来证得平面平面.
(2)建立空间直角坐标系,利用向量法求得二面角的余弦值,进而求得其大小.
【详解】(1)连接,由三棱柱为直三棱柱可得平面,
平面,所以,
因为,,,平面,所以平面,
因为平面,所以,
因为,所以四边形是正方形,所以,
又因为,,平面,所以平面,
因为平面,所以平面平面.
(2)因为,,,根据勾股定理可知:,
从而有:,,两两垂直,以为原点,分别以,,所在直线为轴,
轴,轴建立空间直角坐标系,如图所示:
则,,,,
设平面的法向量为,因为,,
则,,
令,则,
设平面的法向量为,因为,,
则,,令,则,
设二面角的平面角为,
根据几何体特征可知为锐角,
所以,
所以二面角的大小为.
21.已知函数,且.
(1)讨论函数的单调性;
(2)当时,试判断函数的零点个数.
【答案】(1)答案见解析;(2)答案见解析.
【详解】试题分析:
(1)求出导函数,根据导函数的符号的到函数的单调性;(2)将问题转化为求方程根的个数的问题处理,分离参数后转化为判断和函数的图象的公共点的个数的问题.通过分析函数的单调性得到图象的大致形状即可.
试题解析:
(1)函数的定义域为,
∵,
∴
①当时,恒成立,
所以函数在上单调递增;
②当时,
则当时,,单调递减,
当时,,单调递增.
综上所述,当时,函数在上单调递增;
当时,函数在上单调递增,在上单调递减.
(2)由题意知,函数的零点个数即方程的根的个数.
令,
则
由(1)知当时, 在递减,在上递增,
∴.
∴在上恒成立.
∴,
∴在上单调递增.
∴,.
所以当或时,函数没有零点;
当时函数有一个零点.
点睛:研究方程根的个数(函数零点的个数、两函数图象公共点的个数)时,可以通过导数研究函数的单调性、最大值、最小值、变化趋势等,并根据题目要求,画出函数图象的大致图象,通过数形结合的思想去分析问题,可以使得问题的求解有一个清晰、直观的整体展现.
22.在直角坐标系中,直线的参数方程为(为参数),以坐标原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)求直线的普通方程与曲线的直角坐标方程;
(2)已知点的直角坐标为,过点作直线的垂线交曲线于、两点(在轴上方),求的值.
【答案】(1);
(2).
【分析】(1)根据参数方程化为普通方程的方法和极坐标化为直角坐标方程的公式求解;(2)根据直线的参数方程的几何意义求解.
【详解】(1)由,消去参数得,
即直线的普通方程为;
由,得,
∵,,∴,
即曲线的直角坐标方程.
(2)直线的斜率为,则的斜率为,所以的倾斜角为,
故设直线的参数方程为(为参数),
代入,得,
设点对应的参数为,点对应的参数为,
则,且在轴上方,有,.
故,
即的值为.
23.已知函数.
(1)当时,解不等式;
(2)若存在,使得不等式成立,求实数的取值范围.
【答案】(1)
(2)
【分析】(1)当时,,分、、三种情况解不等式,综合可得出原不等式的解集;
(2)分析可知,,可得出或,则存在,使得或,利用参变量分离法可求得实数的取值范围.
【详解】(1)解:当时,.
当时,,解得,此时;
当时,,解得,此时;
当时,,解得,此时.
因此,原不等式的解集为.
(2)解:当时,由可得,即,
即或,所以,或,
即存在,使得或.
若存在使得,则,
若存在使得,则.
因此,实数的取值范围为.
2023届甘肃省张掖市某重点校高三上学期12月月考数学(理)试题(解析版): 这是一份2023届甘肃省张掖市某重点校高三上学期12月月考数学(理)试题(解析版),共20页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2023届甘肃省张掖市某重点校高三上学期11月月考数学(文)试题(解析版): 这是一份2023届甘肃省张掖市某重点校高三上学期11月月考数学(文)试题(解析版),共15页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2023届甘肃省张掖市某重点校高三上学期12月月考数学(文)试题含解析: 这是一份2023届甘肃省张掖市某重点校高三上学期12月月考数学(文)试题含解析,共18页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












