《勾股定理》复习课课件PPT

这是一份《勾股定理》复习课课件PPT，共40页。PPT课件主要包含了考点一，考点二，考点3，考点4，勾股定理的实际应用，勾股定理逆定理的应用，考点5等内容，欢迎下载使用。

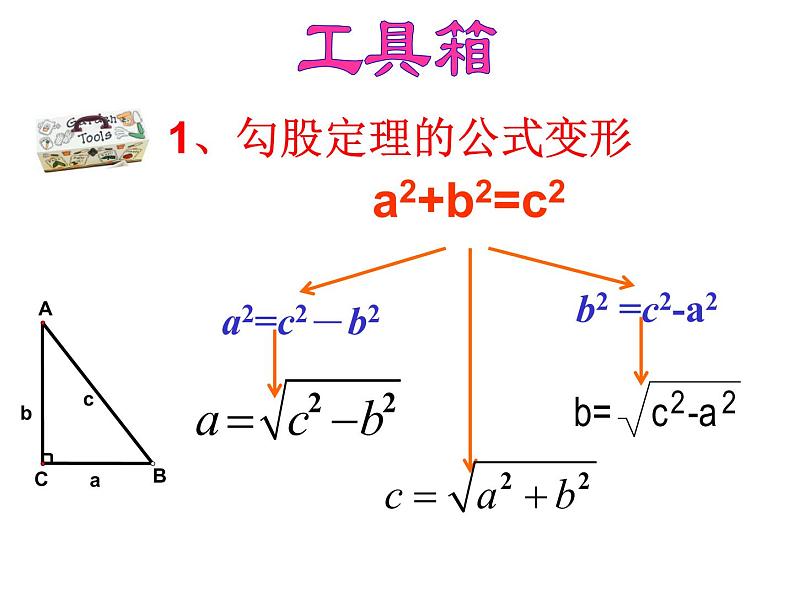
a2 + b2 = c2
直角三角形两直角边的平方和等于斜边的平方。
1、直角三角形是前提。2、谁是斜边要清楚。
1、勾股定理的公式变形
3、4、5； 5、12、13； 7、24、25； 8、15、17； 9、40、41.
满足a2 +b2=c2的三个正整数，称为勾股数
4、命题与逆命题有何关系？什么是互逆定理？
3、直角三角形中的有关定理
（1）在直角三角形中，30°角所对的直角边等于斜边的一半。
（2）在直角三角形中，一条直角边等于斜边的一半，则这条直角边所对的角为30°。
（3）直角三角形斜边上的中线等于斜边的一半。
要点1: 在两个命题中，如果第一个命题的题设是第二个命题的结论，而第一个命题的结论是第二个命题的题设，那么这两个命题叫做互逆命题．如果把其中一个命题叫做原命题，那么另一命题就叫做它的逆命题．
要点2: 每一个命题都有逆命题，只要将原命题的题设改成结论，并将结论改成题设，便可得到原命题的逆命题．但是原命题正确，它的逆命题未必正确．例如真命题“对顶角相等”的逆命题为“相等的角是对顶角”，此命题就是一个假命题．
2.勾股定理的逆定理:三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.
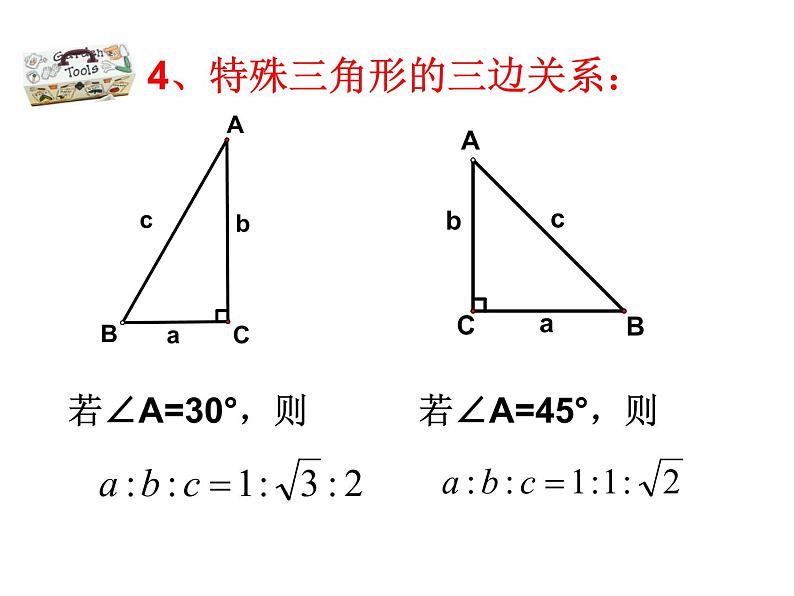
4、特殊三角形的三边关系：
与勾股定理有关的计算问题
④若∠A=30°,a=2,则c=____,b=___, a:b:c=_______;
1、在Rt△ABC中，∠C=900①若a=6，b=8， 则c=___;
②若a=40,c=41，则b=____;
S小正方形＝（b-a）2
S大正方形＝4·S三角形＋S小正方形
　　现在我们一起来回顾一下“赵爽弦图”的奥妙吧！
2、分别以直角三角形三边为半径作正方形则这三个正方形的面积S1, S2, S3之间的关系（ ）3.如图，两个正方形的面积分别为64，49，则AC=( )
S3 = S1 + S2
4、等腰三角形底边上的高为8，周长为32，求这个三角形的面积
解：设这个三角形为ABC，高为AD，设BD为x，则AB为（16-x），
由勾股定理得：x2+82=(16-x)2
即x2+64=256-32x+x2
∴ S∆ABC=BC•AD/2=2 •6 •8/2=48
2、已知Rt△ABC中，∠C=90°，若a+b=14cm， c=10cm，则Rt△ABC的面积是（　　） A、24cm2B、36cm2 C、48cm2 D、60cm2
3、直角三角形有一条直角边的长为11，另外两边的长也是正整数，则此三角形的周长是（ ）A、120 B、121 C、132 D、123
3.设另一条直角边为x，斜边为y，∵由勾股定理得：y2-x2=112，∴（y+x）（y-x）=121=11×11=121×1，∵x、y为整数，y＞x，∴x+y＞y-x，即只能x+y=121，y-x=1，解得：x=60，y=61，∴三角形的周长是11+60+61=132，故选C．
4、已知：如图，∠B=∠D=90°，∠A=60°，AB=4，CD=2。求：四边形ABCD的面积。
1、如图，铁路上A，B两点相距25km，C，D为 两村庄，DA⊥AB于A，CB⊥AB于B，已知 DA=15km，CB=10km，现在要在铁路AB上 建一个土特产品收购站E，使得C，D两村到 E站的距离相等，则E站应建在离A站多少km 处？
设AE= x km，则 BE=（25-x）km根据勾股定理，得 AD2+AE2=DE2 BC2+BE2=CE2 又 DE=CE ∴ AD2+AE2= BC2+BE2即：152+x2=102+（25-x）2 ∴ x=10 答：E站应建在离A站10km处。
与展开图形有关的计算问题
 如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短程( 取3)是( ) A.20cm;B.10cm;C.14cm;D.无法确定.
2、如图，一只蚂蚁从实心长方体的顶点A出发，沿长方体的表面爬到对角顶点C1处（三条棱长如图所示），问怎样走路线最短？最短路线长为多少？
分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.
如图5是一个三级台阶，它的每一级的长宽和高分别为20dm、3dm、2dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是 .
与勾股定理有关的证明题
如图，已知在△ABC中，∠C=90°,D为AC上一点，AB2-BD2与AC2-DC2有怎样的关系？试证明你的结论。
AB2=AC2+BC2
BD2=DC2+BC2
∴ BC2 = AB2—AC2 BC2 = BD2 — DC2
∴ AB2—AC2 = BD2 — DC2
即: AB2-BD2 = AC2-DC2
2、已知，△ABC中，AB=17cm，BC=16cm，BC边上的中线AD=15cm，试说明△ABC是等腰三角形。
提示: 先运用勾股定理证明中线AD⊥BC,再利用等腰三角形的判定方法就可以说明了.
3、如图，在△ABC中，AB=AC，P为BC上任意一点，证明：AB2－AP2=PB×PC。
解：过A点作AD⊥BC
在 Rt△ABD中,根据勾股定理,得: AB2=AD2+BD2 ①同理: AP2=AD2+DP2 ②由①-②,得 AB2－AP2=BD2-DP2 =(BD+DP)(BD-DP) =PB(BD+DP)又 AB=AC, AD⊥BC ∴ BD=CD∴ AB2－AP2=PB×PC
1、如图，要登上8米高的建筑物BC，为了安全需要，需使梯子底端离建筑物距离AB为6米，问至少需要多长的梯子？
解：根据勾股定理得：AC2= 62 + 82 =36+64 =100即：AC=10（-10不合，舍去）答：梯子至少长10米。
分析：先把实际问题转化成数学问题。
已知：AD = 0.5 尺， AC = 2尺，且∠CAB = 90º, BD =BC，求:AB的长.
1、 印度有一数学家婆什迦罗曾提出过“荷花问题”:
“平平湖水清可鉴, 面上半尺生红莲;出泥不染亭亭立, 忽被强风吹水面。渔人观看忙向前, 花离原位二尺远；能算诸君请解题， 湖水如何知深浅？”
2、如图,点A是一个半径为 ２５０ m的圆形森林公园的中心,在森林公园附近有 B .C 两个小镇,现要在 B.C 两小镇之间修一条长为 1000 m 的笔直公路将两镇连通,经测得 ∠B=60°,∠C=30°,问?请通过计算说明此公路会不会穿过该森林公园.
2、飞机在空中水平飞行，某一时刻刚好飞到一个男孩子头顶上方4千米处，过了20秒，飞机距离这个男孩子头顶5千米，飞机每小时飞行多少千米？
3.某考古员发现了一张文字叙述的藏宝图“他们登陆后先往东走8千米，又往北走2千米，遇到障碍后又往西走3千米，再折向北走到6千米处往东一拐，仅走1千米就找到宝藏”(1)请你把藏宝图画出来(2)登陆点A到宝藏点B的直线距离是多少千米？
答：登陆点A到宝藏点B的直线距离是10千米。
过点B作BC⊥AC于C
4.小刚准备测量一段河水的深度,他把一根竹竿插到离岸边15m远的水底,竹竿高出水面5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )A. 20m; B. 25m; C. 22.5m; D. 30m.
5．在一棵树的10米高处有两只猴子，一只猴子爬下树走到离树20米处的池塘的A处。另一只爬到树顶D后直接跃到A处，距离以直线计算，如果两只猴子所经过的距离相等，则这棵树高_________________________米。
如果三角形的三边长a，b，c满足a2 +b2=c2 ，那么这个三角形是直角三角形
赛一赛,看谁准 下面以a,b,c为边长的三角形是不是直角三角形？如果是那么哪一个角是直角？
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a:b: c=3:4:5 _____ _____ ;
(5)a=2m b=m2-1 c=m2+1
2、小明向东走80m后,又走了60m,再走100m回到原地,小明向东走80m后,又向 方向走的.
1、 一个零件的形状如图,量得一个零件的尺寸下: AB=3cm ,AD=4cm,BC=13cm,CD=12cm 且∠DAB=90°,你能求这个零件的面积吗?
解:在Rt△ABC中,AB=3,AD=4∴DB= 　　　＝ 5在△ＢＣＤ中，ＤＢ２＋ＤＣ２＝１６９　 ＢＣ２＝１６９∴ＤＢ２＋ＤＣ２＝ＢＣ２∴∠ＢＤＣ＝９００Ｓ＝Ｓ△ＡＢＤ+Ｓ△ＢＣＤ＝　　×３×４+ ×１２×５＝３６答：这个零件的面积为３６cm2
2、有一块菜地,形状如下, 试求它的面积.(单位:米)
6、如图，在正方形ABDC中，E是CD的中点，F为BD上一点，且BF=3FD，试猜想线段AE,EF的位置关系并证明.
解： ∠AEF=900设ＦＤ＝１则ＢＦ＝３，ＢＤ＝ＡＢ＝ＡＣ＝ＣＤ＝４ ＤＥ＝ＣＥ＝２在Ｒt△ABF中，ＡＦ２＝ＡＢ２＋ＢＰ２＝２５在Ｒt △ DEF中，ＥＦ２＝ＤＦ２＋ＤＥ２＝５在Rt △ AEC,AE2=AC2+EC2=20∴EF2+AE2=AF2∴∠AEF=900