2021-2022学年山东省东营市广饶县第一中学高一下学期4月月考数学试题（解析版）

这是一份2021-2022学年山东省东营市广饶县第一中学高一下学期4月月考数学试题（解析版），共18页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
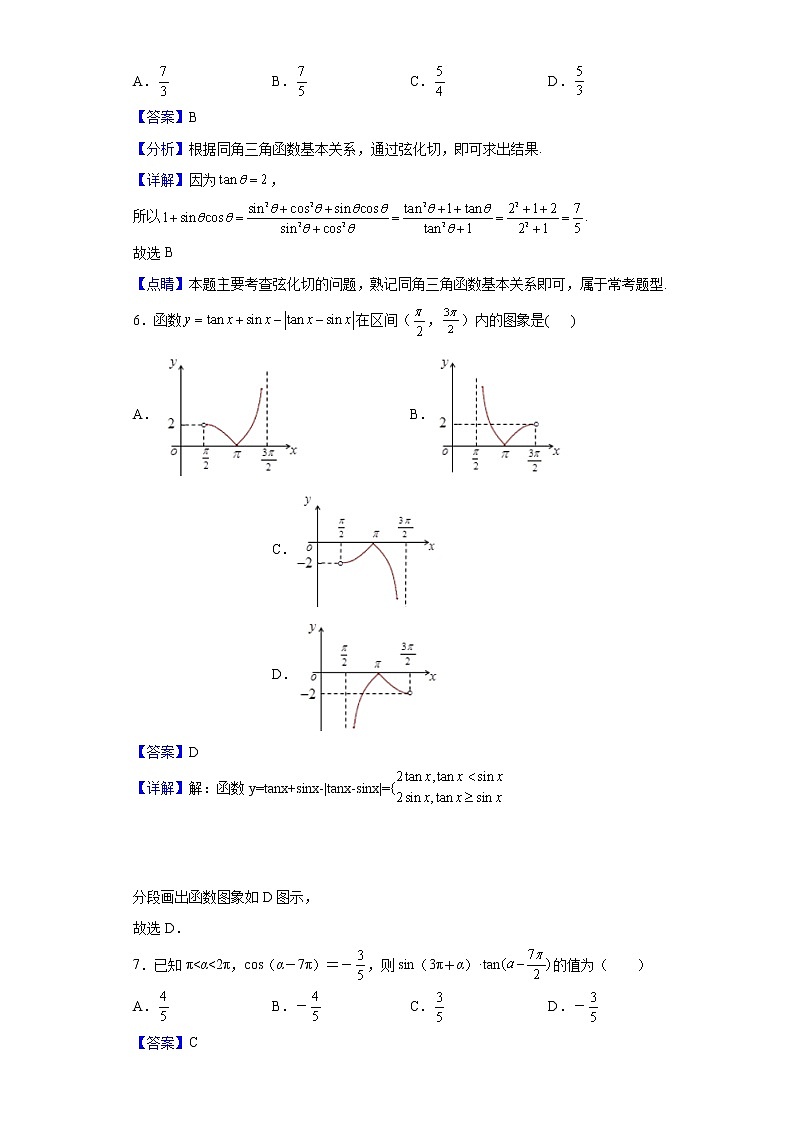
2021-2022学年山东省东营市广饶县第一中学高一下学期4月月考数学试题一、单选题1．求（       ）A． B． C． D．【答案】A【分析】由，利用诱导公式即可求解.【详解】由诱导公式可得.故选：A.2．如果点位于第三象限，那么角所在的象限是（       ）A．第一象限 B．第二象限 C．第三象限 D．第四象限【答案】B【分析】根据所给的点在第三象限，得出这个点的横坐标和纵坐标都小于零，得到角的正弦值大于零，余弦值都小于零，从而可得角是第二象限的角.【详解】点位于第三象限，，，是第二象限的角，故选：B.【点睛】本题主要考查三角函数的定义以及三角函数在象限内的符号，属于基础题.3．已知，则（       ）A． B． C． D．【答案】A【分析】将角用角表示出，再借助诱导公式变形即可.【详解】因，则，所以.故选：A4．中国折叠扇有着深厚的文化底蕴.如图（2），在半圆O中作出两个扇形OAB和OCD，用扇环形ABDC（图中阴影部分）制作折叠扇的扇面.记扇环形ABDC的面积为，扇形OAB的面积为，当与的比值为时，扇面的形状较为美观，则此时弧CD与弧AB的长度之比为（       ）A． B． C． D．【答案】B【分析】根据扇形的面积公式，求得两扇形的半径比，结合弧长公式，即可求解.【详解】设扇形的半径为，半圆半径为，，则，所以，可得，解得，则弧CD与弧AB的长度之比为.故选：B.5．如果，那么的值是A． B． C． D．【答案】B【分析】根据同角三角函数基本关系，通过弦化切，即可求出结果.【详解】因为，所以.故选B【点睛】本题主要考查弦化切的问题，熟记同角三角函数基本关系即可，属于常考题型.6．函数在区间（，）内的图象是( 　 )A． B． C． D．【答案】D【详解】解：函数y=tanx+sinx-|tanx-sinx|=   分段画出函数图象如D图示，故选D．7．已知π<α<2π，cos（α－7π）＝－，则sin（3π＋α）·tan的值为（　　）A． B．－ C． D．－【答案】C【分析】利用诱导公式和同角三角函数基本关系式求解.【详解】解：因为π<α<2π，cos（α－7π）＝－，所以,所以sin（3π＋α）·tan，，故选：C8．设函数.若对任意的实数都成立，且，在单调，则（       ）A．， B．，C．， D．，【答案】A【解析】对任意的实数都成立，可得 时函数取得最大值，则函数满足，，且在单调，再利用排除法可得答案.【详解】因为对任意的实数都成立，则时函数取得最大值，所以函数满足，，且在单调，对于A，若，，可得，，，，则在单调递增，故A符合题意；对于B，若，，可得，，故B不符合题意；对于C，若，，可得，，故C不符合题意；对于D，若，，可得，，故D不符合题意；故选：A.【点睛】方法点睛：特殊法是“小题小做”的重要策略，排除法解答选择题是高中数学一种常见的解题思路和方法，这种方法即可以提高做题速度和效率，又能提高准确性，这种方法主要适合下列题型:(1)求值问题（可将选项逐个验证）；（2）求范围问题（可在选项中取特殊值，逐一排除）；（3）图象问题（可以用函数性质及特殊点排除）；（4）解方程、求解析式、求通项、求前 项和公式问题等等.二、多选题9．下列结论正确的是（       ）A．的最小正周期是B．若圆心角为的扇形的弧长为，则该扇形面积为C．若角的终边过点，则D．若角为锐角，则角为钝角【答案】BC【分析】对于选项A：利用的最小正周期为计算即可.对于选项B：利用公式即可计算出答案.对于选项C：利用，即可计算出答案.对于选项D：当时，为直角.则可判断出答案.【详解】的周期是；A错误.若圆心角为的扇形的弧长为，则该扇形的半径为，该扇形面积为;B正确.若角的终边过点，则.C正确.当时，为直角.D错误.故选：BC.10．如图，弹簧挂着的小球做上下运动，它在时相对于平衡位置的高度单位：由关系式确定关于的函数图像如图，则下列叙述中正确的是（       ）A．函数的周期为B．函数的对称轴为C．函数的单调增区间为D．函数的图象可由函数图象上所有点的横坐标伸长为原来的倍得到【答案】ABC【分析】由题意和图象可知，，， ；结合图象可求得，，可得结合图象可求得根据周期的取值范围，根据可求得，求得根据正弦函数的图象与性质，可判定选项 A，B，C；根据图象的变换可判定选项D．【详解】由题意和图象可知，，， ．所以，即，所以或，．因为在增区间内，所以，．所以因为，所以，结合图象可知，在减区间内，所以，，解得，．根据图象可知，且，所以，所以，解得．所以，故对：，故A正确；对B：令，，解得，，所以函数的对称轴为，故 B正确；对C：令，，解得，，所以函数的单调增区间为，故C正确；对D：函数图象上所有点的横坐标伸长为原来的倍得到函数，故D错误．故选：ABC11．已知函数的图象关于直线对称，则（       ）A．函数为奇函数B．函数在上单调递增C．函数的图象向右平移个单位长度得到的函数的图象关于对称，则的最小值是D．若方程在上有2个不同实根，，则的最大值为【答案】ACD【分析】由条件可得，可得从而得出的解析式, 选项A先得出的表达式，可判断；选项B 求出函数的单调区间，可判断；选项C 根据图象平移变换得出解析式，可得答案；选项D 作出函数的图像，根据图象可判断.【详解】根据条件可得，所以则，由，所以所以选项A. 为奇函数，故A正确.选项B.   由当时，，所以函数在上单调递减，故选项B不正确.选项C. 函数的图象向右平移个单位长度得到, 根据条件可得当时，所以,则由，则当时，有的最小值是，故C正确.选项D. 作出的图象，如图当时，由，可得 由，当时，由，可得 当时，方程在上有2个不同实根，，则设，则，如图当时，，分别为，时，最大，最大值为，故D正确.故选：ACD【点睛】关键点睛：本题考查三角函数的图像性质，考查三角函数的图象变换，解答本题的关键是根据正弦型函数的对称性求出的值，根据三角函数的对称性得到，，属于中档题.12．已知函数为函数零点，直线为函数的对称轴，且在上单调，则不可能等于（       ）A．11 B．9 C．8 D．6【答案】ACD【分析】根据为函数零点及直线为函数的对称轴，则，，化简得到，再由在上单调，则，即，再逐项验证.【详解】因为为函数零点，所以，又因为直线为函数的对称轴，所以，所以，又在上单调，则，即，当时，，∵，∴，此时在上不单调，不满足题意；当时，，∵，∴，此时在上单调，满足题意；故的最大值为9，则不可能等于11，6，8，故选：ACD.【点睛】方法点睛：(1)研究f(x)＝Asin(ωx＋φ)(ω≠0)的对称轴，只需令ωx＋φ＝＋kπ(k∈Z)即可；（2）研究f(x)＝Asin(ωx＋φ)(ω≠0)的对称中心的横坐标，只需令ωx＋φ＝kπ(k∈Z)即可．（3）研究f(x)＝Asin(ωx＋φ)(ω≠0) 的单调性，只需把ωx＋φ看作一个整体代入y＝sin x的相应单调区间内即可，对于已知函数的单调区间的某一部分确定参数ω的范围的问题，首先，明确已知的单调区间应为函数的单调区间的子集，其次，要确定已知函数的单调区间，从而利用它们之间的关系可求解，另外，若是选择题利用特值验证排除法求解更为简捷．三、填空题13．化简为__________．【答案】1【分析】根据同角三角函数的基本关系式对所求表达式进行化简，由此求得表达式的值.【详解】解：依题意．故答案为：1．14．设函数的部分图象如图所示．则__________．【答案】【分析】由函数的图象求出即可求得值,代入解析式即可求得,进而求得结果.【详解】由图可知,再根据,又,所以,因此.故答案为: .【点睛】已知函数的图象求解析式.（1）;（2）由函数的周期,求;（3）利用“五点法“中相对应的特殊点求.15．已知且，则__________．【答案】【解析】根据且，利用平方关系得到及x的范围，再利用平分关系求解.【详解】因为且，所以，所以，，故答案为：16．函数y＝lg(2sinx－1)＋的定义域为__________________.【答案】【分析】要使函数有意义，则有，由三角函数线可得不等式组的解集，即得原函数的定义域.【详解】要使原函数有意义，必须有即，如图，在单位圆中作出相应的三角函数线，由图可知，解集为,取交集可得原函数的定义域为 故答案为： 【点睛】本题考查函数定义域的求解，考查利用三角函数线解不等式，属于基础题.四、解答题17．如图，在平面直角坐标系中，角的始边与x轴的非负半轴重合且与单位圆相交于点，它的终边与单位圆相交于x轴上方一点B，始边不动，终边在运动.(1)若点B的横坐标为，求的值和与角终边相同的角的集合；(2)若，请写出弓形AB的面积S与的函数关系式（注：弓形是指在圆中由弦及其所对的弧组成的图形）.附：.【答案】(1)；(2)，【分析】（1）若点的横坐标为，根据题意求出的纵坐标，从而求得的值．确定角，写出与角终边相同的角的集合．（2）若，根据弓形的面积，计算求得结果．【详解】(1)在平面直角坐标系中，角的始边与轴的非负半轴重合且与单位圆相交于点， 它的终边与单位圆相交于轴上方一点，始边不动，终边在运动，若点的横坐标为，可得的坐标为，，于是 ，与角终边相同的角的集合为 ;(2)的高为 ， ，故 ，故弓形的面积，．18．已知α为第三象限角，．(1)化简；(2)若，求．【答案】(1)=(2)【分析】（1）由诱导公式化简；（2）由诱导公式化简已知式得，再由平方关系求得即可得．【详解】(1)(2)∵   ∴ ， ∵   α是第三象限角   ∴19．设，函数．（1）求在R上的单调增区间；（2）在给定坐标系中作出函数在上的图象．【答案】（1）；（2）图见解析.【分析】（1）由条件根据余弦函数的单调性即可求解．（2）由条件利用五点法作函数函数在一个周期上的简图．【详解】解：（1）由于，函数，令，解得，可得函数的单调递增区间是．（2），列表如下：0x0100 作图：20．设函数.(1)求函数的最小正周期和对称轴方程；(2)求函数在上的最大值与最小值及相对应的x的值.【答案】(1) ；，．(2)的最大值是2，此时，的最小值是-1，此时．【分析】（1）由题意利用正弦函数的周期性和图象的对称性，得出结论．（2）由题意确定，利用正弦函数的性质，得出结论．【详解】(1)函数的最小正周期为，由，可得，，所以函数的图象对称轴方程为，．(2)由（1）知，在上，，，故当，即时，取得最大值为2，当，即时，取得最小值为-1，故的最大值是2，此时，的最小值是-1，此时．21．已知某地一天从时的温度变化曲线近似满足函数.（1）求该地区这一段时间内温度的最大温差.（2）若有一种细菌在到之间可以生存，则在这段时间内，该细菌最多能存活多长时间？【答案】（1）20；（2）（小时）.【分析】（1）利用三角函数的性质求函数在的最大值与最小值可得最大温差.（2）令，解不等式，确定解在的区间长度.【详解】（1）由函数易知，当函数取得最大值时 ，解得，又，所以当时，函数取得最大值，此时最高温度为，当函数取得最小值时 ，解得，当时，函数取得最小值，此时最低温度为，所以最大温差为.（2）解法1：令，得，因为，所以.令，得.因为，所以.故该细菌能存活的最长时间为（小时）.解法2：令，，，即，,又，取得，故该细菌能存活的最长时间为.【点睛】本题考查三角函数的性质及应用，利用三角函数图像及周期性解简单三角不等式，考查运算求解能力,属于中档题.22．已知函数的图像两相邻对称轴之间的距离是.若将的图像先向右平移个单位长度，再向上平移个单位长度，图像对应的函数为奇函数.(1)求的解析式；(2)求图像的对称轴及的单调区间；(3)若对任意，恒成立，求实数m的取值范围.【答案】(1)(2)对称轴为直线，，增区间为，减区间为(3)【分析】（1）由正弦函数的周期公式求得，再根据函数是奇函数求得b，得函数的解析式；（2）令，，，，，，分别求解可得答案；（3）根据正弦函数的性质求得.再将问题转化为恒成立.令，，由函数的单调性求得的范围，由此求得的范围.【详解】(1)解：因为，所以，所以.又因为为奇函数，且，所以且，又，所以，，所以.(2)解：令，，得；令，，得；令，，得，.所以函数图像的对称轴为直线，.函数的增区间为，减区间为.(3)解：因为，所以，所以，所以，所以.要使恒成立，即恒成立.令，，则在上单调递增，又，得，即，所以，即m的取值范围是.