2022-2023学年广东省兴宁市齐昌中学高一上学期期中数学试题（解析版）

这是一份2022-2023学年广东省兴宁市齐昌中学高一上学期期中数学试题（解析版），共11页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．已知集合，，则（ ）
A．B．C．D．
【答案】C
【分析】直接根据交集的定义计算可得；
【详解】因为，
所以
故选：C
2．设函数，则（ ）
A．B．C．3D．7
【答案】D
【分析】将代入解析式求函数值即可.
【详解】.
故选：D.
3．设 为非零实数，则下列运算正确的是（ ）
A．B．
C．D．
【答案】B
【分析】举反例可判断A;根据指数幂的运算法则一一判断B,C,D，可得答案.
【详解】对于A,当n取偶数，时不成立，比如 ，故A错误；
对于B，，正确；
对于C, ，B错误；
对于D, ,D错误，
故选：B
4．已知，则“”是“”的（ ）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
【答案】A
【分析】根据充分条件、必要条件的定义，利用基本不等式定理与举特例判断可得．
【详解】解：当时，有；
当时，有成立，
综上，“”是“”的充分不必要条件，
故选：A．
5．已知是上的奇函数，且当时，，若，则（ ）
A．B．C．D．
【答案】C
【分析】由奇函数性质有，结合已知条件及函数解析式求参数a，再利用奇函数性质求的值.
【详解】由题设，则，故，
所以时，，
则.
故选：C
6．已知函数，则不等式的解集为（ ）
A．B．C．D．
【答案】B
【分析】由分段函数表达式，判断其单调性，利用单调性，求解不等式．
【详解】根据题目所给的函数解析式，可知函数在上是减函数，
所以，解得．
故选：B
7．定义集合的一种运算：，若，，则中的元素个数为（ ）
A．B．C．D．
【答案】C
【分析】根据集合的新定义确定集合中的元素.
【详解】因为，，，
所以，
故集合中的元素个数为3，
故选：C.
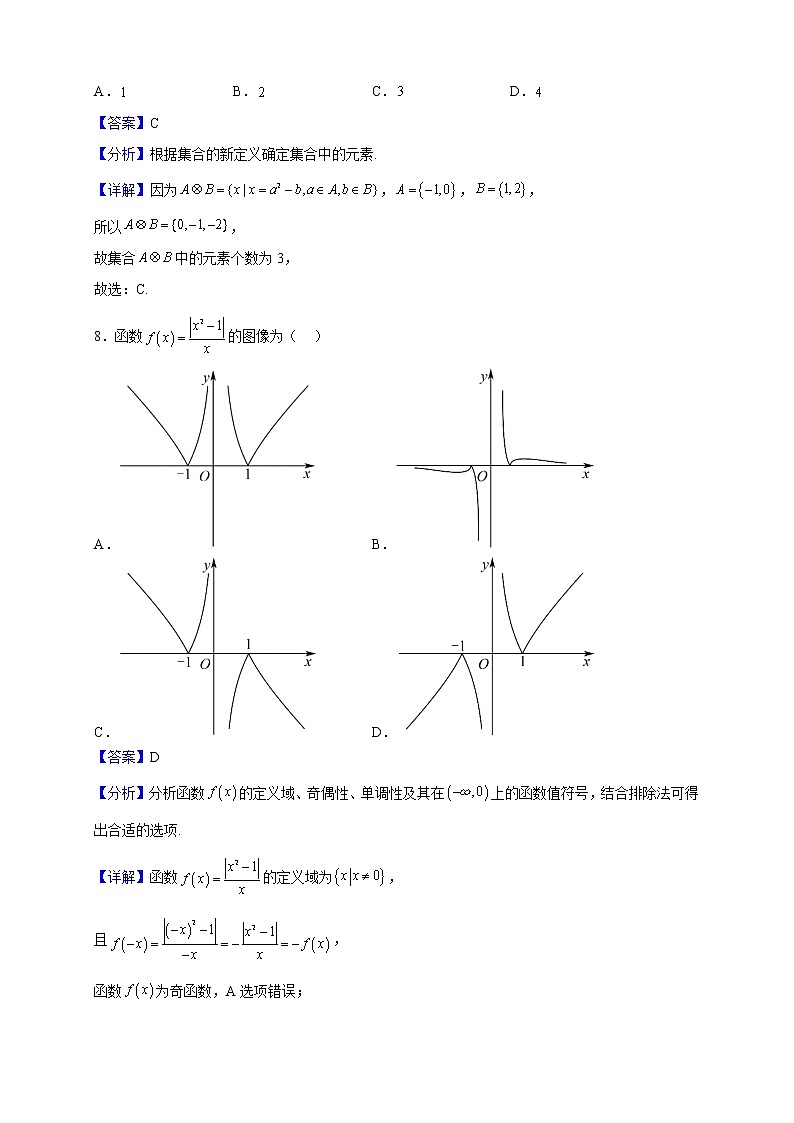
8．函数的图像为（ ）
A．B．
C．D．
【答案】D
【分析】分析函数的定义域、奇偶性、单调性及其在上的函数值符号，结合排除法可得出合适的选项.
【详解】函数的定义域为，
且，
函数为奇函数，A选项错误；
又当时，，C选项错误；
当时，函数单调递增，故B选项错误；
故选：D.
二、多选题
9．下列函数既是偶函数又在上单调递增的是（ ）
A．B．C．D．
【答案】AD
【分析】结合函数的奇偶性、单调性确定正确选项.
【详解】A选项，的定义域为，，为偶函数.
当时，为增函数，符合题意.
B选项，的定义域为，当时，为减函数，不符合题意.
C选项，的定义域为，，为奇函数，不符合题意.
D选项， 的定义域为，，为偶函数.
当时，根据复合函数单调性同增异减可知：为增函数，符合题意.
故选：AD
10．对于实数，下列结论正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则
【答案】BCD
【分析】根据不等关系对选项一一分析即可.
【详解】对于A，当时，，故A错误；
对于B，若，则，故B正确；
对于C，若，则，故C正确；
对于D，若，则 ，从而有，故正确.
故选：BCD
11．已知函数，则关于函数的结论正确的是（ ）
A．的定义域为RB．的值域为
C．D．若，则x的值为
【答案】BD
【分析】对A根据解析式判断定义域，对B结合单调性求出值域，对C代值即可求出，对D利用函数值分段讨论求出.变量的值.
【详解】由题意知函数的定义域为，故A错误；
当时，的取值范围是，当时，的取值范围是，因此的值域为，故B正确；
当时，，故C错误；
当时，，当时，，
故D正确；
故选：BD.
12．下列说法正确的是（ ）
A．命题“，都有”的否定是“，使得”
B．当时，的最小值是5
C．若不等式的解集为，则
D．函数（，）过定点
【答案】BCD
【分析】对A，根据全称命题的否定判断即可；
对B，根据基本不等式求解即可；
对C，根据二次不等式根与系数的关系求解即可；
对D，结合指数函数的性质，令，代入求解即可.
【详解】对A，命题“，都有”的否定是“，使得”，故A错误；
对B，当时，，当且仅当，即时，等号成立，故B正确；
对C，由不等式的解集为，
可知，，所以，，则，故C正确；
对D，令，则，所以，所以函数过定点，故D正确；
故选：BCD
三、填空题
13．_____
【答案】4
【分析】根据分数指数幂的运算性质计算即可
【详解】
故答案为：4
14．若幂函数的图像关于y轴对称，则实数______．
【答案】
【分析】根据幂函数的概念和性质计算即可
【详解】由幂函数可得，解得或，
又因为函数图像关于y轴对称，则a为偶数，所以．
故答案为：
15．已知函数的定义域为，且函数为奇函数，若，则______.
【答案】
【分析】根据函数为奇函数求出即可得解.
【详解】解：因为函数为奇函数，
所以，
即，
所以.
故答案为：.
16．已知函数的值域为，则实数的取值范围为___________.
【答案】
【分析】由题意可得，计算不等式组即可求得结果.
【详解】∵函数的值域为，又当时，，
∴，解得.
故答案为：.
四、解答题
17．(1)已知，求的解析式；
(2)已知，求的解析式．
【答案】(1)
(2)
【分析】（1）通过换元，令，从而得到的解析式；
（2）通过令为，从而得到，列出关于和的方程组，从而得到的解析式.
【详解】（1）令 ，则
所以
即
（2）因为
所以
即
所以
18．已知函数（，且）满足.
(1)求的值；
(2)解不等式.
【答案】(1)
(2)
【分析】（1）根据解析式及题中所给数据，代入即可得a值
（2）由（1）可得解析式，代入不等式，根据指数的运算性质即单调性，即可得答案.
【详解】（1）因为
所以，整理得，解得或（舍）
（2）由（1）可得，
所以，即为，整理可得，
因为为单调递增函数，
所以，解得，
所以不等式的解集为
19．已知二次函数．
(1)当时，二次函数取得最小值0，求二次函数的解析式．
(2)在（1）的条件下，恒成立，求的范围．
【答案】(1)
(2)
【分析】（1）利用二次函数的对称轴以及最值可求解；
（2）恒成立即可求解.
【详解】（1）依题意得
解得，
（2）由（1），得，则恒成立，
即恒成立，
只需的最小值大于即可
，
的最小值是
的取值范围：
20．已知是定义在上的偶函数，且时，．
(1)求函数的表达式；
(2)判断并证明函数在区间上的单调性．
【答案】(1)
(2)单调减函数，证明见解析
【分析】（1）设，则，根据是偶函数，可知，然后分两段写出函数解析式即可；
（2）利用函数单调性的定义，即可判断函数的单调性，并可证明结果．
【详解】（1）解：设，则，，
因为函数为偶函数，所以，即，
所以．
（2）解：设，，
∵，∴，，
∴，∴在为单调减函数．
21．若函数在区间上有最大值4和最小值1，设．
(1)求a、b的值；
(2)若不等式在上有解，求实数k的取值范围；
【答案】(1)
(2)
【分析】（1）由二次函数在上的单调性最大值和最小值，从而求得；
（2）用分离参数法化简不等式为，然后令换元，转化为求二次函数的最值，从而得参数范围．
【详解】（1），对称轴，
在上单调递增，
所以，解得；
（2）由（1）知化为，
即，
令，则，因为，所以，
问题化为，
记，对称轴是，因为，所以，
所以．
22．某研究所开发了一种抗病毒新药，用小白鼠进行抗病毒实验．已知小白鼠服用1粒药后，每毫升血液含药量（微克）随着时间（小时）变化的函数关系式近似为．当每毫升血液含药量不低于4微克时，该药能起到有效抗病毒的效果．
(1)若小白鼠服用1粒药，多长时间后该药能起到有效抗病毒的效果？
(2)某次实验：先给小白鼠服用1粒药，6小时后再服用1粒，请问这次实验该药能够有效抗病毒的时间为多少小时？
【答案】(1)小时
(2)小时
【分析】（1）根据，代入第一段解析式中求不等式即可.（2）根据分段函数的函数值要不低于4，分段求解即可.
【详解】（1）设服用1粒药，经过小时能有效抗病毒，
即血液含药量须不低于4微克，可得，
解得，
所以小时后该药能起到有效抗病毒的效果．
（2）设经过小时能有效抗病毒，即血液含药量须不低于4微克；
若，药物浓度，
解得，
若，药物浓度，
化简得，所以；
若，药物浓度，
解得，所以；
综上，
所以这次实验该药能够有效抗病毒的时间为小时．