

初中数学北师大版八年级下册第一章 三角形的证明2 直角三角形精品同步训练题
展开一、选择题
1.下列各组数为勾股数的是( )
A.6,12,13 B.3,4,7 C.4,7.5,8.5 D.8,15,16
2.以下列线段a,b,c的长为三角形的三边长,不能构成直角三角形的是( )
A.a=9,b=41,c=40 B.a=5,b=5,c=5eq \r(2)
C.a∶b∶c=3∶4∶5 D.a=11,b=12,c=15
3.如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,边长为无理数的边数是( )
A.0 B.1 C.2 D.3
4.直角三角形的两边长分别是6,8,则第三边的长为( )
A.10 B.2eq \r(2) C.10或2eq \r(7) D.无法确定
5.已知一个直角三角形的两直角边长分别为5和12,则第三边长的平方是( )
A.169 B.119 C.13 D.144
6.有下面的判断:
①若△ABC中,a2+b2≠c2,则△ABC不是直角三角形;
②△ABC是直角三角形,∠C=90°,则a2+b2=c2;
③若△ABC中,a2﹣b2=c2,则△ABC是直角三角形;
④若△ABC是直角三角形,则(a+b)(a﹣b)=c2.
其中判断正确的有( )
A.4个 B.3个 C.2个 D.1个
7.如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中小正方形顶点A,B在围成的正方体上的距离是( )
A.0 B.1 C.eq \r(2) D.eq \r(3)
8.如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
A.3eq \r(3) B.6 C.3eq \r(2) D.eq \r(21)
二、填空题
9.一个正方形的面积是5,那么这个正方形的对角线的长度为 .
10.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c.
(1)若a=2,b=4,则c=__________;
(2)若a=2,c=4,则b=__________;
(3)若c=26,a︰b=5︰12,则a=__________,b=__________.
11.已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别4cm2和15cm2,则正方形③的面积为 .
12.如图,正方形的边长是1个单位长度,则图中B点所表示的数是 ;若点C是数轴上一点,且点C到A点的距离与点C到原点的距离相等,则点C所表示的数是 .
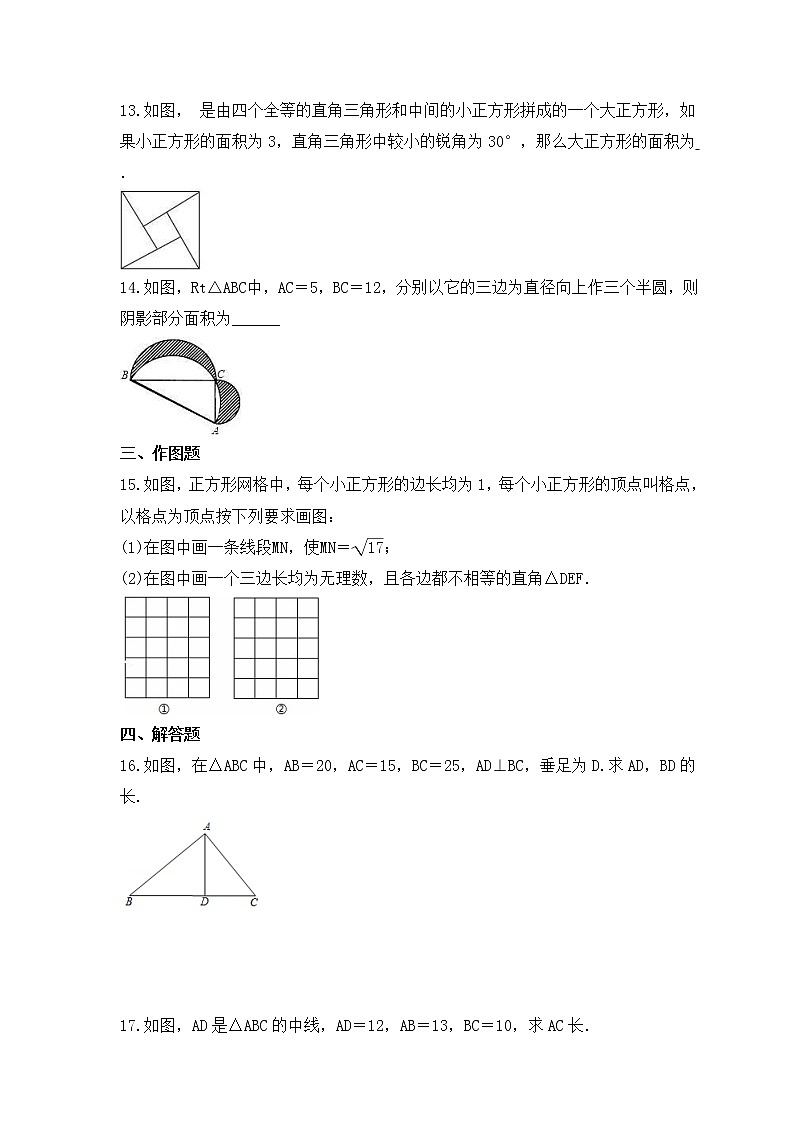
13.如图, 是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如果小正方形的面积为3,直角三角形中较小的锐角为30°,那么大正方形的面积为 .
14.如图,Rt△ABC中,AC=5,BC=12,分别以它的三边为直径向上作三个半圆,则阴影部分面积为______
三、作图题
15.如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点,以格点为顶点按下列要求画图:
(1)在图中画一条线段MN,使MN=eq \r(17);
(2)在图中画一个三边长均为无理数,且各边都不相等的直角△DEF.
四、解答题
16.如图,在△ABC中,AB=20,AC=15,BC=25,AD⊥BC,垂足为D.求AD,BD的长.
17.如图,AD是△ABC的中线,AD=12,AB=13,BC=10,求AC长.
18.一根垂直于地面的电线杆AC=8m,因特殊情况,在点B处折断,顶端C落在地面上的C′处,测得AC′的长是4m,求底端A到折断点B的长.
19.A、B两个村庄在笔直的小河CD的同侧,A、B两村到河的距离分别为AC=1千米,BD=3千米,CD=3千米.现要在河边CD上建一水厂向A、B两村输送自来水,铺设管道的工程费用为每千米2万元.请你在CD上选择水厂的位置并作出点O,使铺设水管的费用最节省,并求出铺设水管的总费用.
20.如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?
参考答案
1.D
2.D.
3.D
4.C
5.A
6.C
7.B
8.A.
9.答案为:eq \r(10).
10.答案为:(1)2eq \r(5);(2)2eq \r(3);(3)10,24.
11.答案为:19.
12.答案为:﹣eq \r(2);eq \f(\r(2),2).
13.答案为:12+6eq \r(3).
14.答案为:30;
15.解:如图所示:
16.解:∵AB2+AC2=202+152=625=252=BC2,
∴△ABC是直角三角形,
∵S△ACB=eq \f(1,2)×AB×AC=eq \f(1,2)×BC×AD,
∴15×20=25×AD,
∴AD=12,
由勾股定理得BD=16.
17.解:∵AD是△ABC的中线,且BC=10,
∴BD=eq \f(1,2)BC=5.
∵52+122=132,即BD2+AD2=AB2,
∴△ABD是直角三角形,则AD⊥BC,
又∵CD=BD,
∴AC=AB=13.
18.解:设电线杆底端A到折断点B的长为x米,
则斜边为(8﹣x)米,
根据勾股定理得:x2+42=(8﹣x)2
解得:x=3.
故底端A到折断点B的长为3m.
19.解:依题意,只要在直线l上找一点O,使点O到A、B两点的距离和最小.
作点A关于直线l的对称点A′,连接A′B,
则A′B与直线l的交点O到A、B两点的距离和最小,且OA+OB=OA′+OB=A′B.
过点A′向BD作垂线,交BD的延长线于点E,
在Rt△A′BE 中,A′E=CD=3,BE=BD+DE=4,
根据勾股定理可得:A′B=5(千米)
即铺设水管长度的最小值为5千米.
所以铺设水管所需费用的最小值为:5×2=10(万元).
20.解:(1)由A点向BF作垂线,垂足为C,
在Rt△ABC中,∠ABC=30°,AB=320km,则AC=160km,
因为160<200,所以A城要受台风影响;
(2)设BF上点D,DA=200千米,则还有一点G,有AG=200千米.
因为DA=AG,所以△ADG是等腰三角形,
因为AC⊥BF,所以AC是DG的垂直平分线,CD=GC,
在Rt△ADC中,DA=200千米,AC=160千米,
由勾股定理得,CD=120千米,则DG=2DC=240千米,
遭受台风影响的时间是:t=240÷40=6(小时).
初中北师大版2 直角三角形习题: 这是一份初中北师大版<a href="/sx/tb_c94876_t7/?tag_id=28" target="_blank">2 直角三角形习题</a>,共6页。试卷主要包含了2 直角三角形同步练习等内容,欢迎下载使用。
初中数学北师大版八年级下册2 直角三角形课后测评: 这是一份初中数学北师大版八年级下册2 直角三角形课后测评,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学北师大版八年级下册2 直角三角形精练: 这是一份初中数学北师大版八年级下册2 直角三角形精练,共6页。试卷主要包含了下列说法正确的有,下列三个定理存在逆定理的有,如图,是上一点,,则的长为等内容,欢迎下载使用。













