






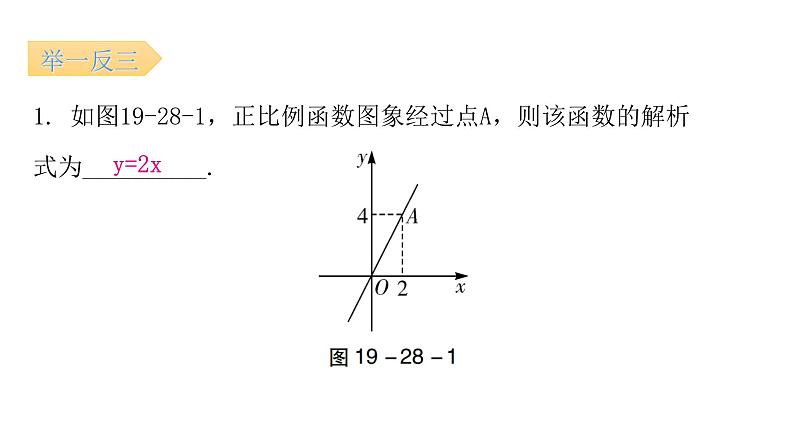
所属成套资源:全套人教版八年级数学下册课时教学课件
人教版八年级下册19.2.2 一次函数教课ppt课件
展开
这是一份人教版八年级下册19.2.2 一次函数教课ppt课件,共23页。PPT课件主要包含了第十九章一次函数,本章知识梳理等内容,欢迎下载使用。
第28课时 一次函数(二)
1. 能利用待定系数法求一次函数解析式. 2. 体会一次函数与二元一次方程的关系.
知识点:用待定系数法求一次函数的解析式先设出函数__________,再根据条件确定解析式中__________________ ,从而得出函数解析式的方法,叫做待定系数法.
【例1】若正比例函数的图象经过点(-4,2),则它的解析式为______________.思路点拨:利用待定系数法求解即可.
【例2】已知一次函数的图象经过点(4,6)和(1,3). (1)求此一次函数的表达式;(2)若点(a,5)在函数图象上,求a的值.
(2)∵点(a,5)在该函数的图象上,∴a+2=5. 解得a=3.
思路点拨:(1)利用待定系数法求解即可;(2)把点(a,5)代入一次函数的解析式,解方程即可.
(2)证明:在y=x+2中,令y=0,则x=-2;令x=0,则y=2. ∴C(-2,0),D(0,2). ∴OC=2,OD=2. ∴OC=OD.
【例3】已知直线y=kx+b的平行于直线y=2x,且经过点(0,3),求该直线的解析式. 思路点拨:先根据直线平行可得k的值,再将点(0,3)代入求出b的值,即可得到直线的解析式.
解:∵直线y=kx+b平行于直线y=2x,∴k=2. 将点(0,3)代入y=2x+b,得b=3. ∴该直线的解析式为y=2x+3.
【例4】已知y与x-2成正比例,且当x=3时,y=2. (1)求y与x之间的函数关系式;(2)当y=-2时,求自变量x的值.
解:(1)设y=k(x-2)(k≠0). 将x=3,y=2代入,得2=(3-2)k. 解得k=2. ∴y与x之间的函数关系式为y=2x-4. (2)当y=-2时,得-2=2x-4. 解得x=1.
思路点拨:(1)利用待定系数法求解即可;(2)将y=-2代入关系式计算即可.
4. 已知y-1与x+2成正比例,且当x=-1时,y=3. (1)求y与x之间的函数关系式;(2)若点(2m+1,-1)是该函数图象上的一点,求m的值.
解:(1)设y-1=k(x+2)(k≠0). 把x=-1,y=3代入,得3-1=(-1+2)k. 解得k=2. ∴y与x之间的函数关系式为y=2(x+2)+1=2x+5. (2)把点(2m+1,-1)代入y=2x+5,得-1=2(2m+1)+5. 解得m=-2.
思路点拨:先求出点B的坐标,再利用待定系数法求解即可.
相关课件
这是一份数学19.2.2 一次函数多媒体教学课件ppt,共7页。PPT课件主要包含了课堂8分钟,第十九章一次函数,核心知识当堂测等内容,欢迎下载使用。
这是一份人教版19.2.2 一次函数说课ppt课件,共13页。PPT课件主要包含了分层作业本,第十九章一次函数等内容,欢迎下载使用。
这是一份初中人教版19.2.2 一次函数教案配套ppt课件,共19页。PPT课件主要包含了分层作业本,第十九章一次函数等内容,欢迎下载使用。









