高中物理高考 2022年高考物理一轮复习 第7章 专题强化11 碰撞模型及拓展

这是一份高中物理高考 2022年高考物理一轮复习 第7章 专题强化11 碰撞模型及拓展，共16页。试卷主要包含了理解碰撞的种类及其遵循的规律等内容，欢迎下载使用。
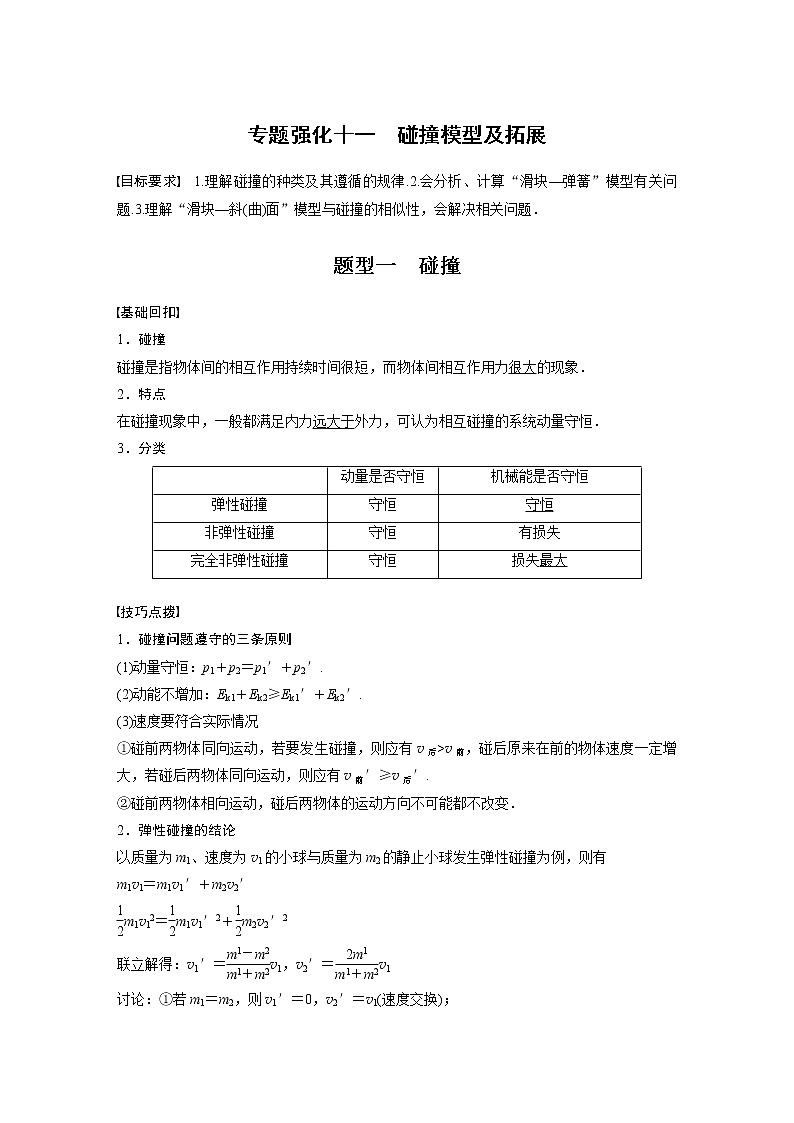
专题强化十一　碰撞模型及拓展
目标要求　1.理解碰撞的种类及其遵循的规律.2.会分析、计算“滑块—弹簧”模型有关问题.3.理解“滑块—斜(曲)面”模型与碰撞的相似性，会解决相关问题．
题型一　碰撞
基础回扣
1．碰撞
碰撞是指物体间的相互作用持续时间很短，而物体间相互作用力很大的现象．
2．特点
在碰撞现象中，一般都满足内力远大于外力，可认为相互碰撞的系统动量守恒．
3．分类

动量是否守恒
机械能是否守恒
弹性碰撞
守恒
守恒
非弹性碰撞
守恒
有损失
完全非弹性碰撞
守恒
损失最大

技巧点拨
1．碰撞问题遵守的三条原则
(1)动量守恒：p1＋p2＝p1′＋p2′.
(2)动能不增加：Ek1＋Ek2≥Ek1′＋Ek2′.
(3)速度要符合实际情况
①碰前两物体同向运动，若要发生碰撞，则应有v后>v前，碰后原来在前的物体速度一定增大，若碰后两物体同向运动，则应有v前′≥v后′.
②碰前两物体相向运动，碰后两物体的运动方向不可能都不改变．
2．弹性碰撞的结论
以质量为m1、速度为v1的小球与质量为m2的静止小球发生弹性碰撞为例，则有
m1v1＝m1v1′＋m2v2′
m1v12＝m1v1′2＋m2v2′2
联立解得：v1′＝v1，v2′＝v1
讨论：①若m1＝m2，则v1′＝0，v2′＝v1(速度交换)；
②若m1>m2，则v1′>0，v2′>0(碰后两物体沿同一方向运动)；当m1≫m2时，v1′≈v1，v2′≈2v1；
③若m1M，第一次碰撞后，A与C速度同向，且A的速度小于C的速度，不可能与B发生碰撞；如果m＝M，第一次碰撞后，A停止，C以A碰前的速度向右运动，A不可能与B发生碰撞，所以只需考虑mm2，m2的左边有一固定挡板．由图示位置静止释放m1、m2，当m1与m2相距最近时m1的速度为v1，则在以后的运动过程中(　　)

图4
A．m1的最小速度是0
B．m1的最小速度是v1
C．m2的最大速度是v1
D．m2的最大速度是v1
答案　BD
解析　由题意结合题图可知，当m1与m2相距最近时，m2的速度为0，此后，m1在前，做减速运动，m2在后，做加速运动，当再次相距最近时，m1减速结束，m2加速结束，因此此时m1速度最小，m2速度最大，在此过程中系统动量和机械能均守恒，m1v1＝m1v1′＋m2v2，m1v12＝m1v1′2＋m2v22，解得v1′＝v1，v2＝v1，B、D选项正确．
例3　如图5所示，一轻质弹簧的一端固定在滑块B上，另一端与滑块C接触但未连接，该整体静止放在离地面高为H＝5 m的光滑水平桌面上．现有一滑块A从光滑曲面上离桌面h＝1.8 m高处由静止开始滑下，与滑块B发生碰撞并粘在一起压缩弹簧推动滑块C向前运动，经一段时间，滑块C脱离弹簧，继续在水平桌面上匀速运动一段后从桌面边缘飞出．已知mA＝1 kg，mB＝2 kg，mC＝3 kg，取g＝10 m/s2.求：

图5
(1)滑块A与滑块B碰撞结束瞬间的速度大小；
(2)被压缩弹簧的最大弹性势能；
(3)滑块C落地点与桌面边缘的水平距离．
答案　(1)2 m/s　(2)3 J　(3)2 m
解析　(1)滑块A从光滑曲面上h高处由静止开始滑下的过程机械能守恒，设其滑到底面的速度为v1，由机械能守恒定律有mAgh＝mAv12，解得v1＝6 m/s
滑块A与B碰撞的过程，A、B系统的动量守恒，碰撞结束瞬间具有共同速度，设为v2，由动量守恒定律有
mAv1＝(mA＋mB)v2，
解得v2＝v1＝2 m/s
(2)滑块A、B发生碰撞后与滑块C一起压缩弹簧，压缩的过程机械能守恒，被压缩弹簧的弹性势能最大时，滑块A、B、C速度相等，设为v3，由动量守恒定律有
mAv1＝(mA＋mB＋mC)v3，
解得v3＝v1＝1 m/s
由机械能守恒定律有
Ep＝(mA＋mB)v22－(mA＋mB＋mC)v32
解得Ep＝3 J
(3)被压缩弹簧再次恢复自然长度时，滑块C脱离弹簧，设滑块A、B的速度为v4，滑块C的速度为v5，由动量守恒定律和机械能守恒定律有
(mA＋mB)v2＝(mA＋mB)v4＋mCv5
(mA＋mB)v22＝(mA＋mB)v42＋mCv52
解得v4＝0，v5＝2 m/s
滑块C从桌面边缘飞出后做平抛运动s＝v5t，H＝gt2
解得s＝2 m.

　　　　　 “滑块—斜(曲)面”模型

1．模型图示

2．模型特点
(1)最高点：m与M具有共同水平速度v共，m不会从此处或提前偏离轨道．系统水平方向动量守恒，mv0＝(M＋m)v共；系统机械能守恒，mv02＝(M＋m)v共2＋mgh，其中h为滑块上升的最大高度，不一定等于圆弧轨道的高度(完全非弹性碰撞拓展模型)
(2)最低点：m与M分离点．水平方向动量守恒，mv0＝mv1＋Mv2；系统机械能守恒，mv02＝mv12＋Mv22 (完全弹性碰撞拓展模型)

例4　(多选)如图6所示，质量为M的楔形物体静止在光滑的水平地面上，其斜面光滑且足够长，与水平方向的夹角为θ.一个质量为m的小物块从斜面底端以初速度v0沿斜面向上开始运动．当小物块沿斜面向上运动到最高点时，速度大小为v，距地面高度为h，重力加速度为g，则下列关系式中正确的是(　　)

图6
A．mv0＝(m＋M)v
B．mv0cos θ＝(m＋M)v
C．mgh＝m(v0sin θ)2
D．mgh＋(m＋M)v2＝mv02
答案　BD
解析　小物块上升到最高点时，小物块相对楔形物体静止，所以小物块与楔形物体的速度都为v，二者组成的系统在水平方向上动量守恒，全过程机械能守恒．以水平向右为正方向，在小物块上升过程中，由水平方向系统动量守恒得mv0cos θ＝(m＋M)v，故A错误，B正确；系统机械能守恒，由机械能守恒定律得mgh＋(m＋M)v2＝mv02，故C错误，D正确．
例5　(2021·黑龙江哈尔滨市第六中学期中)两质量均为m的劈A和B，高度相同，放在光滑水平面上，A和B的倾斜面都是光滑曲面，曲面下端与水平面相切，如图7所示．一质量也为m的可视为质点的物块，从劈A上距水平面高度为h处静止滑下，然后又滑上劈B.重力加速度为g，求：

图7
(1)物块在劈B上能够达到的最大高度；
(2)物块从劈B上返回水平面时的速度．
答案　(1)　(2)0
解析　(1)物块从劈A上滑下，设水平向右为正方向，物块滑到底端时的速度为v1，劈A的速度为v2.由水平方向动量守恒和系统机械能守恒列方程得
0＝mv1＋mv2
mgh＝mv12＋mv22
解得v1＝
物块滑上劈B，当二者水平方向速度相同时，物块到达最大高度．设二者共同速度大小为
v共，物块到达最大高度为H，由水平方向动量守恒和系统机械能守恒列方程得
mv1＝2mv共
mv12＝×2mv共2＋mgH
解得H＝.
(2)设物块从劈B上返回水平面时的速度为v3，劈B的速度为v4，从物块刚要滑上劈B，到物块从劈B上返回水平面，由水平方向动量守恒和系统机械能守恒列方程得：
mv1＝mv3＋mv4
mv12＝mv32＋mv42
解得v3＝0.

3．(“滑块—斜面”模型分析)如图8所示，在足够长的光滑水平面上有一静止的质量为M的斜面，斜面表面光滑、高度为h、倾角为θ.一质量为m(m