北师大版八年级下册第一章 三角形的证明1 等腰三角形一等奖ppt课件

1.1  等腰三角形（第3课时 等腰三角形的判定与反证法）

教学目标

1.理解等腰三角形的判定定理，并会运用其进行简单的证明．

2.理解反证法的基本证题思路，培养学生的逆向思维能力，并能简单应用．

教学重点难点

重点：掌握等腰三角形的判定定理．

难点：利用反证法进行证明．

教学过程

复习回顾

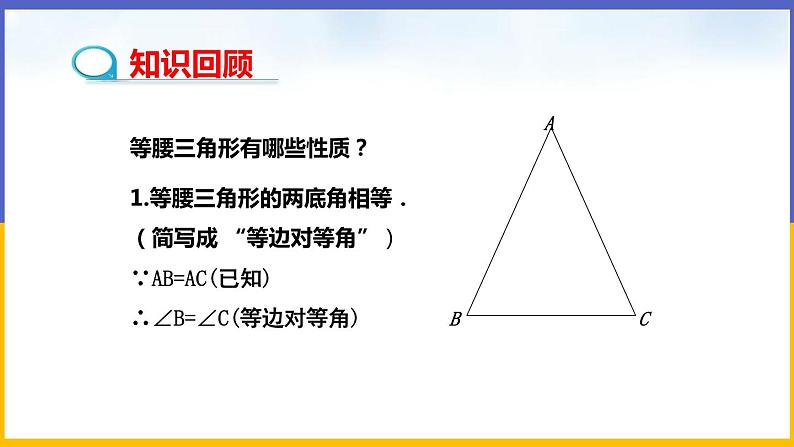
等腰三角形有哪些性质？

1.等腰三角形的两底角相等（简写成 “等边对等角”）.

2.等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合（ 简写成“三线合一” ）.

探究新知

一、预习新知

（阅读教材P8～P9的内容，回答下面问题）

1．有两个角相等的三角形是等腰三角形，简述为等角对等边．

2．先假设命题的结论不成立，然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果，从而证明命题的结论一定成立，这种证明方法称为反证法．

二、合作探究

问题1 前面已经证明了等腰三角形的两个底角相等，反过来，有两个角相等的三角形是等腰三角形吗?

已知：在△ABC中，∠B=∠C.

求证：AB=AC．

【探索】只要构造两个全等的三角形，使AB与AC成为对应边就可以了. 比如作BC的中线，或作角A的平分线，或作BC边上的高，都可以把△ABC分成两个全等的三角形．

【互动】学生完成证明过程，老师进行指导点评.

【总结】定理：有两个角相等的三角形是等腰三角形，简述为等角对等边.

例题讲解

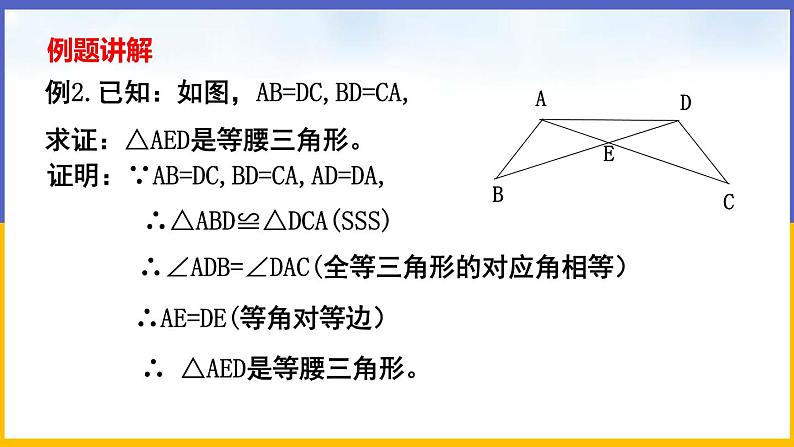
例1  已知：如图所示，AB=DC,BD=CA.

求证：△AED是等腰三角形.

证明：∵AB=DC,BD=CA,AD=DA,

∴△ABD≌△DCA(SSS).

∴∠ADB=∠DAC(全等三角形的对应角相等）.

∴AE=DE(等角对等边）.

∴ △AED是等腰三角形.

问题2  小明说，在一个三角形中，如果两个角不相等，那么这两个角所对的边也不相等．你认为这个结论成立吗?如果成立，你能证明它吗?

小明是这样想的：

   如图，在△ABC中，已知∠B≠∠C，此时AB与AC要么相等，要么不相等．

   假设AB=AC，那么根据“等边对等角”可得∠C=∠B，这与已知条件“∠B≠∠C”相矛盾，因此 AB≠AC.

【互动】你能理解他的推理过程吗?

问题3 上面小明证明问题的方法与以前的有什么不同？他的证明思路是怎样的？

【总结】（学生表述，老师引导点评）小明在证明时，先假设命题的结论不成立，然后由此推导出了与已知或公理或已证明过的定理相矛盾，从而证明命题的结论一定成立．这种证明方法称为反证法．

反证法是一种重要的数学证明方法，在解决某些问题时常常会有出人意料的效果.

    例题讲解

例2  用反证法证明：一个三角形不能有两个角是直角.

    已知：△ABC.

    求证：∠A，∠B，∠C中不能有两个角是直角.

    证明：假设∠A，∠B，∠C中有两个角是直角，

    不妨设∠A和∠B是直角，

    即∠A=90，∠B=90 ，

    于是 ∠A+∠B+∠C=90+90+∠C＞180.

    这与三角形的内角和定理矛盾，

    因此，“∠A和∠B是直角”的假设不成立.

    所以，一个三角形中不能有两个角是直角.

【总结】用反证法证题的一般步骤：

1.假设， 先假设命题的结论不成立；

2.归谬，从这个假设出发,应用正确的推理方法,得出与定义、公理、已证定理或已知条件相矛盾的结果；

3.结论: 由矛盾的结果判定假设不正确,从而肯定命题的结论正确.

三、新知应用

    例3  如图所示，在△ABC中，∠ACB＝90，CD是AB边上的高，AE是∠BAC的平分线，AE与CD交于点F.求证：△CEF是等腰三角形．

【探索】(引发学生思考)要证△CEF是等腰三角形，结合已知条件考虑证明CE＝CF即可．

证明：∵在△ABC中，∠ACB＝90，∴∠B＋∠BAC＝90.

∵CD是AB边上的高，∴∠ACD＋∠BAC＝90，∴∠B＝∠ACD.

∵AE是∠BAC的平分线，∴∠BAE＝∠EAC.

又∵∠B＋∠BAE＝∠AEC，∠ACD＋∠EAC＝∠CFE，

∴∠CEF＝∠CFE，∴ CE＝CF，∴ △CEF是等腰三角形．

【总结】(学生总结，老师点评)“等角对等边”是判定等腰三角形的重要依据，是先有角相等再有边相等，只限于在同一个三角形中，若在两个不同的三角形中，此结论不一定成立．

例4  求证：△ABC中不能有两个钝角．

证明：假设△ABC中能有两个钝角，不妨设∠A＜90，∠B＞90，∠C＞90，

所以∠A＋∠B＋∠C＞180，

这与三角形的内角和等于180矛盾，所以假设不成立.

因此原命题正确，即△ABC中不能有两个钝角．

课堂小结

(学生总结，老师点评)

1.定理：有两个角相等的三角形是等腰三角形,简述为等角对等边.

2.反证法的步骤：(1)假设结论不成立；(2)从假设出发推出矛盾；(3)假设不成立，则结论成立．

布置作业

请完成教材习题1.3

板书设计

1　等腰三角形

第3课时　等腰三角形的判定与反证法

1.定理：有两个角相等的三角形是等腰三角形，简述为等角对等边.

2.反证法的步骤：

（1）假设结论不成立；

（2）从假设出发推出矛盾；

（3）假设不成立，则结论成立.

例3  如图所示，在△ABC中，∠ACB＝90，CD是AB边上的高，AE是∠BAC的平分线，AE与CD交于点F.求证：△CEF是等腰三角形．