北师版数学八年级下册 6.1.1平行四边形的边角特征 课件

这是一份北师版数学八年级下册 6.1.1平行四边形的边角特征 课件，共23页。

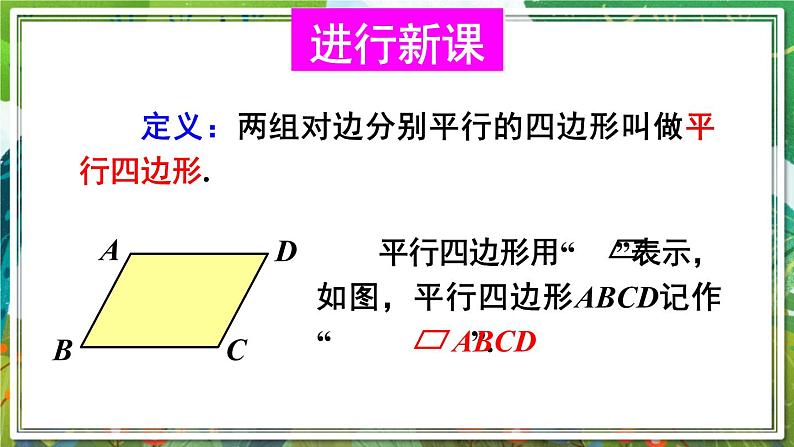
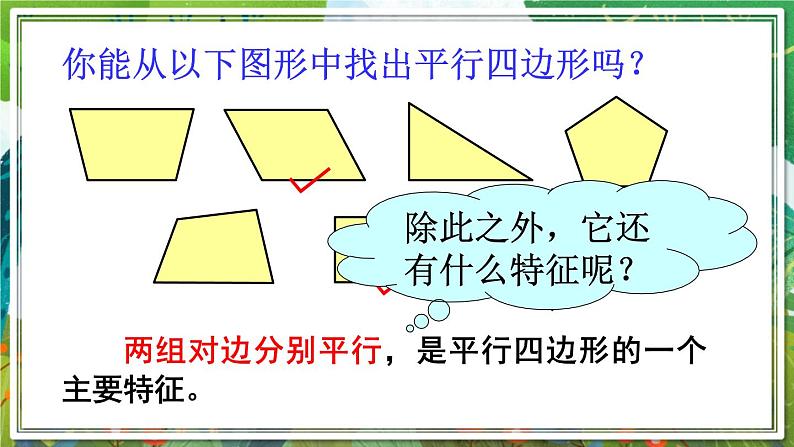
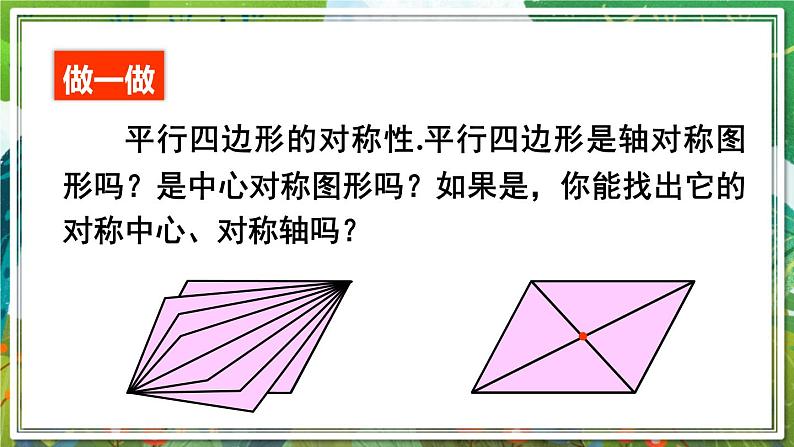
新课导入 这些都是日常生活中常见的情形，它们是否都具有相似的特征？这些物体都是什么形状？生活中的平行四边形进行新课 定义：两组对边分别平行的四边形叫做平行四边形.平行四边形的有关概念：1.平行四边形中相对的边称为对边，相对的角称为对角。2.平行四边形中相邻的边称为邻边，相邻的角称为邻角。3.平行四边形不相邻的两个顶点连成的线段叫它的对角线。如图：AC、BD.∵四边形ABCD是平行四边形（已知），∴AB∥CD，AD∥BC（平行四边形的定义）．∵AB∥CD，AD∥BC（已知），∴四边形ABCD是平行四边形（平行四边形的定义）．你能从以下图形中找出平行四边形吗？ 两组对边分别平行，是平行四边形的一个主要特征。除此之外，它还有什么特征呢？ 平行四边形的对称性.平行四边形是轴对称图形吗？是中心对称图形吗？如果是，你能找出它的对称中心、对称轴吗？做一做 平行四边形是中心对称图形，两条对角线的交点是它的对称中心.我们还发现：平行四边形的对边相等、对角相等.请你尝试证明这些结论.归纳小结已知：如图，四边形ABCD是平行四边形.求证：AB=CD，BC=DA.证明：连接AC.∵四边形ABCD是平行四边形，∴AB∥CD， BC∥DA（平行四边形的定义）.∴∠1=∠2，∠3=∠4.∵AC=CA，∴△ABC≌△CDA.∴AB=CD，BC=DA.证明：∵四边形ABCD是平行四边形，∴AB∥CD， BC∥DA（平行四边形的定义）.∴∠A+∠B =180°，∠B+∠C =180°.∴∠A =∠C.同理可得： ∠B =∠D.试一试请你证明：平行四边形的对角相等. 定理 平行四边形的对边相等. 定理 平行四边形的对角相等.归纳小结例1 已知：如图，在 ABCD中，E，F是对角线AC上的两点，并且AE=CF.求证：BE=DF.证明：∵四边形ABCD是平行四边形，∴AB=CD（平行四边形的对边相等） AB∥CD（平行四边形的定义）.∴∠BAE=∠DCF.又∵AE=CF，∴△ABE≌△CDF.∴BE=DF.练习已知平行四边形一个内角的度数，能确定其他内角的度数吗？说说你的理由.如图，四边形ABCD是平行四边形，求： （1）∠ADC和∠BCD的度数； （2）AB和BC的长度.随堂练习12cm280°100°80°100°3.平行四边形的一条角平分线分对边为3和4两部分，求平行四边形的周长.解：如图，∵ ABCD中，AD∥BC，∴∠1=∠3，又∠1=∠2，∴∠2=∠3，∴AB=BE.当BE=3时，AB=BE=3，∴ ABCD的周长为：（AB+BC）×2=（3+7）×2=20.当BE=4时，AB=BE=4，∴ ABCD的周长为：（AB+BC）×2=（4+7）×2=22.课堂小结 定义：两组对边分别平行的四边形叫做平行四边形.1.完成课本P137 习题6.1，2.完成练习册本课时的习题.课后作业谢谢欣赏