初中数学北师大版九年级下册1 二次函数试讲课ppt课件

这是一份初中数学北师大版九年级下册1 二次函数试讲课ppt课件，共22页。PPT课件主要包含了复习导入，探究新知，yx2，①列表，②描点，③连线，抛物线，y2x2，与抛物线，有什么关系等内容，欢迎下载使用。

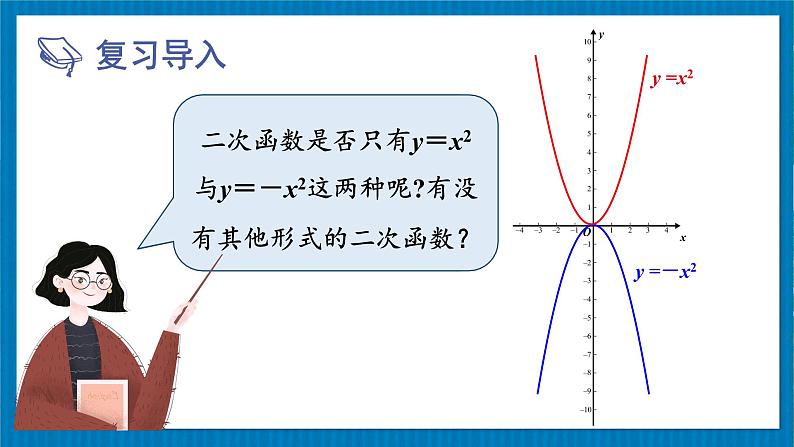
二次函数y＝x2与y=－x2的图象一样吗？它们有什么相同点？不同点？
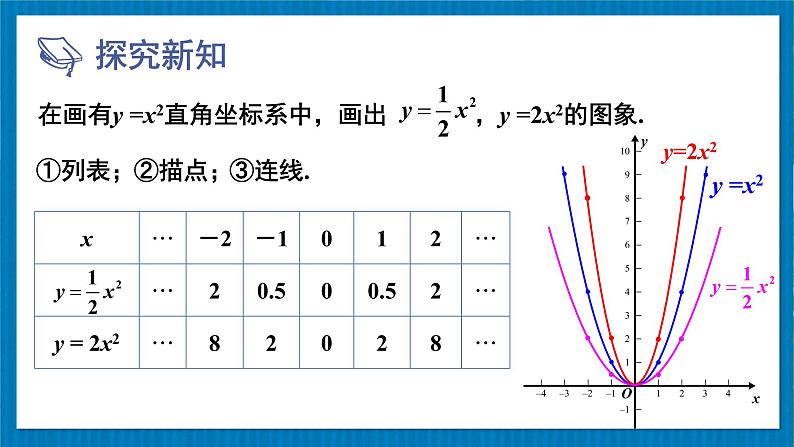
二次函数是否只有y＝x2与y＝－x2这两种呢?有没有其他形式的二次函数？
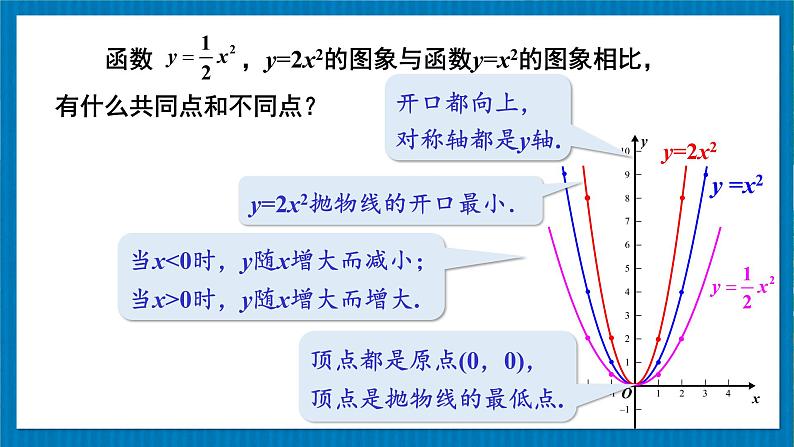
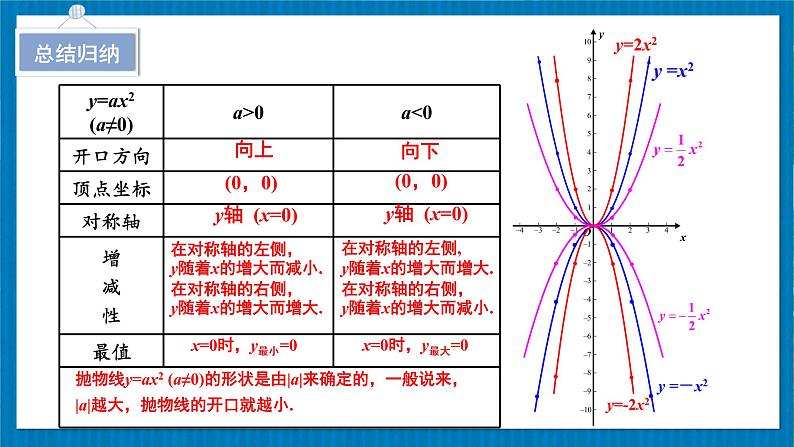
开口都向上，对称轴都是y轴.
顶点都是原点(0，0)，顶点是抛物线的最低点.
当x<0时，y随x增大而减小；当x>0时，y随x增大而增大.
y=2x2抛物线的开口最小．
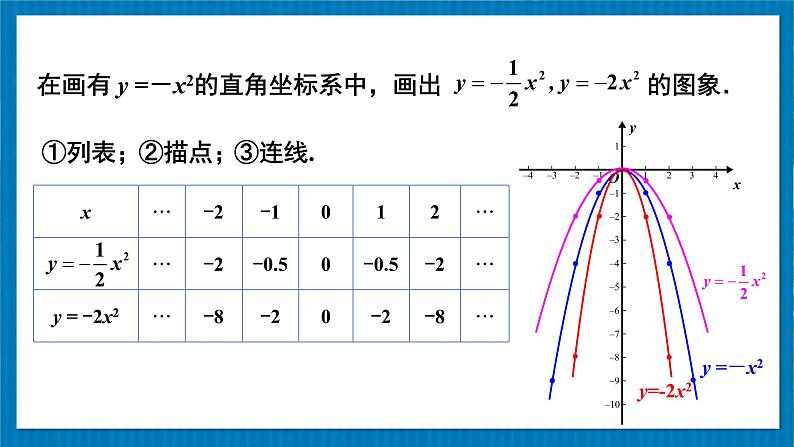
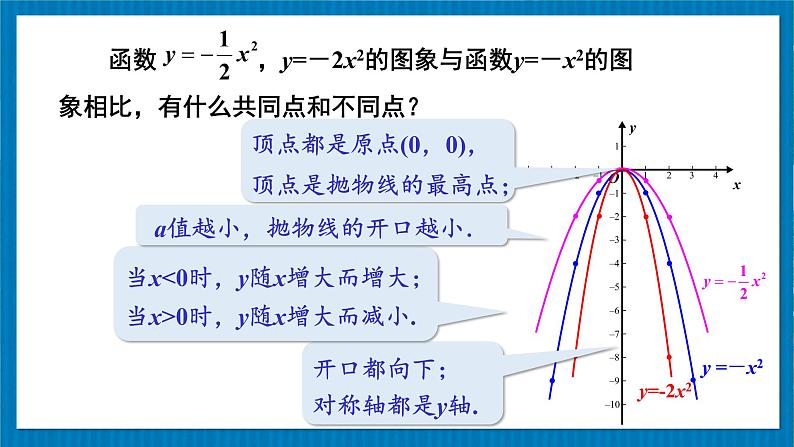
函数 ，y=－2x2的图象与函数y=－x2的图象相比，有什么共同点和不同点？
开口都向下；对称轴都是y轴.
顶点都是原点(0，0)，顶点是抛物线的最高点；
当x<0时，y随x增大而增大；当x>0时，y随x增大而减小.
a值越小，抛物线的开口越小．
在对称轴的左侧，y随着x的增大而减小.在对称轴的右侧，y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.在对称轴的右侧，y随着x的增大而减小.
抛物线y=ax2 (a≠0)的形状是由|a|来确定的，一般说来，|a|越大，抛物线的开口就越小.
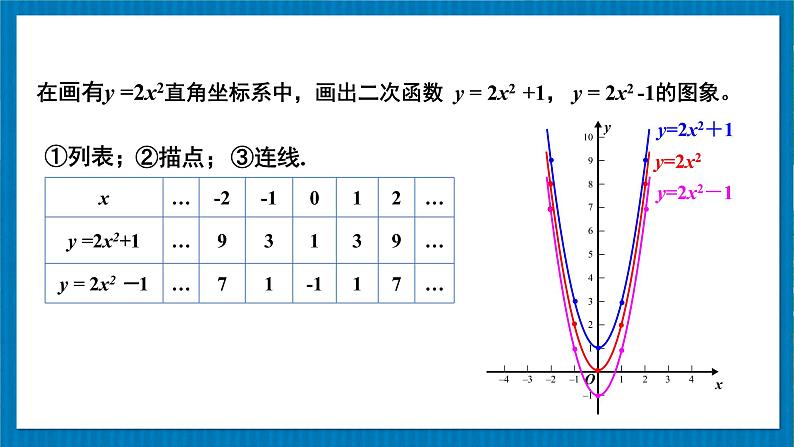
在画有y =2x2直角坐标系中，画出二次函数 y = 2x2 +1， y = 2x2 -1的图象。
二次函数y=2x2，y=2x2+1，y=2x2-1的图象都是抛物线，并且形状相同，只是位置不同.
将二次函数y=2x2的图象向上平移1个单位，就得到函数y=2x2+1的图象.
将二次函数y=2x2的图象向下平移1个单位，就得到函数y=2x2－1的图象.
将二次函数y=2x2＋1的图象向____平移____个单位，就得到函数y=2x2－1的图象.
y = 2x2+1 ， y = 2x2 -1
y = ax2+c（c＞0）
y = ax2＋c（c＜0）
二次函数y = ax2 +c的图象和性质:
x=0时，y最小值=c
x=0时，y最大值=c
1. 抛物线y＝2x2＋3可以由抛物线y＝2x2向 平移 个单位得到．2. 抛物线y＝－ x2+1向 平移 个单位后，会得到抛物线y=－ x2．3. 抛物线y＝－2x2－5的开口方向 ，对称轴是 ，顶点坐标是 .
4. 下列各组抛物线中能够互相平移彼此得到对方的是( ) A. y＝2x2与y＝3x2 B.y= x2+2与y=2x2+ C. y＝2x2与y＝x2+2 D.y＝x2与y＝x2－2
5. 对于二次函数y＝－ x2+2，当x为xl和x2时，对应的函数值分别为y1和y2，若x1>x2>0，则y1与y2的大小关系是( ) A.y1>y2 B.y1当x＞0时，y随x增大而减小.
6. 写出下列各组函数图象的开口方向、对称轴和顶点.（1）y= x2+3; （2）y=-3x2-4.
解：（1）开口向上，对称轴为y轴，顶点为（0，3）. （2）开口向下，对称轴为y轴，顶点为（0，-4）.
7. 求抛物线y=2x2－1关于x轴对称的抛物线的解析式.
解：抛物线y=2x2－1关于x轴对称的抛物线的解析式为y=－2x2+1.
8. 二次函数y＝3x2－ 的图象与二次函数y=3x2的图象有什么关系？它是轴对称图形吗？它的开口方向、对称轴和顶点坐标分别是什么？画图看一看.
9. 二次函数 的图象与二次函数 的图象有什么关系？