北师版数学七年级下册 4.3.2利用“角边角”“角角边”判定三角形全等 课件

这是一份北师版数学七年级下册 4.3.2利用“角边角”“角角边”判定三角形全等 课件，共20页。

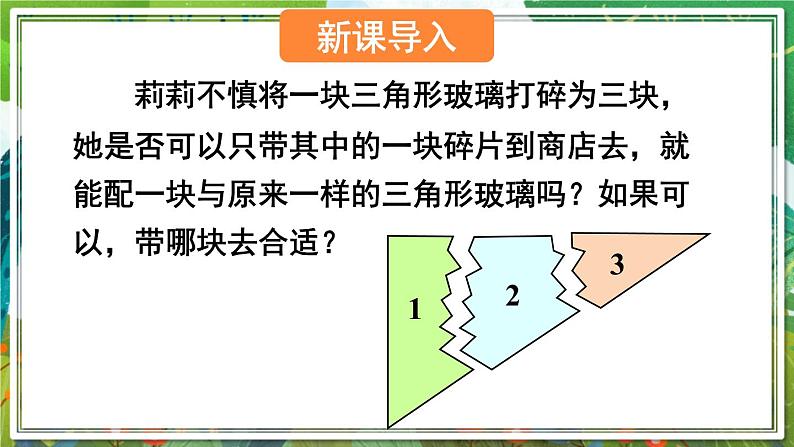
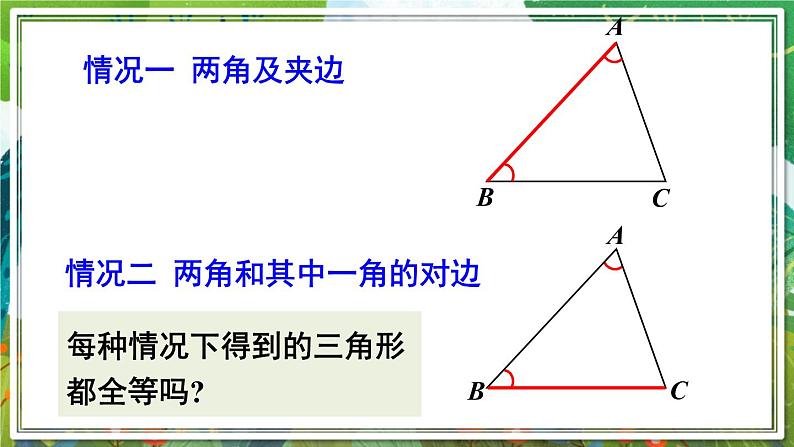
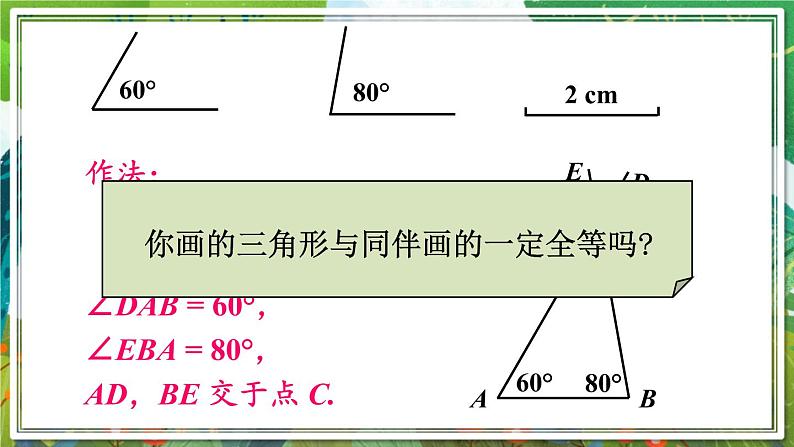
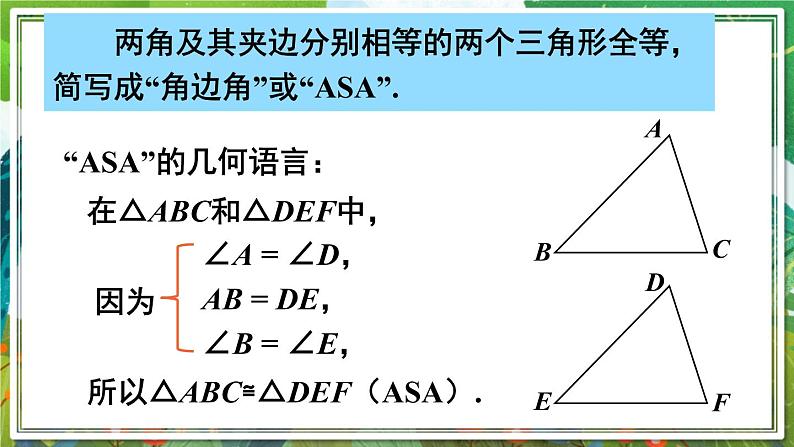
莉莉不慎将一块三角形玻璃打碎为三块，她是否可以只带其中的一块碎片到商店去，就能配一块与原来一样的三角形玻璃吗？如果可以，带哪块去合适？ 我们知道：如果给出一个三角形三条边的长度，那么因此得到的三角形都是全等. 如果已知一个三角形的两角及一边，那么有几种可能的情况呢?每种情况下得到的三角形都全等吗?情况一 两角及夹边情况二 两角和其中一角的对边 如果“两角及一边”条件中的边是两角所夹的边，比如三角形的两个内角分别是60°和80°，它们所夹的边为 2 cm，你能画出这个三角形吗？60°80°2 cm60°80°2 cm作法：（1）画 AB = 2 cm；（2）在 AB 的同旁画∠DAB = 60°，∠EBA = 80°，AD，BE 交于点 C.ABDEC60°80° 两角及其夹边分别相等的两个三角形全等，简写成“角边角”或“ASA”.“ASA”的几何语言：在△ABC和△DEF中，因为∠A = ∠D，AB = DE，∠B = ∠E，所以△ABC≌△DEF（ASA）.注意：书写两个三角形全等的条件“ASA”时，一定要把夹边相等写在中间，以突出角边角的位置以及对应关系. 如果“两角及一边”条件中的边是其中一角的对边，情况会怎样呢？ 若三角形的两个内角分别是60°和70°，且70°所对的边为 3cm，你能画出这个三角形吗?60°70°3 cm60°70°3 cmAB根据三角形的内角和为180°，所以第三个角度数为180°- 60°- 70°= 50°.D60°E50°C70° 两角分别相等且其中一组等角的对边相等的两个三角形全等，简写成“角角边”或“AAS”. 如图所示，AB 与 CD 相交于点 O，O 是 AB 的中点，∠A = ∠B，△AOC 与△BOD 全等吗？为什么？解：全等.理由如下：在△AOC 和△BOD 中，∠A = ∠BAO = BO（O是 AB 中点）∠AOC = ∠BOD（对顶角相等）所以△AOC≌△BOD（ASA）因为 1. 如图，已知∠A =∠D，∠1 = ∠2，那么要得到△ABC ≌ △DEF，还应给出的条件是（ ） A.∠E =∠B B.ED = BC C.AB = EF D.AF = CDD 2. 如图，已知∠A =∠D，AB = CD，可得△ABO≌_______，理由是______.△DCOAAS 3. 如图，点 A，B，C，D 在同一条直线上，BE//DF，∠A=∠F，AB=FD. 试说明：AE=FC.解：因为BE // DF，所以∠ABE = ∠D，在△ABE 和 △FDC 中，∠ABE = ∠D，AB = FD，∠A = ∠F，所以△ABE ≌ △FDC（ASA）所以AE = FC . 4. 如图，AB=AE，∠1=∠2，∠C=∠D.试说明：△ABC ≌ △AED.解：理由如下：因为∠1=∠2，所以∠1+∠EAC =∠2+∠EAC，即∠BAC = ∠EAD，在△ABC 和 △AED 中，∠C = ∠D,∠BAC = ∠EAD,AB = AE,所以△ABC ≌ △AED （AAS）. 两角及其夹边分别相等的两个三角形全等，简写成“角边角”或“ASA”. 两角分别相等且其中一组等角的对边相等的两个三角形全等，简写成“角角边”或“AAS”.1.从教材习题中选取；2.完成练习册本课时的习题.谢谢欣赏