数学七年级下册7.5 多边形的内角和与外角和多媒体教学ppt课件

这是一份数学七年级下册7.5 多边形的内角和与外角和多媒体教学ppt课件，共18页。PPT课件主要包含了找一找，认一认，类比思想，记一记，内角角，辩一辩，探究活动，特殊到一般的方法，化归思想，具体到抽象等内容，欢迎下载使用。
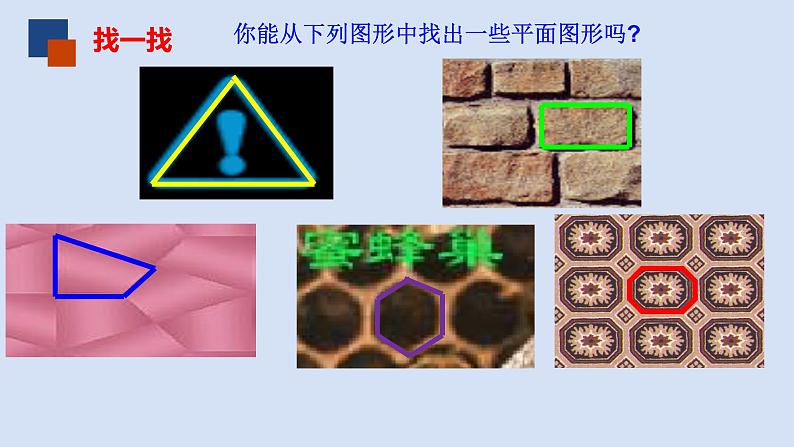
你能从下列图形中找出一些平面图形吗?
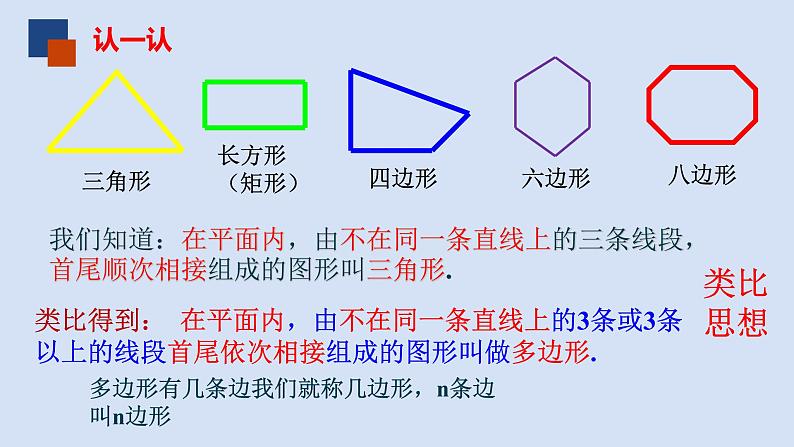
我们知道：在平面内，由不在同一条直线上的三条线段，首尾顺次相接组成的图形叫三角形.
类比得到： 在平面内，由不在同一条直线上的3条或3条以上的线段首尾依次相接组成的图形叫做多边形.
多边形有几条边我们就称几边形，n条边叫n边形
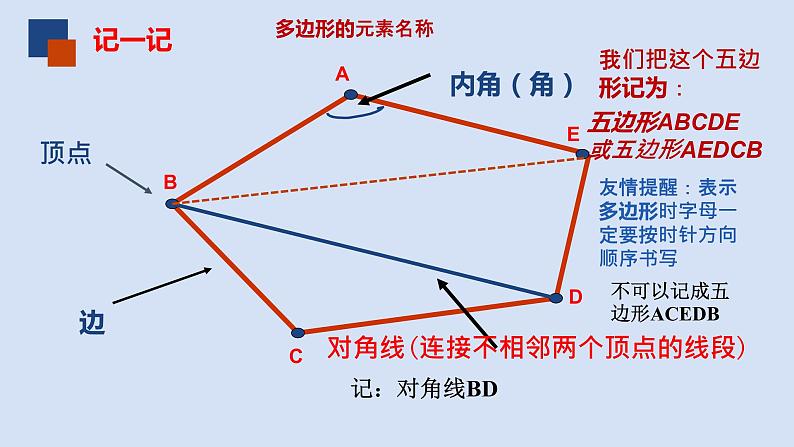
对角线(连接不相邻两个顶点的线段)
我们把这个五边形记为：
五边形ABCDE或五边形AEDCB
友情提醒：表示多边形时字母一定要按时针方向顺序书写
不可以记成五边形ACEDB
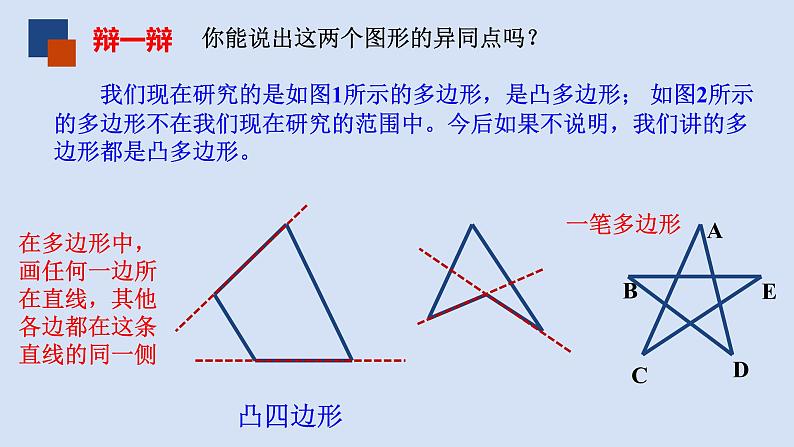
我们现在研究的是如图1所示的多边形，是凸多边形； 如图2所示的多边形不在我们现在研究的范围中。今后如果不说明，我们讲的多边形都是凸多边形。
你能说出这两个图形的异同点吗？
在多边形中，画任何一边所在直线，其他各边都在这条直线的同一侧
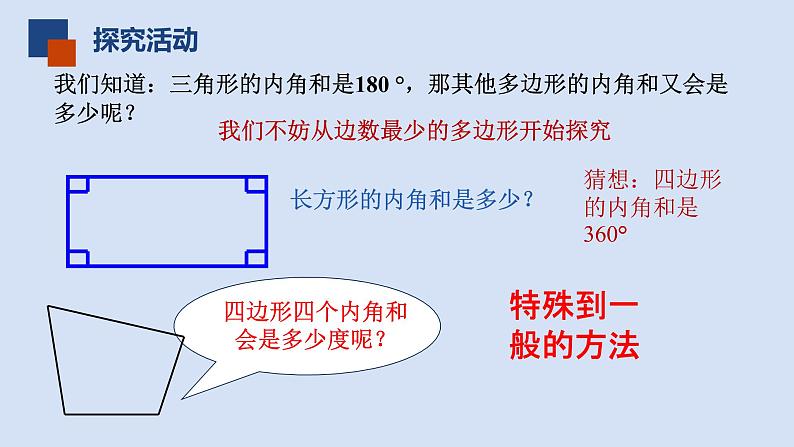
长方形的内角和是多少？
我们知道：三角形的内角和是180 °，那其他多边形的内角和又会是多少呢？
我们不妨从边数最少的多边形开始探究
猜想：四边形的内角和是360°
360°=180 ° ×2
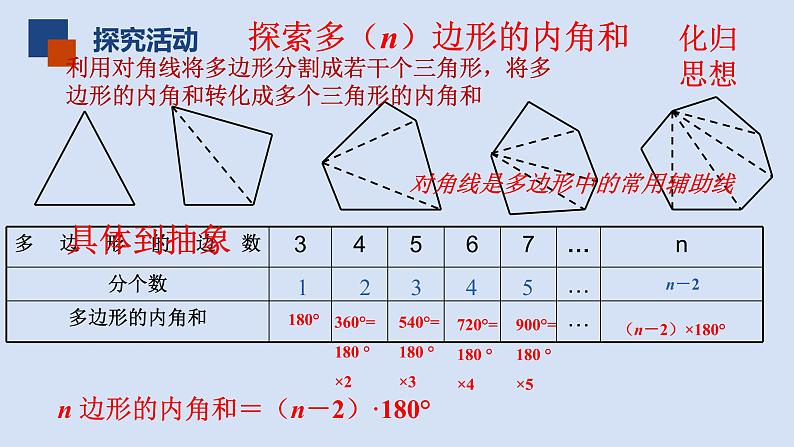
（n－2）×180°
n 边形的内角和＝（n－2）·180°
540°=180 ° ×3
720°=180 ° ×4
900°=180 ° ×5
探索多（n）边形的内角和
利用对角线将多边形分割成若干个三角形，将多边形的内角和转化成多个三角形的内角和
对角线是多边形中的常用辅助线
此分割方式，将多边形分成（n-1）个三角形，故所有三角形的内角和为（n-1）×180 °，边上一点周围所形成的平角不是多边形的内角，因此n边形的内角和为 （n-1）×180 °- 180 °= (n-2)×180 °
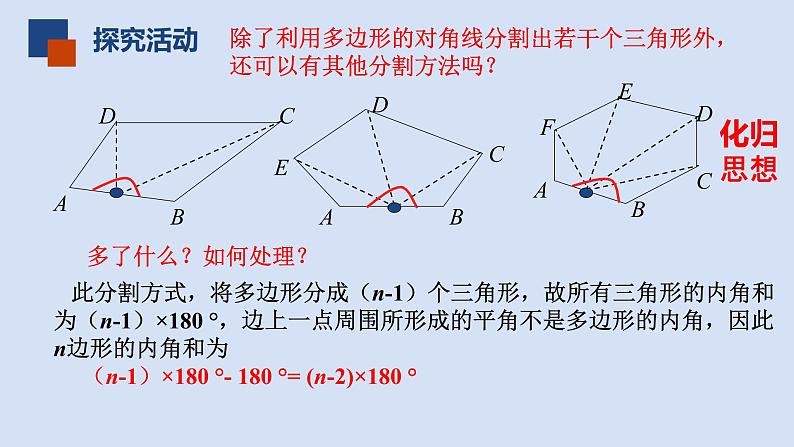
除了利用多边形的对角线分割出若干个三角形外，还可以有其他分割方法吗？
此分割方式，将n边形分割出n个三角形，故所有三角形内角和为n·180 °，但每个图中都有一个以红圈圈住的点处的圆周角360 °不是这个多边形的内角，因此n边形的内角和为 n ·180 °- 360 °= (n-2) ·180 °
除了上面的两种分割方法分割出多个三角形外，还有吗？
n 边形的内角和是180度的倍数，即多边形的内角和能被180整除。
n 边形的内角和的得出是借助分割化归成多个三角形的内角和计算而成
1.七边形内角和为 .
2.十边形内角和为 .
3.多边形内角和为1080°，则它是 边形.
900 °=（7-2） ×180 °
1440 °=（10-2） ×180 °
八（n-2）=1080 ° n=8
例1 如图，在四边形ABCD中，∠A与∠C互补，∠ABC、∠ADC的平分线分别交CD、AB于点E、F ，∠1与∠2有怎样的数量关系？为什么？
理由：在四边形ABCD中，∠A+∠ABC+∠C+∠ADC = （4-2） ×180 °=360°∵ ∠A+∠C = 180 °∴ ∠ABC+∠ADC = 360°-（∠A+∠C ）=180 °又∵ BE、DF分别平分∠ABC、∠ADC ，得∴ ∠2=0.5∠ABC，∠1= 0.5∠ADC ∴ ∠1+∠2=0.5(∠ADC +∠ABC)=0.5×180 °=90 °即∠1与∠2互余.
【思维点拨】求角的度数时，常考虑将其放置到多边形内来求值.
例2 如图,有一个五角星，你会求∠A+ ∠B+ ∠C+ ∠D+ ∠E的值吗？
提示：连结CD即可求得。
解：设BD、CE交于点O， 在△BOE、 △COD中∠B+ ∠E+∠BOE=∠ECD+ ∠BDC+∠COD=180 °又∠BOE=∠COD∴∠B+ ∠E=∠ECD+ ∠BDC 在△ACD中，∠A+ ∠ACD+ ∠ADC=180 ° ∴ ∠A+ ∠B+ ∠ACE+ ∠ADB+ ∠E=180 °
多边形截角后的边数问题
典例1 有一六边形，截去一个三角形，内角和会发生怎样变化？请画图说明。
典例2 若一个多边形除了一个内角外，其余各内角之和为2570°，则这个内角的度数为(   )A．90° B．105°C．130° D．120°
【答案】C【提示】本题主要考查了多边形的外角和内角. 先用2570°÷180°，看余数是多少，再把余数补成180°【详解】解：∵2570°÷180°=14…50°，又130°+50°=180°∴这个内角度数为130°故选C
1.已知四边形4个内角的度数比是1︰2︰3︰4,那么这个四边形中最大角的度数是 .2.一个五边形中有三个内角是直角，其余两个内角都是n°，则n= .3.六角螺母的面是六边形，它的内角都相等，则这个六边形的每个内角是 .4. 如图，在三角形纸片ABC中剪去∠C得到四边形ABDE，且∠1+∠2=230°．求纸片中∠C的度数.
变式：已知∠C的度数，同学们可以求哪两个角的和.
2n+3×90°=(5-2) ×180°=540° n=135°
(6-2) ×180° ÷ 6=120°
4、解：在四边形ABDE中，∠1+∠2+∠A+∠B=360°,∠1+∠2=230°,得 ∠A+∠B=360°-230 ° =130 °， 在△ABC中，∠A+∠B+∠C=180°，得 ∠C=180°-（∠A+∠B）=50°.
说明：我们用多边形的内角和解决了昨天的思考题，先回忆昨天的方法，再比较两种方法的简易程度.我们再继续学习还会有新的方法解决本题。