数学七年级下册第9章 整式乘法与因式分解9.5 多项式的因式分解背景图课件ppt

这是一份数学七年级下册第9章 整式乘法与因式分解9.5 多项式的因式分解背景图课件ppt，共22页。PPT课件主要包含了情境创设，因式分解及相关概念，ab2，寻找公因式的步骤，abc，找一找，ma+mb+mc，-2m•-4m，-2m•6，随堂练习等内容，欢迎下载使用。
一块场地由三个矩形组成，这些矩形的长分别为2.8m，4.9m，2.3m，宽都是37m，求这块场地的面积．
2.8×37+4.9×37+2.3×37
（2.8+4.9+2.3）×37
根据乘法分配律ab＋ac＋ad＝a（b＋c＋d）
换一种看法，就是把单项式乘多项式的法则a（b＋c＋d）＝ab＋ac＋ad反过来，就得到ab＋ac＋ad＝a（b＋c＋d）．
a 是多项式ab＋ac＋ad各项都含有的因式．
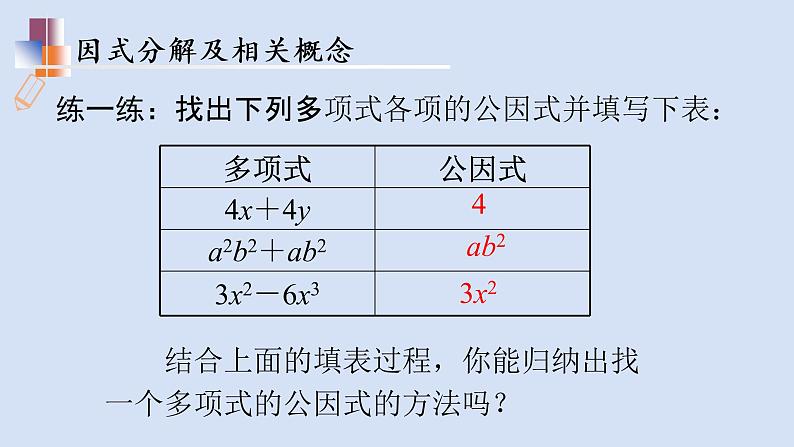
　　结合上面的填表过程，你能归纳出找一个多项式的公因式的方法吗？
1.看系数：当多项式的各项系数多是整数时，公因式的系数应取各项系数的最大公约数．
2.看字母：公因式的字母应取多项式中各项都含有的相同字母．
3.看指数：相同字母的指数取次数最低的．
定系数：各项系数的最大公约数。
定字母：多项式中各项相同的字母。
定指数：相同字母的最低次数。
请指出下列多项式各项的公因式：
x2-1 (x+1)(x-1)
x2-1 = (x+1)(x-1)
等式的特征：左边是多项式，右边是几个整式的乘积
不是，等号右边不是几个整式的积的形式.
不是，等左边不是多项式.
如果一个多项式的各项含有公因式，那么就可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式，这种分解因式的方法叫做提公因式法.
( a+b+c )
例1：把下列各式分解因式.
(1) 5x3－10x2
解:原式 =5x2•x－5x2•2
=5x2(x－2)
(2) 12ab2c－6ab
解:原式 =6ab•2bc－6ab•1
=6ab(2bc－1)
注意：1.如果提出的公因式与多项式中的某一项相同,那么提取后多项式中的这一项剩下“1”结果中的“1”不能漏写；
2.多项式有几项，提出公因式后另一项也有几项.
把-2m3+8m2-12m分解因式
解：原式 =-2m•m2
分析：当多项式的第一项系数为负数时,通常把“－”作为公因式的负号写在括号外,使括号内第一项的系数为“＋”.
=-2m(m2－4m+6)
注意点：①若首项系数为负时，一般要提出“－”号； ②不能漏项； ③是否分解到最后结果。
1.下列各式中从左到右的变形属于分解因式的是（　　）A. a(a+b-1)=a2+ab-a B. a2-a-2=a(a-1)-2C. -4a2+9b2=(-2a+3b)(2a+3b) D.2x +1=x(2+ )
2.把x2+3x+c分解因式得x2+3x+c=(x+1)·(x+2)，则c的值为（ ）A.2 B.3 C.-2 D.-3
3.已知x2-2x-3=0，则2x2-4x的值为（ ）A.-6B.6 C.-2或6D.-2或30
4.若(x+y)3-xy(x+y)=(x+y)·A，则A为（ ）A.x2+y2B.x2-xy+y2 C.x2-3xy+y2D.x2+xy+y2
5.下列多项式中，能用提公因式法因式分解的是（ ）A.x2-y2B.x2+2x C.x2+y2D.x2-xy+y2
6.用提公因式法因式分解：（1）6p(p+q)-4q(p+q) （2）2a(x-y)-3b(y-x)；（3）28x4-21x3+7xy；（4）-10m4n2+8m4n-2m3n.
解： （1）原式=2(p+q)(3p-2q).
（2）原式=2a(x-y)+3b(x-y) =(x-y)(2a+3b).
（3）原式=7x(4x3-3x2-y).
（4）原式= -m3n(10mn-8m+2)
7.先因式分解，再计算求值：4a(x+7)-3(x+7)，其中a=-5，x=3.
解：原式=(x+7)(4a-3) ∵a=-5，x=3，∴原式=(3+7) ×[4×(-5)-3]=10×(-23)=-230.