2022-2023学年八年级数学上学期期末考试满分全攻略（苏科版）【常考60题考点专练】

这是一份2022-2023学年八年级数学上学期期末考试满分全攻略（苏科版）【常考60题考点专练】，文件包含江苏八年级上学期期末常考60题考点专练解析版docx、江苏八年级上学期期末常考60题考点专练原卷版docx等2份试卷配套教学资源，其中试卷共49页， 欢迎下载使用。
A．4的平方根是±2B．8的立方根是±2
C．D．
2．（2021秋•惠山区校级期末）在，﹣，π，0，，0.6，0.1212212221…（相邻两个1之间2的个数逐次加1）这些数中，无理数的个数是（ ）个．
A．1B．2C．3D．4
3．（2021秋•沭阳县校级期末）在平面直角坐标系中，点（8，﹣15）所在的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
4．（2021秋•海陵区校级期末）已知直线y＝kx+b经过第一、二、四象限，那么直线y＝bx+k一定不经过（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
5．（2021秋•新吴区期末）等腰三角形的两边长分别为4和9，这个三角形的周长是（ ）
A．17B．22C．17或22D．17和22
6．（2021秋•玄武区校级期末）下面四个图形中，其中不一定是轴对称图形的是（ ）
A．等腰三角形B．正方形C．等边三角形D．直角三角形
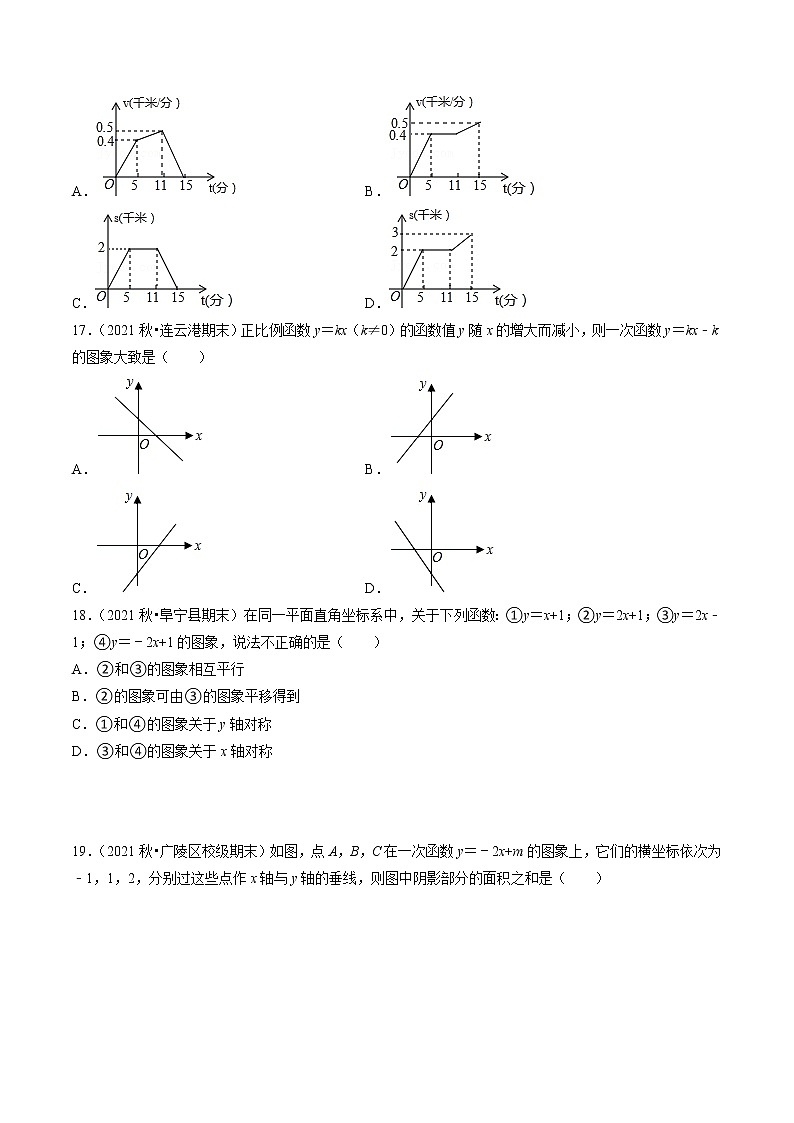
7．（2021秋•沭阳县校级期末）下列图形中，是轴对称图形的是（ ）
A．B．
C．D．
8．（2021秋•泗洪县期末）在平面直角坐标系中，点P（2，﹣3）关于x轴对称的点的坐标是（ ）
A．（2，3）B．（2，﹣3）C．（﹣2，3）D．（﹣2，﹣3）
9．（2021秋•滨海县期末）已知实数x，y满足+（y+1）2＝0，则x﹣y等于（ ）
A．1B．﹣1C．﹣3D．3
10．（2021秋•大丰区期末）若点P在第二象限，且点P到x轴的距离为2，到y轴的距离为1，则点P的坐标为（ ）
A．（1，﹣2）B．（2，1）C．（﹣1，2）D．（2，﹣1）
11．（2021秋•盱眙县期末）已知点（﹣2，y1），（﹣1，y2），（1，y3）都在直线y＝﹣3x上，则y1，y2，y3的大小关系是（ ）
A．y1＞y2＞y3B．y1＜y2＜y3C．y3＞y1＞y2D．y3＜y1＜y2
12．（2021秋•亭湖区期末）如图，△AOC≌△BOD，点A与点B是对应点，那么下列结论中错误的是（ ）
A．AB＝CDB．AC＝BDC．AO＝BOD．∠A＝∠B
13．（2021秋•鼓楼区校级期末）10的算术平方根是（ ）
A．10B．C．﹣D．±
14．（2021秋•沭阳县校级期末）下列图象中，表示y是x的函数的是（ ）
A．B．
C．D．
15．（2021秋•无锡期末）某商场为了增加销售额，推出“七月销售大酬宾”活动，其活动内容为：“凡七月份在该商场一次性购物超过100元以上者，超过100元的部分按9折优惠．”在大酬宾活动中，小王到该商场为单位购买单价为60元的办公用品x件（x＞2），则应付货款y（元）与商品件数x的函数关系式是（ ）
A．y＝54x（x＞2）B．y＝54x+10（x＞2）
C．y＝54x+90（x＞2）D．y＝54x+100（x＞2）
16．（2021秋•梁溪区校级期末）小刚以400米/分的速度匀速骑车5分，在原地休息了6分，然后以500米/分的速度骑回出发地，设小刚离家路程为s（千米），速度为v（千米/分），时间为t（分）．下列函数图象能表达这一过程的是（ ）
A．B．
C．D．
17．（2021秋•连云港期末）正比例函数y＝kx（k≠0）的函数值y随x的增大而减小，则一次函数y＝kx﹣k的图象大致是（ ）
A．B．
C．D．
18．（2021秋•阜宁县期末）在同一平面直角坐标系中，关于下列函数：①y＝x+1；②y＝2x+1；③y＝2x﹣1；④y＝﹣2x+1的图象，说法不正确的是（ ）
A．②和③的图象相互平行
B．②的图象可由③的图象平移得到
C．①和④的图象关于y轴对称
D．③和④的图象关于x轴对称
19．（2021秋•广陵区校级期末）如图，点A，B，C在一次函数y＝﹣2x+m的图象上，它们的横坐标依次为﹣1，1，2，分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积之和是（ ）
A．1B．3C．3（m﹣1）D．
20．（2021秋•玄武区校级期末）如图，红红书上的三角形被墨迹污染了一部分，她根据所学的知识很快就画了一个与书上完全一样的三角形，那么红红画图的依据是（ ）
A．SSSB．SASC．ASAD．AAS
21．（2021秋•滨海县期末）∠AOB的平分线上一点P到OA的距离为4，Q是OB上任一点，则（ ）
A．PQ≥4B．PQ＞4C．PQ≤4D．PQ＜4
22．（2021秋•射阳县校级期末）若等腰三角形中有一个角为50度，则这个等腰三角形的顶角的度数为（ ）
A．50°B．80°C．65°或50°D．50°或80°
23．（2021秋•滨湖区期末）如图，已知直线y＝ax+2与直线y＝mx+b的交点的横坐标是﹣2．根据图象有下列四个结论：①a＞0；②b＜0；③方程ax+2＝mx+b的解是x＝﹣2；④不等式ax﹣b＞mx﹣2的解集是x＞﹣2．其中正确的结论个数是（ ）
A．1B．2C．3D．4
24．（2021秋•滨湖区期末）满足下列条件的△ABC不是直角三角形的是（ ）
A．∠A：∠B：∠C＝3：4：5B．BC＝1，AC＝2，AB＝
C．BC：AC：AB＝3：4：5D．BC＝1，AC＝2，AB＝
二．填空题（共19小题）
25．（2018秋•邗江区校级期末）已知函数y＝（m﹣1）+1是一次函数，则m＝ ．
26．（2021秋•滨海县期末）已知y关于x的函数y＝﹣x+2+m是正比例函数，则m＝ ．
27．（2021秋•镇江期末）一次函数y＝ax+b在直角坐标系中的图象如图所示，则化简﹣|a+b|的结果是 ．
28．（2021秋•广陵区校级期末）已知点（﹣2，y1），（2，y2）都在直线y＝2x﹣3上，则y1 y2．（填“＜”或“＞”或“＝”）
29．（2021秋•丹阳市期末）一次函数y＝kx﹣3的图象经过点（﹣1，3），则k＝ ．
30．（2021秋•滨海县期末）已知一次函数y＝kx+b的图象与x轴的交点坐标是（﹣1，0），则关于x的一元一次方程kx+b＝0的解是 ．
31．（2021秋•大丰区期末）如图，直线y＝kx+b与直线y＝mx+n交于P（1，），则方程组的解是 ．
32．（2021秋•镇江期末）如图，△ABC≌△DFE，∠B＝80°，∠ACB＝30°，则∠D＝ ．
33．（2021秋•海陵区校级期末）结合图，用符号语言表达定理“斜边和一条直角边分别相等的两个直角三角形全等”的推理形式：
在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，
AC＝DF

∴Rt△ABC≌Rt△DEF．
34．（2021秋•仪征市期末）如图所示，△ABC中，∠C＝90°，AD平分∠BAC，AB＝6，CD＝2，则△ABD的面积是 ．
35．（2021秋•鼓楼区校级期末）如图，在△ABC中，∠C＝90°，AB的垂直平分线交AB、AC于点D、E，若AC＝8，BD＝5，则△ADE的面积是 ．
36．（2021秋•溧水区期末）已知：如图，AB＝AC＝12cm，AB的垂直平分线分别交AC、AB于D、E，△ABD的周长等于28cm，则DC的长为 ．
37．（2021秋•广陵区期末）如图，在△ABC中，AB＝AC．以点C为圆心，以CB长为半径作圆弧，交AC的延长线于点D，连接BD．若∠A＝32°，则∠CDB的大小为 度．
38．（2021秋•仪征市期末）在△ABC中，∠A＝40°，当∠B＝ 时，△ABC是等腰三角形．
39．（2021秋•射阳县校级期末）如图，已知边长为2的正三角形ABC，两顶点A，B分别在平面直角坐标系的x轴、y轴的正半轴上滑动，点C在第一象限，连接OC，则OC长的最大值是 ．
40．（2021秋•新吴区期末）直角三角形两边的长为6和8，则该直角三角形斜边上的中线长为 ．
41．（2021秋•溧水区期末）直角三角形两直角边长分别为5cm和12cm，则斜边上的中线长为 cm．
42．（2021秋•阜宁县期末）如图，已知∠B＝45°，AB＝2cm，点P为∠ABC的边BC上一动点，则当BP＝ cm时，△BAP为直角三角形．
43．（2021秋•邗江区期末）如图，在△ABC中，点D、E分别为边BC、AC上的点，连接DE，将△CDE沿DE翻折得到△C′DE，使C′D∥AB．若∠A＝75°，∠C＝45°，则∠C′EA的大小为 °．
三．解答题（共17小题）
44．（2021秋•盱眙县期末）如图，函数y＝2x和y＝ax+4的图象相交于点A（m，3）
（1）求m，a的值；
（2）根据图象，直接写出不等式2x＞ax+4的解集．
45．（2021秋•惠山区校级期末）抗击疫情，我们在行动．某药店销售A型和B型两种型号的口罩，销售一箱A型口罩可获利120元，销售一箱B型口罩可获利140元．该药店计划一次购进两种型号的口罩共100箱，其中B型口罩的进货量不超过A型口罩的3倍．设购进A型口罩x箱，这100箱口罩的销售总利润为y元．
（1）求y与x的函数关系式；
（2）该商店购进A型、B型口罩各多少箱，才能使销售利润最大？最大利润是多少？
（3）若限定该药店最多购进A型口罩70箱，则这100箱口罩的销售总利润能否为12500元？请说明理由．
46．（2021秋•南京期末）如图，在△ABC中，AB＝AC，AD⊥BC于点D．
（1）若∠C＝42°，求∠BAD的度数；
（2）若点E在边AB上，EF∥AC交AD的延长线于点F．求证：AE＝FE．
47．（2021秋•无锡期末）（1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；
（2）直接写出A′，B′，C′三点的坐标：A′（ ， ），B′（ ， ），C′（ ， ）．
48．（2021秋•邗江区期末）如图，∠ACB＝∠ADB＝90°，M、N分别是AB、CD的中点．
（1）求证：MN⊥CD；
（2）若AB＝50，CD＝48，求MN的长．
49．（2021秋•盱眙县期末）如图，一高层住宅发生火灾，消防车立即赶到距大厦9米处（车尾到大厦墙面），升起云梯到火灾窗口，已知云梯长15米，云梯底部距地面3米，问：发生火灾的住户窗口距离地面BD有多高？
50．（2021秋•射阳县校级期末）阅读下列一段文字，然后回答下列问题：
已知平面内两点M（x1，y1）、N（x2，y2），则这两点间的距离可用下列公式计算：MN＝．
例如：已知P（3，1）、Q（1，﹣2），则这两点的距离PQ＝＝．
特别地，如果两点M（x1，y1）、N（x2，y2）所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴，那么这两点间的距离公式可简化为MN＝|x1﹣x2|或|y1﹣y2|．
（1）已知A（1，2）、B（﹣2，﹣3），试求A、B两点间的距离；
（2）已知A、B在平行于y轴的同一条直线上，点A的纵坐标为5，点B的纵坐标为﹣1，试求A、B两点间的距离；
（3）已知△ABC的顶点坐标分别为A（0，4）、B（﹣1，2）、C（4，2），你能判定△ABC的形状吗？请说明理由．
51．（2021秋•滨海县期末）甲、乙两家草莓采摘园的草莓品质相同，销售价格也相同．“五一”假期，两家均推出了优惠方案，甲采摘园的优惠方案：游客进园需购买60元的门票，采摘的草莓六折优惠；乙采摘园的优惠方案：游客进园不需购买门票，采摘的草莓超过一定数量后，超过部分打折优惠．优惠期间，设某游客的草莓采摘量为x（千克），在甲采摘园所需总费用为y甲（元），在乙采摘园所需总费用为y乙（元），图中折线O﹣A﹣B表示y乙与x之间的函数关系．
（1）求y甲、y乙与x之间的函数关系式；
（2）当游客采摘15千克的草莓时，你认为他在哪家草莓园采摘更划算？
52．（2021秋•滨海县期末）如图，已知AB∥CF，D是AB上一点，DF交AC于点E，若AB＝BD+CF，求证：△ADE≌△CFE．
53．（2021秋•溧水区期末）如图，点B、E、C、F在同一直线上，AB＝DE，AC＝DF，BE＝CF，求证：△ABC≌△DEF．
54．（2021秋•梁溪区期末）如图，△ABC中，AB＝AC，点D，E在边BC上，且BD＝CE．
（1）求证：△ABD≌△ACE；
（2）若∠B＝40°，AB＝BE，求∠DAE的度数．
55．（2021秋•江都区期末）如图，在△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC交AC于点D，点E是AB的中点，连接DE．
（1）求证：△ABD是等腰三角形；
（2）求∠BDE的度数．
56．（2021秋•江阴市期末）明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地°送行二步恰竿齐，五尺板高离地…”翻译成现代文为：如图，秋千OA静止的时候，踏板离地高一尺（AC＝1尺），将它往前推进两步（EB＝10尺），此时踏板升高离地五尺（BD＝5尺），求秋千绳索（OA或OB）的长度．
57．（2021秋•泗洪县期末）【直观想象】如图1，动点P在数轴上从负半轴向正半轴运动，点P到原点的距离先变小再变大，当点P的位置确定时，点P到原点的距离也唯一确定；
【数学发现】当一个动点P（x，0）到一个定点的距离为d，我们发现d是x的函数；
【数学理解】（1）动点P（x，0）到定点A（2，0）的距离为d，当x＝ 时，d取最小值；
【类比迁移】（2）设动点P（x，0）到两个定点M（1，0）、N（3，0）的距离和为y．
①随着x增大，y怎样变化？
②在给出的平面直角坐标系中画出y关于x的函数图象；
③当y＞6时，x的取值范围是 ．
58．（2021秋•海陵区校级期末）设一次函数y＝k1x+b1（k1≠0）的图象为l1，一次函数y＝k2x+b2（k2≠0）的图象为直线l2，若k1＝k2，且b1≠b2，我们就称直线l1与直线l2互相平行．解答下面的问题：
（1）求过点P（1，4）且与已知直线y＝﹣2x﹣1平行的直线l的函数表达式，并画出直线l的图象；
（2）设（1）中的直线l分别与x轴、y轴交于A、B两点，直线y＝﹣2x﹣1分别与x轴、y轴交于C、D两点，求四边形ABCD的面积．
59．（2021秋•阜宁县期末）已知：如图，E在△ABC的边AC上，且∠AEB＝∠ABC．
（1）求证：∠ABE＝∠C；
（2）若∠BAE的平分线AF交BE于点F，FD∥BC交AC于点D，设AB＝8，AC＝10，求DC的长．
60．（2021秋•滨海县期末）如图，在平面直角坐标系中，点A坐标为（6，0），在B在y轴的正半轴上，且S△AOB＝24．
（1）求点B坐标；
（2）若点P从B出发沿y轴负半轴运动，速度每秒2个单位，运动时间t秒，△AOP的面积为S，求S与t的关系式，并直接写出t的取值范围；
（3）在（2）的条件下，若S△AOP：S△ABP＝1：3，且S△AOP+S△ABP＝S△AOB，在线段AB的垂直平分线上是否存在点Q，使得△AOQ的面积与△BPQ的面积相等？若存在，求出Q点坐标；若不存在，请说明理由．