2022-2023学年四川省成都外国语学校高二上学期期中考试数学（理）试题（解析版）

这是一份2022-2023学年四川省成都外国语学校高二上学期期中考试数学（理）试题（解析版），共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
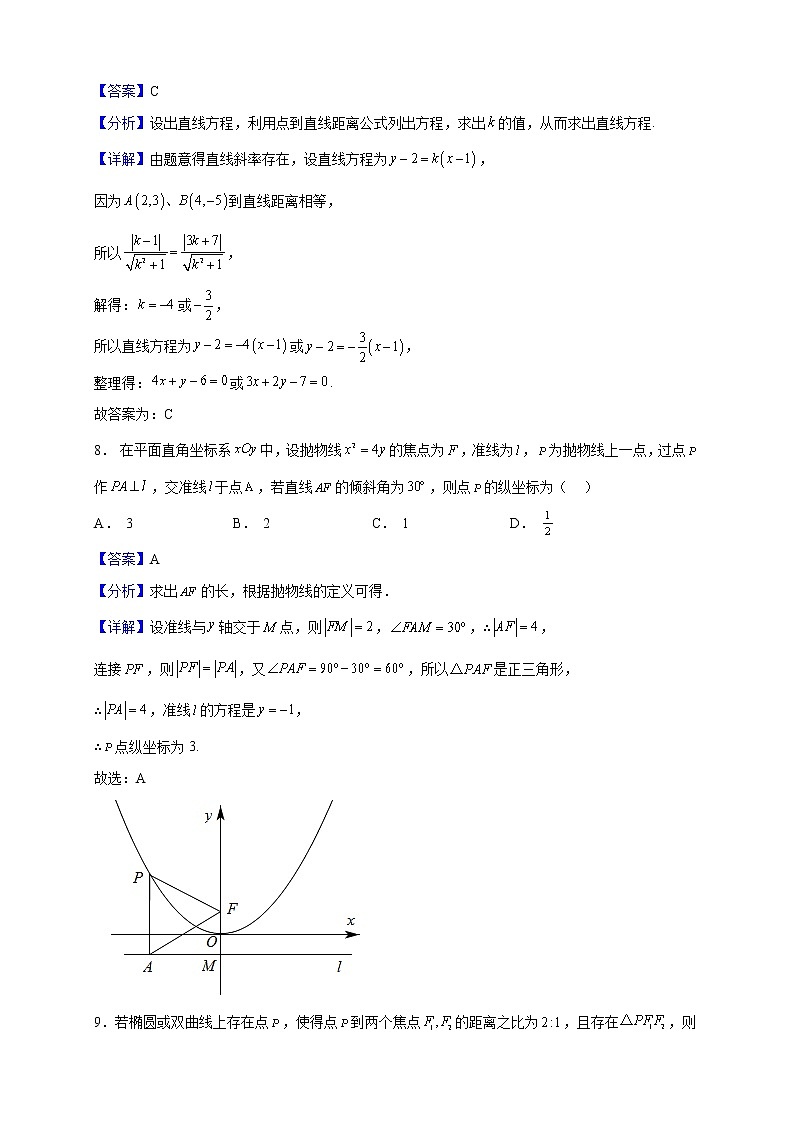
2022-2023学年四川省成都外国语学校高二上学期期中考试数学（理）试题 一、单选题1．在空间直角坐标系，点关于xOy平面的对称点B的坐标为（    ）．A． B． C． D．【答案】C【分析】由空间直角坐标中的点关于面对称求对称点坐标.【详解】由与关于xOy平面对称，且，所以.故选：C2．已知双曲线的渐近线方程是（    ）A． B． C． D．【答案】C【分析】根据给定的双曲线方程，直接求出渐近线方程作答.【详解】依题意，双曲线的焦点在y轴上，实半轴长，虚半轴长，所以双曲线的渐近线方程是.故选：C3．已知圆与圆外切，则m的值为（    ）A．1 B．9 C．10 D．16【答案】B【分析】直接利用圆心距等于两圆的半径之和列方程即可求解.【详解】因为圆C与圆O外切，所以两圆的圆心距等于两圆的半径之和，即，解得．故选：B．4．已知直线：与直线：垂直，则实数的值为（    ）A． B．C．或 D．不存在【答案】C【分析】根据直线垂直的关系即得.【详解】由两直线垂直可得，解得或.故选：C.5．如果方程表示焦点在轴上的椭圆，则实数的取值范围是（    ）A． B．C．或 D．且【答案】D【分析】依题意可得，即可求出参数的取值范围.【详解】因为方程表示焦点在轴上的椭圆，所以，即，解得且；故选：D.6．已知双曲线上一点P到焦点的距离为9，则它到另一个焦点的距离为（    ）A．15 B．5 C．3或5 D．3或15【答案】D【分析】根据双曲线的定义进行求解即可.【详解】由双曲线的定义可知，而，所以，或，由，双曲线上的点到焦点的距离最小值为，显然 和都符合题意，故选：D7．过点引直线，使到它的距离相等，则此直线方程为（    ）A． B．C．或 D．或【答案】C【分析】设出直线方程，利用点到直线距离公式列出方程，求出的值，从而求出直线方程.【详解】由题意得直线斜率存在，设直线方程为，因为到直线距离相等，所以，解得：或，所以直线方程为或，整理得：或.故答案为：C8． 在平面直角坐标系中，设抛物线的焦点为，准线为，为抛物线上一点，过点作，交准线于点，若直线的倾斜角为，则点的纵坐标为（    ）A． 3     B． 2     C． 1     D． 【答案】A【分析】求出的长，根据抛物线的定义可得．【详解】设准线与轴交于点，则，，∴，连接，则，又，所以是正三角形，∴，准线的方程是，∴点纵坐标为3.故选：A9．若椭圆或双曲线上存在点，使得点到两个焦点的距离之比为，且存在，则称此椭圆或双曲线存在“点”，下列曲线中存在“点”的是（    ）A． B． C． D．【答案】C【分析】求出满足条件时的和，再求出，验证，，能否是三角形的三边长，即可得．【详解】，则，若是椭圆，则，，，若是双曲线，则，，A中椭圆，，，，，不存在；B中椭圆，，，，，不存在C中双曲线，，双曲线上点到到右焦点距离的最小值是，，，，构成，存在“点”，D中双曲线，，，，，，不存在故选：C．【点睛】本题考查新定义“点”，解题方法是弱化条件，求出满足部分条件的点具有的性质，验证是否满足另外的条件：构成三角形．从而完成求解．10．已知，，分别为椭圆C：的左，右焦点，过垂直于长轴的直线交椭圆C于A、B两点，且；Q为C上任意一点，求的最小值为（    ）A．3 B．4 C．5 D．6【答案】A【分析】先求出椭圆的方程，再根据椭圆的定义将的最小值转化为的最小值，从而可得正确的选项.【详解】连接，由椭圆方程可得，故在椭圆方程，令，则，因为，故，解得，故椭圆方程为：.而，因为，故，当且仅当三点共线且在中间时等号成立，故即的最小值为3.故选：A.【点睛】关键点睛：利用椭圆的定义是解题的关键.11．3D打印是快速成型技术的一种，它是一种以数字模型文件为基础，运用粉末状金属或塑料等可粘合材料，通过逐层打印的方式来构造物体的技术，如图所示的塔筒为3D打印的双曲线型塔筒，该塔筒是由离心率为的双曲线的一部分围绕其旋转轴逐层旋转打印得到的，已知该塔筒（数据均以外壁即塔筒外侧表面计算）的上底直径为4cm，下底直径为6cm，高为9cm，则喉部（最细处）的直径为（    ）A．cm B．cm C．cm D．cm【答案】D【分析】作该塔筒的轴截面图像并建立坐标系，根据双曲线的性质求出其实轴长度即可.【详解】该塔筒的轴截面如图所示，以C为喉部对应点，设A与B分别为上、下底面对应点，以双曲线的对称中心为原点，焦点所在轴为x轴建立如图所示的坐标系.由题意可知，，，设，则．设双曲线的方程为，∵双曲线的离心率为，∴．方程可化简为(*)，将A和B的坐标代入(*)式可得解得，则喉部的直径cm．故选：D12．在平面直角坐标系xOy中，若抛物线C:y2=2px()的焦点为F，直线x=3与抛物线C交于A，B两点，｜AF|=4，圆E为的外接圆，直线OM与圆E切于点M，点N在圆E上，则的取值范围是（    ）A． B． C． D．【答案】B【分析】由已知及抛物线的定义，可求，进而得抛物线的方程，可求，，的坐标，直线的方程，可得圆的半径，求得圆心，设的坐标，求得的坐标，结合向量数量积的坐标表示，以及辅助角公式和正弦函数的值域，可得所求范围．【详解】解：由题意，设，所以，解得，所以抛物线的方程为，，，，所以直线的方程为，设圆心坐标为，，所以，解得，即，圆的方程为，不妨设，设直线的方程为，则，根据，解得，由，解得，设，所以，因为，所以．故选：B．【点睛】关键点点睛：本题解题的关键点是：首先求出圆的方程为，然后利用直线OM与圆E切于点M，求出M点的坐标，引入圆的参数方程表示N点坐标，再根据向量数量积的坐标表示及辅助角公式，可得所求范围．. 二、填空题13．抛物线的焦点坐标为_____．【答案】【分析】由抛物线的性质即可得出答案.【详解】由抛物线方程知，抛物线焦点在y轴上，由，得，所以焦点坐标为．故答案为：.14．过椭圆的一个焦点的弦与另一个焦点围成的的周长为___________.【答案】12【分析】求得，利用椭圆的定义可得出的周长.【详解】在椭圆中，，由题意可知，的周长为.故答案为：.15．已知倾斜角为的直线l经过抛物线的焦点交抛物线于A、B两点，并且，则______．【答案】##【分析】根据抛物线的定义，结合正弦函数的定义进行求解即可.【详解】若角为锐角，如图，设A、B两点在准线上的射影分别为C、D．过B作于则有，设，则．由勾股定理可知：则．若角为钝角，由对称性可知，故答案为：．16．已知，分别为双曲线的左、右焦点，点P在双曲线上且不与顶点重合，满足，该双曲线的离心率为___________________．【答案】2【分析】首先确定P点在左支上，作出的内切圆M，内切圆M切于A点，证明点A为双曲线的左顶点，从而根据得到，从而得到，求出离心率.【详解】因为，所以，所以，故P点在左支上，作的内切圆M，设内切圆M与切于点C，与切于点B，该内切圆M切于A点，连接，则，且平分，平分，接下来证明点A为双曲线的左顶点，由双曲线的定义可知：，因为，所以，设点A坐标为，则，解得：，故点A为双曲线的左顶点，∵，∴，∴∴，∴，∴，∴．故答案为：2 三、解答题17．已知关于，的方程.（1）若方程表示圆，求的取值范围；（2）当时，曲线与直线相交于，两点，求的值.【答案】（1）；（2）.【解析】（1）将圆的方程化为标准形式，由求解.（2）利用点到直线的距离公式求得圆心到直线的距离，再由弦长公式求解.【详解】（1）方程可化为，因为方程表示圆，所以，解得.（2）圆的圆心，圆心到直线的距离为，圆的半径，所以.【点睛】本题主要考查圆的标准方程，点到直线的距离公式、弦长公式的应用，还考查了运算求解的能力，属于基础题.18．已知双曲线C：的离心率为，实轴长为2.(1)求双曲线的标准方程；(2)若直线被双曲线C截得的弦长为，求m的值.【答案】(1)(2) 【分析】（1）根据题意，列出关于的方程组，求得的值，即可得到双曲线的方程；（2）联立方程组，利用根与系数的关系，求得，在利用弦长公式列出方程，即可求解.【详解】（1）双曲线离心率为，实轴长为2，，，解得，，，所求双曲线C的方程为；（2）设,,联立，，，，．，，解得．19．已知抛物线上的点到焦点F的距离为6．(1)求抛物线C的方程；(2)过点作直线l交抛物线C于A，B两点，且点P是线段的中点，求直线l方程．【答案】(1).(2). 【分析】（1）由抛物线定义有求参数，即可写出抛物线方程.（2）由题意设，联立抛物线方程，结合韦达定理、中点坐标求参数k，即可得直线l方程．【详解】（1）由题设，抛物线准线方程为，∴抛物线定义知：，可得，∴.（2）由题设，直线l的斜率存在且不为0，设，联立抛物线方程，有，整理得，则，又P是线段的中点，∴，即，故.20．已知椭圆C： (a＞b＞0)的两个焦点分别为F1、F2，短轴的一个端点为P．（1）若∠F1PF2为直角，焦距长为2，求椭圆C的标准方程；（2）若∠F1PF2为钝角，求椭圆C的离心率的取值范围．【答案】（1）；（2）.【解析】（1）由题意知为等腰直角三角形，且焦距长为2，即可求出，写出椭圆方程即可.（2）由∠F1PF2为钝角，即有sin∠OPF2＝，结合椭圆离心率性质即可求出离心率的取值范围.【详解】（1）因为椭圆短轴的一个端点为P，且∠F1PF2为直角，知b＝c，a＝c，由焦距长为2，所以c＝1， a＝ ，b＝1，∴椭圆C的标准方程为． （2）因为椭圆短轴的一个端点为P，且∠F1PF2为钝角，即45°＜∠OPF2＜90°，所以sin∠OPF2＝，又因为椭圆的离心率e∈(0,1)，所以椭圆C的离心率的取值范围为．21．已知平面内一动点到点的距离比到轴的距离大1．(1)求动点的轨迹的方程；(2)过点的直线交曲线C于A、B，且有 ，求直线的斜率．【答案】(1)；(2). 【分析】（1）根据两点间距离公式，结合已知进行求解即可；（2）根据一元二次方程根与系数关系、根的判别式，结合平面向量共线的性质进行求解即可.【详解】（1）因为平面内一动点到点的距离比到轴的距离大1，所以有；（2）当直线AB的斜率不存在时，把代入中，得，因为 ，所以不成立，不符合题意；当直线AB的斜率存在时，设，与抛物线方程联立：，化简整理，得：，有，且，,，而，解得：，而，即：，化简整理，得：.【点睛】关键点睛：由平面向量共线的性质得到之间的关系是解题的关键.22．已知椭圆的左、右焦点分别为，，为椭圆上一动点，当的面积最大时，其内切圆半径为，椭圆的长轴长为4．(1)求椭圆C的方程；(2)是否存在⊙O：，使得⊙O的任意切线l与椭圆交于A，B两点，都有．若存在，求出r的值，并求此时△AOB的面积S的取值范围；若不存在，请说明理由.【答案】(1)；(2)存在，. 【分析】（1）根据椭圆的定义，结合三角形内切圆的性质进行求解即可；（2）根据圆的切线性质，结合平面向量互相垂直的性质、一元二次方程根与系数关系分类讨论进行求解即可.【详解】（1），显然当与上（下）顶点重合时，的面积最大，所以有，因为椭圆的长轴长为4，所以，于是有，所以椭圆C的方程为；（2）假设存在⊙O：满足题意，①切线方程l的斜率存在时，设切线方程l：y＝kx＋m与椭圆方程联立，消去y得，(*)设，，由题意知，(*)有两解所以，即由根与系数的关系可得，所以因为，所以，即化简得，且，O到直线l的距离所以，又，此时，所以满足题意所以存在圆的方程为⊙O：．△AOB的面积，又因为当k≠0时当且仅当即时取等号．又因为，所以，所以．当k＝0时，②斜率不存在时，直线与椭圆交于两点或两点．易知存在圆的方程为⊙O：且．综上，所以．【点睛】关键点睛：根据平面向量互相垂直的性质，结合一元二次方程根与系数关系是解题的关键.