初中数学华师大版八年级下册第19章 矩形、菱形与正方形19.1 矩形2. 矩形的判定精品习题

这是一份初中数学华师大版八年级下册第19章 矩形、菱形与正方形19.1 矩形2. 矩形的判定精品习题，共9页。试卷主要包含了对角线相等且互相平分的四边形是，下列命题中，假命题是，下列关于矩形的说法中正确的是等内容，欢迎下载使用。
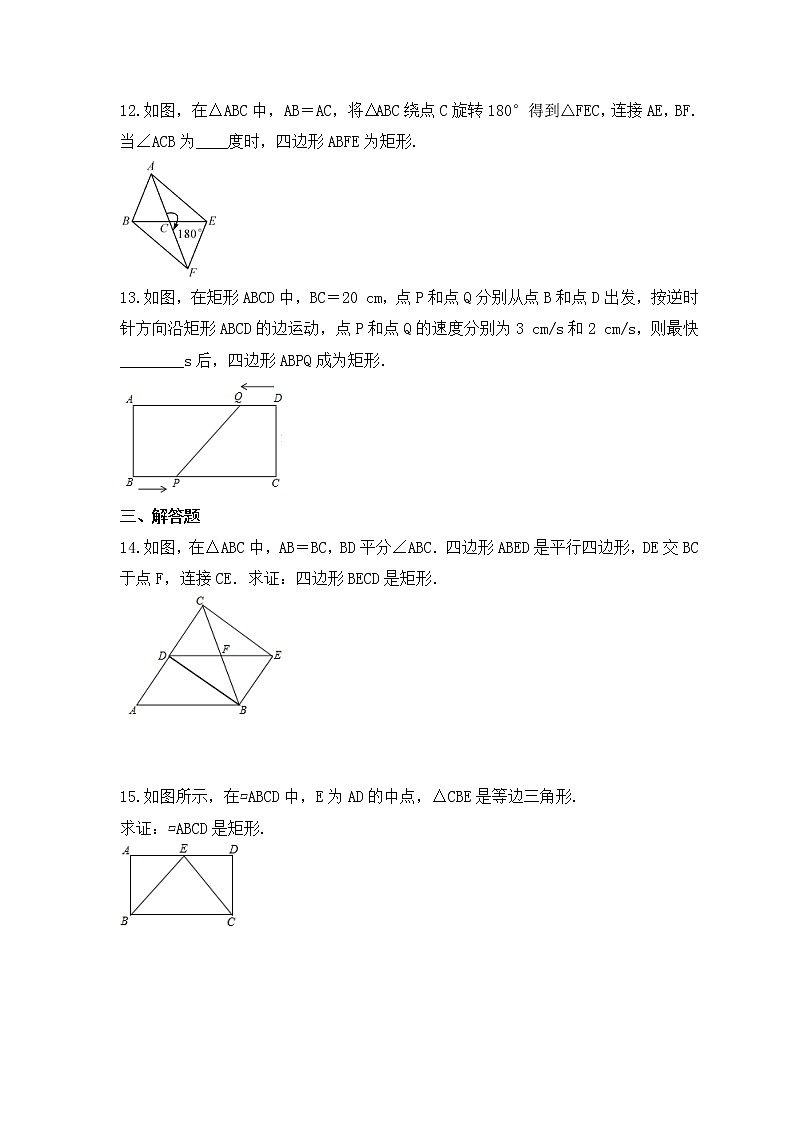
华师大版数学八年级下册课时练习19.1.2《矩形的判定》一              、选择题1.对角线相等且互相平分的四边形是(  　　)A.一般四边形                     B.平行四边形                        C.矩形                       D.菱形2.在▱ABCD中，AC交BD于点O，再添加一个条件，仍不能判定四边形ABCD是矩形的条件是(    )A.AB＝AD           B.OA＝OB             C.AC＝BD              D.DC⊥BC3.在四边形ABCD中，AC与BD相交于点O，且OA＝OC，OB＝OD.如果再增加条件AC＝BD，此四边形一定是(　　)A.正方形                      B.矩形                         C.菱形                        D.都有可能4.在四边形ABCD中，AC、BD交于点O，在下列各组条件中，不能判定四边形ABCD为矩形的是(　　)A.AB＝CD，AD＝BC，AC＝BDB.AO＝CO，BO＝DO，∠A＝90°C.∠A＝∠C，∠B＋∠C＝180°，AC⊥BDD.∠A＝∠B＝90°，AC＝BD5.下列命题中，假命题是(　　)A.有一组对角是直角且一组对边平行的四边形是矩形B.有一组对角是直角且一组对边相等的四边形是矩形C.有两个内角是直角且一组对边平行的四边形是矩形D.有两个内角是直角且一组对边相等的四边形是矩形6.如图，四边形ABCD为平行四边形，延长AD到E，使DE＝AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是(　　)A.AB＝BE                          B.BE⊥DC                     C.∠ADB＝90°                       D.CE⊥DE 7.下列关于矩形的说法中正确的是(　　)A.对角线相等的四边形是矩形B.矩形的对角线相等且互相平分C.对角线互相平分的四边形是矩形D.矩形的对角线互相垂直且平分8.如图，在△ABC中，AB＝6，AC＝8，BC＝10，P为边BC上一动点(且点P不与点B、C重合)，PE⊥AB于E，PF⊥AC于F，M为EF中点.设AM的长为x，则x的取值范围是(　　)A.4≥x＞2.4      B.4≥x≥2.4    C.4＞x＞2.4     D.4＞x≥2.4二              、填空题9.如图所示，已知▱ABCD，下列条件：①AC＝BD，②AB＝AD，③∠1＝∠2，④AB⊥BC中，能说明▱ABCD是矩形的有(填写序号)　　　　　　．　10.如图，在△ABC中，AB=AC，将△ABC绕点C旋转180°得到△FEC，连接AE，BF.当∠ACB为__________度时，四边形ABFE为矩形.11.如图，已知MN∥PQ，EF与MN、PQ分别交于A、C两点，过A、C两点作两组内错角的平分线，交于B、D，则四边形ABCD是________．12.如图，在△ABC中，AB＝AC，将△ABC绕点C旋转180°得到△FEC，连接AE，BF.当∠ACB为____度时，四边形ABFE为矩形.13.如图，在矩形ABCD中，BC＝20 cm，点P和点Q分别从点B和点D出发，按逆时针方向沿矩形ABCD的边运动，点P和点Q的速度分别为3 cm/s和2 cm/s，则最快________s后，四边形ABPQ成为矩形．　三              、解答题14.如图，在△ABC中，AB＝BC，BD平分∠ABC．四边形ABED是平行四边形，DE交BC于点F，连接CE．求证：四边形BECD是矩形．  15.如图所示，在▱ABCD中，E为AD的中点，△CBE是等边三角形.求证：▱ABCD是矩形.   16.如图，在▱ABCD中，DE⊥AB，BF⊥CD，垂足分别为E，F．(1)求证：△ADE≌△CBF；(2)求证：四边形BFDE为矩形．    17.如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交CE的延长线于点F，且AF＝BD，连接BF．(1)求证D是BC的中点；(2)如果AB＝AC，试判断四边形AFBD是什么四边形，并证明你的结论．   18.如图，▱ABCD的对角线AC、BD相交于点O，AE＝CF.(1)求证：△BOE≌△DOF；(2)若BD＝EF，连接DE、BF，判断四边形EBFD的形状，并证明你的结论.    19.如图，在▱ABCD中，E是AD上一点，连接BE，F为BE中点，且AF＝BF，(1)求证：四边形ABCD为矩形；(2)过点F作FG⊥BE，垂足为F，交BC于点G，若BE＝BC，S△BFG＝5，CD＝4，求CG．      20.如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC.设MN交∠ACB的角平分线于点E，交∠ACB的外角角平分线于点F.(1)求证：OE＝OF；(2)若CE＝12，CF＝5，求OC的长；(3)当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由.
答案1.C.2.A3.B.4.C.5.C.6.B.7.B.8.C.9.答案为：①④.10.答案为：60．11.答案为：矩形.12.答案为：60．13.答案为：4.14.证明：∵AB＝BC，BD平分∠ABC，∴BD⊥AC，AD＝CD．∵四边形ABED是平行四边形，∴BE∥AD，BE＝AD，∴BE＝CD，∴四边形BECD是平行四边形．∵BD⊥AC，∴∠BDC＝90°，∴▱BECD是矩形．15.证明：∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC，AB＝DC，∴∠D＋∠A＝180°，∵E是AD边的中点，∴AE＝DE，∵△CBE是等边三角形，∴BE＝CE，在△ABE和△DCE中，AB＝DC；AE＝DE；BE＝CE，∴△ABE≌△DCE(SSS)，∴∠A＝∠D，∵∠D＋∠A＝90°，∴∠D＝∠A＝90°，∵四边形ABCD是平行四边形，∴▱ABCD是矩形.16.证明：(1)∵DE⊥AB，BF⊥CD，∴∠AED＝∠CFB＝90°，∵四边形ABCD为平行四边形，∴AD＝BC，∠A＝∠C，在△ADE和△CBF中，，∴△ADE≌△CBF(AAS)；(2)∵四边形ABCD为平行四边形，∴CD∥AB，∴∠CDE＋∠DEB＝180°，∵∠DEB＝90°，∴∠CDE＝90°，∴∠CDE＝∠DEB＝∠BFD＝90°，则四边形BFDE为矩形．17.证明：(1)∵AF∥BD，∴∠AFE＝∠DCE．∵E是AD的中点，∴AE＝DE．  又∵∠AEF＝∠DEC，∴△AEF≌△DEC(AAS)． ∴DC＝AF．  又∵AF＝BD，∴BD＝DC．∴D是BC的中点．     (2)四边形AFBD是矩形．  证明：∵AF＝BD，AF∥BD， ∴四边形AFBD是平行四边形．   ∵AB＝AC，D是BC的中点，∴AD⊥BC，∴∠ADB＝90°．  ∴四边形AFBD是矩形．18.证明：(1)∵四边形ABCD是平行四边形，∴BO＝DO，AO＝OC，∵AE＝CF，∴AO﹣AE＝OC﹣CF，即：OE＝OF，在△BOE和△DOF中，∴△BOE≌△DOF(SAS)；(2)矩形，证明：∵BO＝DO，OE＝OF，∴四边形BEDF是平行四边形，∵BD＝EF，∴平行四边形BEDF是矩形.19.证明：(1)∵F为BE中点，AF＝BF，∴AF＝BF＝EF，∴∠BAF＝∠ABF，∠FAE＝∠AEF，在△ABE中，∠BAF＋∠ABF＋∠FAE＋∠AEF＝180°，∴∠BAF＋∠FAE＝90°，又四边形ABCD为平行四边形，∴四边形ABCD为矩形.(2)解：连接EG，过点E作EH⊥BC，垂足为H，∵F为BE的中点，FG⊥BE，∴BG＝GE，∵S△BFG＝5，CD＝4，∴S△BGE＝10＝0.5BGEH，∴BG＝GE＝5，在Rt△EGH中，GH＝3，在Rt△BEH中，BE＝4＝BC，∴CG＝BC﹣BG＝4﹣5．20.证明：(1)∵CF平分∠ACD，且MN∥BD，∴∠ACF＝∠FCD＝∠CFO.∴OF＝OC，同理可证：OC＝OE，∴OE＝OF.(2)由(1)知：OF＝OC，OC＝OE，∴∠OCF＝∠OFC，∠OCE＝∠OEC.∴∠OCF＋∠OCE＝∠OFC＋∠OEC，而∠OCF＋∠OCE＋∠OFC＋∠OEC＝180°，∴∠ECF＝∠OCF＋∠OCE＝90°，∴EF＝13.∴OC＝EF＝6.5.(3)当点O移动到AC中点时，四边形AECF为矩形.理由：由(1)知OE＝OF，当点O移动到AC中点时有OA＝OC，∴四边形AECF为平行四边形.又∵∠ECF＝90°，∴四边形AECF为矩形.