人教版七年级下册第五章 相交线与平行线5.3 平行线的性质5.3.2 命题、定理、证明教学课件ppt

这是一份人教版七年级下册第五章 相交线与平行线5.3 平行线的性质5.3.2 命题、定理、证明教学课件ppt，共24页。PPT课件主要包含了知识要点，真命题与假命题，定理与证明，4直角都相等，等边三角形，同位角相等，两直线平行，假命题，真命题，画出图形等内容，欢迎下载使用。

（1）三角形的内角和等于180°;
（2）如果两个角是对顶角，那么这两个角相等;
（3）两直线平行，同旁内角相等;
（5）经过一点确定一条直线.
如果两个角是对顶角，那么这两个角相等;
两直线平行，同旁内角相等;
（6）取线段AB的中点C.
（1）长度相等的两条线段是相等的线段吗?
（2）两条直线相交，有且只有一个交点；
（3）不相等的两个角不是对顶角；
（4）欢迎前来参加北京冬奥会！
（5）两个锐角的和是钝角；
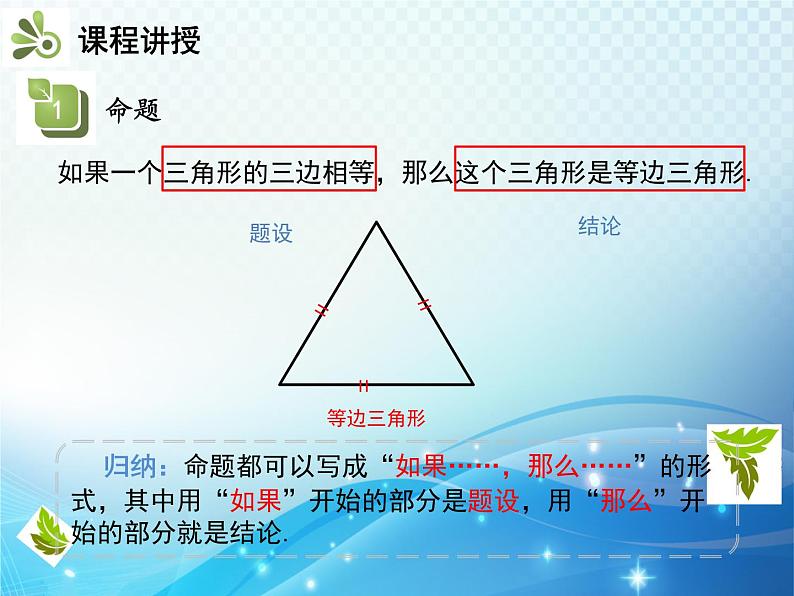
如果一个三角形的三边相等，那么这个三角形是等边三角形.
⑴同位角相等，两直线平行；
　　如果同位角相等，那么两直线平行.
⑵三个角都相等的三角形是等边三角形.
这个三角形是等边三角形
一个三角形的三个角相等
　　如果一个三角形的三边相等，那么这个三角 　形是等边三角形.
（6）两点之间线段最短；
（1）一个角的补角大于这个角；
（2）相等的两个角是对顶角；
（3）两点可以确定一条直线；
（4）若A=B，则2A=2B；
（5）锐角和钝角互为补角；
定义：数学中这些命题的正确性是人们在长期实践中总结出来的，并把它们作为判断其他命题真假的原始依据，即出发点.这样的真命题视为基本事实.我们也称它为公理.
3.全等三角形的对应边、对应角分别相等．
1.一条直线截两条平行直线所得的同位角相等；
2.两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行；
定义： 数学中，有些命题可以从基本事实或其他真命题出发，用逻辑推理的方法判断它们是正确的，并且可以作为进一步判断其他命题真假的依据，这样的真命题叫做定理.
比如:“内错角相等,两直线平行”这条定理就是在“同位角相等,两直线平行”这条公理的基础上推理而出的,它又可以作为判定平行线的依据.
基本事实、定理、命题的关系：
基本事实（正确性由实践总结）
定理（正确性通过推理证实）
已知直线b∥c， a⊥b ．求证：a⊥c．
证明：∵ a ⊥b（已知），
∴ ∠1=90°（垂直的定义）.
∵ b ∥ c（已知），∴∠1=∠2（两直线平行，同位角相等），
∴ ∠2=∠1=90°（等量代换），
∴ a ⊥ c（垂直的定义）.
已知：如图，直线l3分别与l1，l2交于点A,点B，且∠1=∠2.
证明：∵　∠１=∠２　
(同位角相等,两直线平行).
１．下列句子中，哪些是命题？哪些不是命题？⑴对顶角相等；⑵画一个角等于已知角；⑶两直线平行，同位角相等；⑷a，b两条直线平行吗？⑸温柔的李明明；⑹玫瑰花是动物；⑺若a2＝4，求a的值；⑻若a2＝ b2，则a＝b.
2.把下列命题改写成“如果……，那么……”的形式，并分别指出它的题设和结论：
全等三角形的对应边相等；
这两个三角形的对应边相等
如果两个三角形全等，那么它们的对应边相等
3.指出下列命题中的真命题和假命题：
（1）同位角相等，两直线平行；（2）多边形的内角和等于180°；（3）三角形的外角和等于360°；（4）平行于同一条直线的两条直线互相平行.
4.求证：邻补角的平分线互相垂直．
已知：如图，∠AOB＋∠BOC＝180°，OE平分∠AOB，OF平分∠BOC．
∴OE⊥OF（垂直定义）．
表示判断的语句叫做命题.
如果题设成立，那么结论一定成立.像这样的命题，称为真命题.
当题设成立时，不能保证结论总是正确，或者说结论不成立，像这样的命题，称为假命题.