






二次函数的最值问题 课件-2022年浙江省中考数学一轮复习(浙教版)
展开
这是一份二次函数的最值问题 课件-2022年浙江省中考数学一轮复习(浙教版),共19页。PPT课件主要包含了问题背景,好呀好呀,问题探究,哪个变量作为自变量,实际问题,模型思想,数形结合思想,AD或AB,顶点式,一般式等内容,欢迎下载使用。
小明,我们家打算在山那边建个果园,增加收入,你说好不好呀?
小明,我们这个果园一面靠着山脚的一堵墙,其余三面用围栏围起来,围栏的总长度为197米,而且还要开个门,你说怎么围才能使果园的面积最大呢?
利用一堵墙(墙EF足够长),用197米长的围栏围成一个矩形果园ABCD,与墙平行的一边BC上要预留3米宽的入口(如图中MN所示,不用围栏).那怎么围才能使矩形果园ABCD的面积最大,面积最大值是多少平方米?
问题1 你要求的是什么?即目标是什么?
矩形果园ABCD面积的最大值.
问题2 矩形果园ABCD面积怎么求?
矩形果园ABCD的面积=长×宽=BC×AB.
问题3 在这个等量关系中有几个变量?
问题4 如果设AB为x米,那么你能用x表示BC吗?
BC为(200-2x)米.
解:设矩形果园ABCD的面积为S平方米,AB为x米,则BC为(200-2x)米.∴S=x(200-2x)=-2x2+200x =-2(x-50)2+5000.∴当x=50时,S取到最大值,最大值为5000平方米.答:与墙垂直的一边AB为50米,矩形果园ABCD的面积最大,最大值是5000平方米.
问题5 回顾解题过程,你还有什么疑惑吗?
AB一定能取到50米吗?
解:设矩形果园ABCD的面积为S平方米,AB为x米,则BC为(200-2x)米.∴S=x(200-2x)=-2x2+200x =-2(x-50)2+5000.由题意得∴ .∴当x=50时,S取到最大值,最大值为5000平方米.答:与墙垂直的一边AB为50米,矩形果园ABCD的面积最大,最大值是5000平方米.
问题6 求自变量的取值范围时要考虑哪些方面?
①使函数表达式有意义;②使实际问题有意义.
①找出实际问题中要求最值的量所在的等量关系;②判断等量关系中的变量个数,确定自变量;③设要求最值的量为函数y,自变量为x,用x表示其余变量;④根据等量关系列出二次函数表达式.
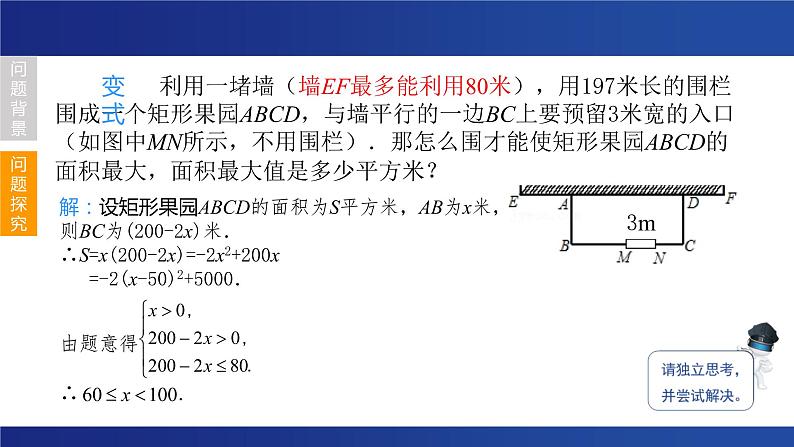
利用一堵墙(墙EF最多能利用80米),用197米长的围栏围成一个矩形果园ABCD,与墙平行的一边BC上要预留3米宽的入口(如图中MN所示,不用围栏).那怎么围才能使矩形果园ABCD的面积最大,面积最大值是多少平方米?
解:设矩形果园ABCD的面积为S平方米,AB为x米,则BC为(200-2x)米.∴S=x(200-2x)=-2x2+200x =-2(x-50)2+5000.由题意得∴ .
问题7 观察函数图象,并说一说二次函数的最值在自变量的哪些值取到?
如图所示,如果二次函数有最值,最值对应的自变量的值要么是顶点的横坐标,要么是自变量范围的端点值.
步骤:①写出二次函数表达式并求出对称轴;②求出自变量的取值范围;③判断顶点的横坐标是否在自变量的取值范围内;④利用图象和性质求出最值.
小明,数学可以帮助我们解决很多实际问题呢!
比如我们家的窗户当时用的材料是6米,那怎么改进设计才能使窗户的透光面积最大呢?
例 如图,小明家窗户的上部是由两个正方形组成的矩形,窗框材料总长为6米,如何改进设计才能使窗户透光面积最大,最大面积是多少平方米(保持窗户的样式不变)?
窗户透光面积的最大值.
问题2 窗户透光面积怎么求?
窗户透光面积=长×宽=AD×AB.
问题4 如果设AB为x米,那么你能用x表示AD吗?
小明,果子成熟了,我准备采摘下来送到市场上去卖。
拓展 某种水果的成本价是2元/千克,如果以每千克4元的价格出售,每天可售出100千克.通过调查发现,这种水果每千克的售价每降低0.1元,每天可多售出20千克,为保证每天至少售出260千克,小明爸爸决定降价销售.那么小明爸爸应该如何确定这批水果的销售价格,才能使日销售利润最大,利润最大值是多少元?
问题2 日销售利润怎么求?与其它量之间有什么等量关系?
日销售利润=(每千克的销售价格-每千克的成本价格)×日销售量.
销售价格或降低的价格.
问题4 如果设销售价格为x元/千克,那么你能用x表示日销售量吗?
日销售量为[100+200(4-x)]千克.
∵w=(x-2)(900-200x)=-200(x-2)(x-4.5),
解:设日销售利润为w元,销售价格为x元/千克.由题意得 ∴ .
相关课件
这是一份(经典版)中考数学一轮考点复习精品课件专题3.5 二次函数的最值问题 (含解析),共25页。PPT课件主要包含了拓展训练,h≥3,∵y轴为对称轴,∴a0,∴b2a2+4a,∴对称轴为x-2,yax2+bx+c,D定点,8-x,-25或8等内容,欢迎下载使用。
这是一份二次函数综合问题之线段问题-中考数学一轮复习课件,共19页。PPT课件主要包含了经典例题分析等内容,欢迎下载使用。
这是一份(通用版)中考数学一轮复习练习课件专题3.5 二次函数的最值问题 (含答案),共25页。PPT课件主要包含了拓展训练,h≥3,∵y轴为对称轴,∴a0,∴b2a2+4a,∴对称轴为x-2,yax2+bx+c,D定点,8-x,-25或8等内容,欢迎下载使用。









