









九年级下册26.3 实践与探索优秀课件ppt
展开26.3 实践与探索
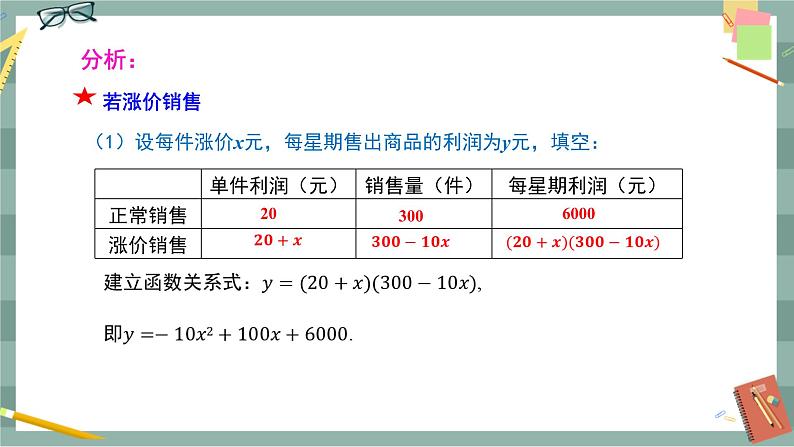
第2课时 商品销售最大利润问题
同步练习
1.某民俗旅游村为满足游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出.若每张床位每天收费提高20元,则相应减少10张床位租出.如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A.140元 B.160元 C.180元 D.200元
2.某产品进货单价为90元,按100元一件出售时,能售出500件.若每件涨价1元,则销售量就减少10件,则该产品能获得的最大利润为( )
A.5 000元 B.8 000元
C.9 000元 D.10 000元
3.某网店销售某种商品,成本为30元/件,当销售价格为60元/件时, 每天可售出100件,经市场调查发现,销售单价每降1元,每天销量增加10件,在保证盈利的情况下,当销售单价为 元时,每天获取的利润最大.
4.某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx75,其图象如图所示.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?
参考答案
1.B
2.C 解析:设单价为x元,总利润为W元,
则可得销量为500-10(x-100),单件利润为(x-90)元,
根据题意,得W=+9 000,故可得当x=120时,W有最大值,最大值为9 000.
3.50 解析:若设每件降价x元,每天售出商品的利润为y元,根据题意,得y=(60-x-30)(100+10x)=-10x2+200x+3 000=-10+4 000.
∵ 60-x-30>0,且x≥0,∴ 0≤x<30.
∴ 当x=10时,y取得最大值,最大值为4 000.
即当降价10元时,也就是当销售单价为50元时,每天获取的利润最大.
4.解:(1)由图象可得函数图象过点(5,0),(7,16),
代入,得y=-x2+20x-75.
∵ -1<0,图象对称轴为直线x=10,
∴ 当x=10时,y值最大,最大值为25.
即销售单价为10元时,销售利润最大,最大利润为25元.
(2)由对称性知y=16时,x=7和13,故销售单价在7≤x≤13时,每天的销售利润不低于16元.
初中数学26.3 实践与探索精品ppt课件: 这是一份初中数学26.3 实践与探索精品ppt课件,共23页。PPT课件主要包含了复习引入,x≤2,0-6,x-6或x1,x1-4x22,x-4或x2,x-1,合作探究,x2h,方法二等内容,欢迎下载使用。
数学华师大版26.3 实践与探索精品课件ppt: 这是一份数学华师大版26.3 实践与探索精品课件ppt,文件包含263实践与探索2课件pptx、263实践与探索2教案docx等2份课件配套教学资源,其中PPT共28页, 欢迎下载使用。
初中数学26.3 实践与探索一等奖课件ppt: 这是一份初中数学26.3 实践与探索一等奖课件ppt,文件包含263实践与探索1课件pptx、263实践与探索1教案docx等2份课件配套教学资源,其中PPT共32页, 欢迎下载使用。













