初中数学3. 切线优质课件ppt

教学目标

1.掌握切线的判定定理与切线的性质定理.

2. 能够运用切线的判定方法判断一条直线是否为圆的切线；会过圆上一点画圆的切线.

3.会运用圆的切线的判定与性质来解决相关问题.

教学重难点

重点：理解并掌握圆的切线的判定定理与切线的性质定理.

难点：能运用圆的切线的判定定理与性质定理解决问题.

教学过程

导入新课

教师提出问题：下图中让你感受到了直线与圆的哪种位置关系？如何判断一条直线是否为切线呢？

学生回答：相切.

教师：你是怎样判断出图中的直线与圆相切的？如何界定直线与圆是否只有一个公共点？教师指出，根据切线的定义可以识别一条直线是不是圆的切线，但有时使用定义识别很不方便，为此我们还要学习识别切线的其他方法．(板书课题)              

探究新知

1. 切线的判定定理

【做一做】

如图，画一个⊙Ｏ及半径OA,经过⊙O的半径OA 的外端 A，画一条直线l

垂直于这条半径，这条直线与圆有几个公共点？

（师生互动）引导学生动手操作并思考回答.

学生：从图中可以看出，对直线l上除点Ａ外的任一点Ｐ,必有OP OA，

即点Ｐ位于圆外，从而可知直线与圆只有一个公共点，所以直线l是圆的切线.

【问题】

已知⊙O上一点A，怎样根据圆的切线定义过点A作⊙O的切线？

师生活动：学生尝试作图，教师适时点拨.

教师追问：（1）圆心O到直线AB的距离与圆的半径有什么数量关系?

（2）二者有什么位置关系？为什么？

师生活动：（小组讨论，老师点拨）抓好两个条件：①经过半径外端；②垂直于这条半径.

【归纳总结】

1.切线的判定定理：经过圆的半径的外端且垂直于这条半径的直线是圆的切线.

2.应用格式：

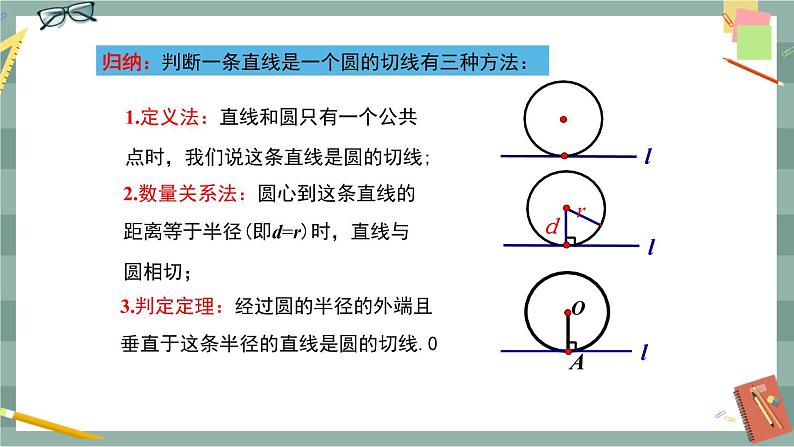
【归纳总结】 判断一条直线是一个圆的切线有三种方法：

1.定义法：直线与圆只有一个公共点时，我们说这条直线是圆的切线;

2.数量关系法：圆心到这条直线的距离等于半径(即d＝r)时，直线与

圆相切；

3.判定定理：经过圆的半径的外端且垂直于这条半径的直线是圆的切线.

【新知应用】

例 1　如图，直线AB经过⊙O上的点Ａ，且AB=OA，∠ＯBA=45°.

求证：直线AB是⊙O的切线．

【探索思路】

（学生先独立思考，教师适时点拨）由于AB经过⊙O上的点Ａ，所以OA是半径，只要证明OA⊥AB即可.

【证明】∵AB=OA，∠ＯBA=45°，

∴∠AＯB=∠ＯBA=45°，∴∠ＯAB =90°.

又∵点Ａ在⊙O上，

∴OA 是⊙O的半径，

∴直线AB是⊙O的切线．

即学即练

已知：直线AB经过⊙O上的点C，并且OA＝OB，CA＝CB.

求证：直线AB是⊙O的切线.

师生活动：学生先独立思考，教师适时点拨，由于AB过⊙O上的点C，所以连结OC，只要证明AB⊥OC即可.

【证明】连结OC.

∵ OA＝OB,CA＝CB,  

    ∴ OC是等腰三角形OAB底边AB上的中线.

∴ AB⊥OC.

    ∵ OC是⊙O的半径,

    ∴ AB是⊙O的切线.

【归纳总结】证明直线AB是⊙O的切线，有两种类型：①已知切点,连结切点与圆心，证垂直；②作垂直，证明圆心到垂足的线段长等于半径.此题是类型①，所以连结圆心与切点证垂直.

2.切线的性质定理

问题：如图，如果直线l是⊙O 的切线，点A为切点，那么OA与l垂直吗？

师生活动：（小组讨论，老师点拨）直接证明比较困难，可以运用“反证法”.

“反证法”分三步证明，即①假设原命题不成立；②在假设成立的条件下，推出矛盾；③得出结论，假设不成立.

【解】①假设OA与l不垂直,过点O作一条直线垂直于l,垂足为M.

②则OM<OA,即圆心到直线l的距离小于⊙O的半径, 因此, 直线l与⊙O相交. 这与已知条件“直线l与⊙O相切”相矛盾.

③所以⊙O的半径OA与直线l垂直.

【归纳总结】

1.切线的性质定理：圆的切线垂直于经过切点的半径.

2.应用格式

∵直线l是⊙O 的切线，A是切点，

∴直线l ⊥OA.

【新知应用】 

例2　如图, △ABC为等腰三角形，AB ＝AC，O 是底边BC的中点，腰AB与⊙O 相切于点D. 求证：AC 是⊙O 的切线.

师生活动：学生先独立思考，教师适时引导，根据切线的判定定理，要证明AC是⊙O的切线，只要证明由点O向AC所作的垂线段OE是⊙O的半径就可以了，而OD是⊙O的半径，因此只需要证明OE＝OD.

【证明】如图，过点O作OE ⊥AC,垂足为E,连结OD，OA.

∵⊙O 与AB 相切于点D，  

∴OD ⊥ AB.

又∵△ABC 为等腰三角形，O是底边BC 的中点.

∴AO 平分∠BAC，OD⊥AB，OE⊥AC，

∴OE ＝OD，

∴AC 是⊙O 的切线.

【归纳总结】证明直线AC是⊙O的切线，有两种类型：①已知切点,连结切点与圆心，证垂直；②作垂直，证明圆心到垂足的线段长等于半径.此题是类型②，所以作OE⊥AC，垂足为E，证明OE等于半径.

例3　如图，四边形OABC是平行四边形，以点O为圆心，OA为半径的圆交AB于点D，延长AO交⊙O于点E，连结CD，CE，且CE是⊙O的切线.

(1)求证：CD是⊙O的切线；

(2)若BC＝3，AB＝4，求OABC的面积.

师生活动：(引发学生思考，教师适时点拨)(1)要证明CD是切线的关键是作出正确的辅助线.(2)已知四边形OABC是平行四边形，有底边长，求其面积，还要得到哪个关键量？有切线就有垂直，利用勾股定理能得到哪条边长？

 (1)【证明】连结OD.

∵CE是⊙O的切线，

∴∠OEC＝90°.

∵四边形OABC是平行四边形，

∴OC∥AB，

∴∠EOC＝∠A，∠COD＝∠ODA.

∵OD＝OA，∴∠A＝∠ODA，∴∠EOC＝∠DOC.

在△EOC和△DOC中， ∵

∴△EOC≌△DOC(SAS)，

∴∠ODC＝∠OEC＝90°，

∴OD⊥CD，∴CD是⊙O的切线.

(2)【解】过点D作DF⊥OC于点F.

在Rt△CDO中，OC＝AB＝4，OD＝OA＝BC＝3，

由勾股定理，得CD＝＝＝.

∵S△CDO＝CD·OD＝OC·DF，

∴DF＝＝＝，

∴S平行四边形OABC＝OC·DF＝4×＝3.

【归纳总结】(学生总结，老师点评)有关圆的考查中，切线的判定与性质经常综合运用，在此类问题中，要注意分清是运用判定定理还是性质定理，不能混淆.有时还常常运用判定定理得到切线，再运用性质定理求解，注意解答的逻辑性.

课堂小结

1.切线的判定定理：经过圆的半径的外端且垂直于这条半径的直线是圆的切线.

应用格式：

2.切线的性质定理：圆的切线垂直于经过切点的半径.

应用格式：∵直线l是⊙O 的切线，A是切点，

∴直线l ⊥OA.

布置作业

教材52页练习第1－4题.

板书设计

27.2与圆有关的位置关系

3　切线

第1课时　切线的判定与性质

1.切线的判定定理：经过圆的半径的外端且垂直于这条半径的直线是圆的切线.

2.切线的性质定理：圆的切线垂直于经过切点的半径.

3.常用的辅助线方法.

4.技巧：①连半径，证垂直；②作垂直，证半径.