




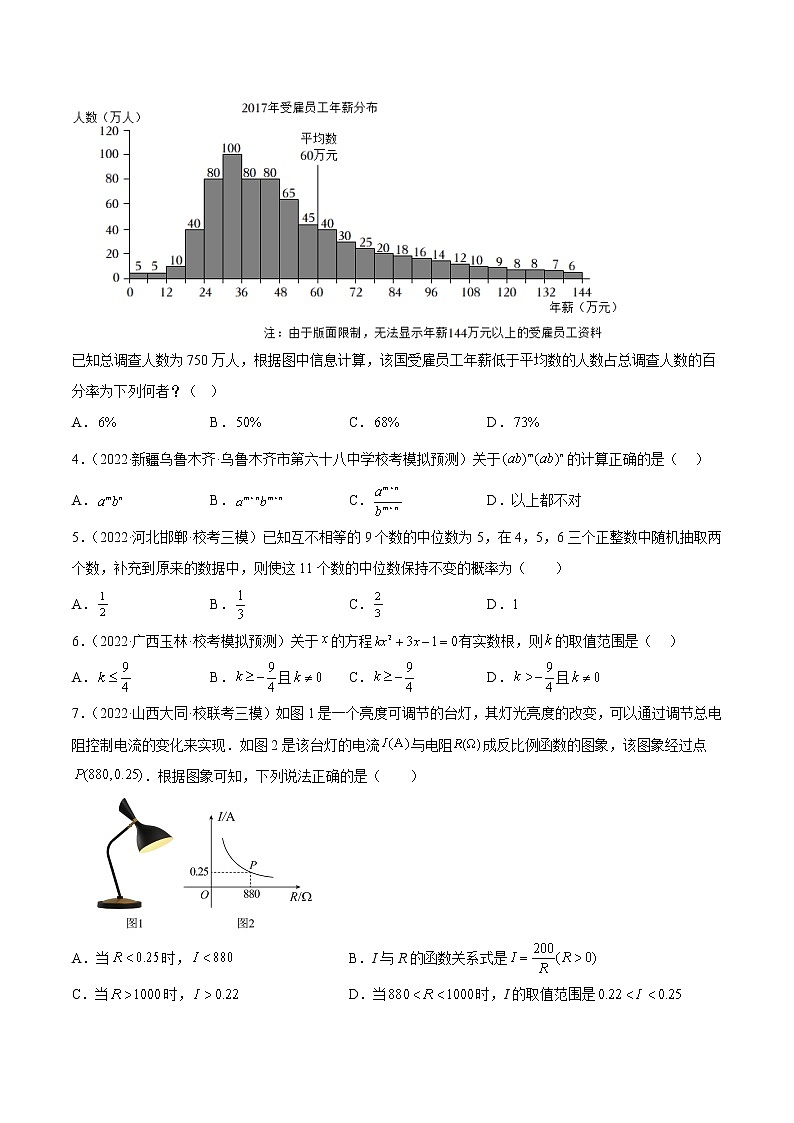


所属成套资源:2022-2023学年九年级数学下学期开学摸底考试卷
数学-2022-2023学年九年级下学期开学摸底考试卷(浙江温州专用)
展开
这是一份数学-2022-2023学年九年级下学期开学摸底考试卷(浙江温州专用),文件包含数学-2022-2023学年九年级下学期开学摸底考试卷浙江温州专用解析版docx、数学-2022-2023学年九年级下学期开学摸底考试卷浙江温州专用参考答案docx、数学-2022-2023学年九年级下学期开学摸底考试卷浙江温州专用考试版docx、数学-2022-2023学年九年级下学期开学摸底考试卷浙江温州专用答题卡docx等4份试卷配套教学资源,其中试卷共48页, 欢迎下载使用。
2022-2023学年九年级下学期开学摸底考试卷(浙江温州专用) 数学 参考答案12345678910CDCBDCDCBD11、 12、 套餐一 13、 且 14、 15、 16、 17.【答案】【分析】首先解不等式,然后根据解集为求解即可.【详解】解:由①得,由②得,∵不等式组的解集为,∴,即k的取值范围为.【点睛】本题考查了解一元一次不等式组,熟练掌握运算法则是解答本题的关键.18.【答案】(1)图见详解(2)图见详解,点旋转到所经过的路径长为【分析】(1)根据轴对称的性质可直接进行作图;(2)由题意先作出图,然后根据弧长公式可求解.【详解】(1)解:线段如图所示:(2)解:线段如图所示,∴,,∴点旋转到所经过的路径长为.【点睛】本题主要考查轴对称图形的性质、旋转的性质、勾股定理与网格问题及弧长计算公式,熟练掌握轴对称图形的性质、旋转的性质、勾股定理与网格问题及弧长计算公式是解题的关键.19.【答案】(1) (2)(3)(4)252人 【分析】(1)由统计表中或先算出抽样人数,再根据频数分布直方图得到的频数,根据频数的和是总数算出,利用“频率等于频数除以总数”计算出频率;(2)利用中位数的定义求出这组数据的中位数;(3)利用“扇形的度数该组的频率”计算出组的圆心角;(4)先计算出样本中成绩大于等于分以上的频率,再计算该校发奖人数.【详解】(1)解:,由频数分布图知,的频数为,所以的频率为..故答案为:,.(2)按得分从小到多排列,第十个数和第十一个数在组,第十个数是,第十一个数是.所以随机抽取的名学生成绩的中位数为.故答案为:.(3)组的频数为,其频率为,组所在扇形圆心角的度数是:.故答案为:.(4)样本中超过分的频率为:,所以该学校这次表彰的人数是:人.【点睛】本题考查了频数分布直方图、中位数等知识点,掌握“各频数的和总数”、“各频率的和”、“扇形角的度数该组的频率”及中位数的定义是解决本题的关键.20.【答案】(1)见解析(2)5【分析】对于(1),分别以A、B两点为圆心,以大于长度为半径画弧,在两边分别相交于两点,然后过这两点作直线,即为的垂直平分线;对于(2),根据线段垂直平分线的性质得出,再根据周长公式即可得出答案.【详解】(1)作图如图所示:(2)的垂直平分线,.,,的周长是:(cm).故答案为:.【点睛】本题主要考查了尺规作图和线段垂直平分线的性质,解题的关键是掌握“垂直平分线上的点到这条线段两端点的距离相等”.21.【答案】(1)(2)P点坐标 【解析】(1)∵四边形是矩形∴,在中,∵∴,∴,∴把代人得,∴∴反比例函数的解析式为;(2)∵点D是CB中点,∴B(8,3)当x=8时 ∴E(8,)当AEP构成等腰三角形时,只能是PA=EA=P点可位于E点左边或右边当P点位于E点左边时:P的横坐标x=8-=当P点位于E点右边时:P的横坐标为x=8+=故P点坐标【点睛】本题考查待定系数法确定反比例函数表达式、矩形性质在求坐标中的应用,等腰三角形性质,掌握这些才能解出此题.22.【答案】(1)见解析(2) 【分析】(1)根据平行四边形的性质和等边三角形的性质证得,即,进而利用平行四边形的判定即可得证;(2)先求得,进而求得,,过G作于H,利用等腰直角三角形的性质和含角的直角三角形的性质求得、、,进而求得即可得所求面积.【详解】(1)证明:∵四边形是平行四边形,∴, ∴,∵等边和等边,∴,,,∴,∴,∴四边形是平行四边形;(2)解:∵,,∴,又,∴,∴,,∴,过G作于H,在中,,,,∴,中,,,∴,∴,∴,∴的面积为.【点睛】本题考查平行四边形的判定与性质、等边三角形的性质、等腰直角三角形的性质、含角的直角三角形的性质、平行线的判定与性质、三角形的内角和定理等知识,熟练掌握相关的知识的联系与运用,证得是解答 的关键.23.【答案】(1)(2)①M点的坐标为或 ;②M点的坐标为或或 【分析】(1)利用待定系数法去求抛物线解析式;(2)①先求出抛物线的对称轴为,作直线于点D,作于E,根据相似三角形的判定和性质进行如下的分类讨论即可:(1)当时,(2)当时进行求解即可;②先确定进行如下的分类讨论即可:(1)当时,(2)当时,(3)当时进行求解即可.【详解】(1)将点,分别代入得,解得,∴抛物线的解析式为;(2)①抛物线的对称轴为直线,作直线于点D,作于E,∵,∴当,即,∴,如图1,∵,∴,∵,∴,∴,而,∴,此时M点的坐标为,∴当,即,∴,如图2,同理可得,∴,而,∴,此时M点的坐标为,综上所述,M点的坐标为或;②∵,∴,当时,,此时点M的坐标为;当时,点N与点P重合,则,∴,此时M点的坐标为;当时,在中,,∵,∴,即,解得,此时点M的坐标为,综上所述,M点的坐标为或或.【点睛】本题考查了二次函数的综合题,熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式;会灵活应用相似三角形的判定和性质进行几何计算;理解坐标与图形的性质;会利用分类讨论的思想解决数学问题.24.【答案】(1)的最小值为7;(2)的最小值为;(3)的长度存在最小值,最小值为米.【分析】(1)连接交圆O于点P,则的值最小,由矩形的性质及圆的性质可求出答案; (2)作的垂直平分线,如图2.作点B关于直线l的对称点,连接、、,交直线于点,连接,证明为等腰直角三角形,由等腰直角三角形的性质求出的长,则可得出答案; (3)如图3,作点D关于的对称点,连接交于点E,则.当取得最小值时,的值最小.以为边向左作等边,作的外接圆,连接、.由直角三角形的性质求出(米).则可得出答案.【详解】解:(1)如图1,连接交圆O于点P,则的值最小, ∵E为的中点,O为的中点,矩形, ∴,, ∴四边形为矩形, ∴, ∴, ∴. (2)作的垂直平分线l,如图2. ∵, ∴点P到的距离等于, ∴点P在内的直线l上. 作点B关于直线l的对称点,连接、、,交直线l于点,连接, 则,,, ∴. ∵, ∴当点P在点的位置时,取得最小值,最小值为的长. ∵,,, ∴. ∴为等腰直角三角形, ∴, 即的最小值为. (3)如图3,作点D关于的对称点,连接交于点E,则. ∴, ∴当点、E、共线时,取得最小值, ∴当取得最小值时,的值最小. 以为边向左作等边,作的外接圆,连接、、∵,, ∴点P在劣弧上运动,连接交于点,则. ∵,, ∴, 即的最小值为的长. ∵为等边的外接圆, ∴平分 , ∴. 又∵, ∴. ∵(米),,, ∴(米),过作于,则,∴(米), ∵为的中点,,∴(米),∴(米), ∴(米). 即的长度存在最小值,最小值为米.【点睛】本题是圆的综合题,考查了三角形的外接圆,垂径定理的应用,等腰三角形的性质,三角形三边关系,直角三角形的性质,等边三角形的性质,矩形的性质与判定,锐角三角函数的应用,本题难度大,正确作出辅助线是解题的关键.
相关试卷
这是一份【开学摸底考】九年级数学(浙江专用)02-2023-2024学年九年级数学下学期开学摸底考试卷.zip,文件包含九年级数学开学摸底考浙江专用02解析版docx、九年级数学开学摸底考浙江专用02答案及评分标准docx、九年级数学开学摸底考浙江专用02考试版docx、九年级数学开学摸底考浙江专用02答题卡docx等4份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。
这是一份【开学摸底考】九年级数学(浙江专用)01-2023-2024学年九年级数学下学期开学摸底考试卷.zip,文件包含九年级数学开学摸底考浙江专用01解析版docx、九年级数学开学摸底考浙江专用01答案及评分标准docx、九年级数学开学摸底考浙江专用01考试版docx、九年级数学开学摸底考浙江专用01答题卡docx等4份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
这是一份数学-2022-2023学年八年级下学期开学摸底考试卷(浙江温州专用),文件包含数学-2022-2023学年八年级下学期开学摸底考试卷浙江温州专用解析版docx、数学-2022-2023学年八年级下学期开学摸底考试卷浙江温州专用参考答案docx、数学-2022-2023学年八年级下学期开学摸底考试卷浙江温州专用考试版docx、数学-2022-2023学年八年级下学期开学摸底考试卷浙江温州专用答题卡docx等4份试卷配套教学资源,其中试卷共51页, 欢迎下载使用。









