专题06 线段最值问题（1）—将军饮马问题-备战中考数学二轮专题归纳提升

专题06 线段最值问题（1）——将军饮马问题

【问题引入】

“白日登山望烽火，黄昏饮马傍交河”，这是唐代诗人李颀《古从军行》里的一句诗。而由此却引申出一系列非常有趣的数学问题，通常称为“将军饮马”。

【模型概述】

求“PA+PB”最值问题，其中P的运动轨迹是一条直线.

【解题思路】

关于最小值，我们知道“两点之间，线段最短”、“点到直线的连线中，垂线段最短”等，所以此处，需转化问题，将折线段变为直线段．作端点（点A或点B）关于折点（上图P点）所在直线的对称，化折线段为直线段．

【题型一——将军饮马问题】

常见的题型有：

问题1. 如图，将军在图中点A处，现在他要带马去河边喝水，之后返回军营，问：将军怎么走能

使得路程最短？

作法：如图．作点A关于直线l的对称点A’，连结A'B，与直线，的交点就是点P

【典型例题】

【例1】如图，在矩形ABCD中，AB＝10，AD＝6，动点P满足S△PAB＝S矩形ABCD，则点P到A，B两点距离之和PA+PB的最小值为　　．

【答案】2

【解析】解：设△ABP中AB边上的高是h．

∵S△PAB＝S矩形ABCD，

∴AB•h＝AB•AD，

∴h＝AD＝4，

∴动点P在与AB平行且与AB的距离是2的直线l上，如图，作A关于直线l的对称点E，连接AE，连接BE，则BE的长就是所求的最短距离．

在Rt△ABE中，∵AB＝10，AE＝4+4＝8，∴BE＝＝＝2，

即PA+PB的最小值为2．故答案为：2．

【练1】如图，等边△ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AC边上一点，若AE＝2，当EF＋CF取得最小值时，则∠ECF的度数为多少？

【答案】∠ECF＝30º

【解析】解：过E作EM∥BC，交AD于N，如图所示：

∵AC＝4，AE＝2，∴EC＝2＝AE，∴AM＝BM＝2，∴AM＝AE，

∵AD是BC边上的中线，△ABC是等边三角形，∴AD⊥BC，

∵EM∥BC，∴AD⊥EM，

∵AM＝AE，∴E和M关于AD对称，连接CM交AD于F，连接EF，则此时EF＋CF的值最小，

∵△ABC是等边三角形，∴∠ACB＝60º，AC＝BC，∵AM＝BM，

∴∠ECF＝∠ACB＝30º.

【练2】如图，四边形ABCD中，DA⊥AB，CB⊥AB，AD＝3，AB＝5，BC＝2，P是边AB上的动点，则PC+PD的最小值是　　．

【答案】5

【解析】解：延长CB到C′，使C′B＝CB＝2，连接DC′交AB于P．则DC′就是PC+PD的和的最小值．

∵AD∥BC，∴∠A＝∠PBC′，∠ADP＝∠C′，∴△ADP∽△BC′P，∴AP：BP＝AD：BC′＝3：2，′∴PBAP，

∵AP+BP＝AB＝5，∴AP＝3，BP＝2，

∴PD3，PC′2，

∴DC′＝PD+PC′＝325，∴PC+PD的最小值是5，

故答案为5．

【练3】如图，矩形ABCD中，AB＝4，BC＝6，点P是矩形ABCD内一动点，且，则PC＋PD的最小值为               .

【答案】

【解析】如图，作PM⊥AD于M，作点D关于直线PM的对称点E，连接PE，EC.设AM＝，

∵四边形ABC都是矩形，  AB//CD， AB＝ CD＝4， BC＝AD＝6，

∵S△PAB＝S△PCD

∴×4×x＝××4×（6-x），

∴x＝2，

∴AM＝2，DM＝EM＝4，

在Rt△ECD中，，

∵PM垂直平分线段DE，∴PD＝PE，

∴PC＋PD＝PC＋PE≥EC，∴PD＋PC≥，

∴PD＋PC的最小值为.

【题型二——将军造桥问题】

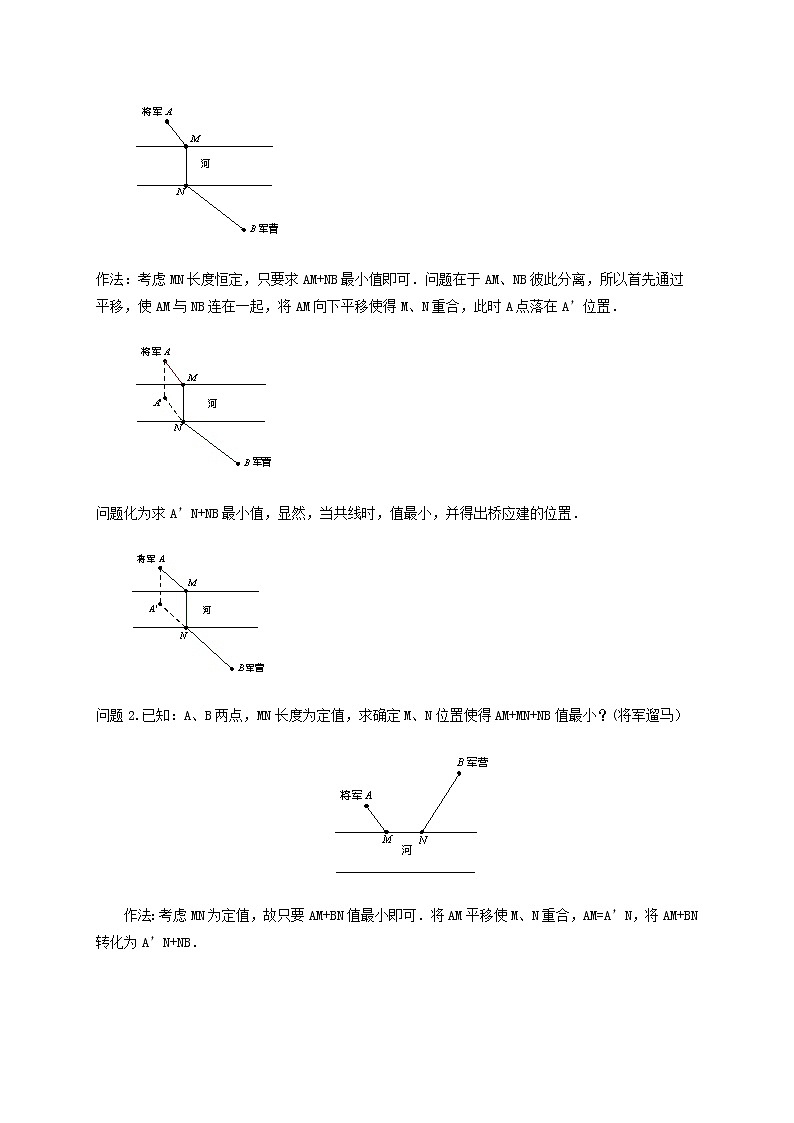
问题1.已知：将军在图中点A处，现要过河去往B点的军营，桥必须垂直于河岸建造，问：桥建在何处能使路程最短？(将军过桥)

作法：考虑MN长度恒定，只要求AM+NB最小值即可．问题在于AM、NB彼此分离，所以首先通过平移，使AM与NB连在一起，将AM向下平移使得M、N重合，此时A点落在A’位置．

问题化为求A’N+NB最小值，显然，当共线时，值最小，并得出桥应建的位置．

问题2.已知：A、B两点，MN长度为定值，求确定M、N位置使得AM+MN+NB值最小？(将军遛马）

作法：考虑MN为定值，故只要AM+BN值最小即可．将AM平移使M、N重合，AM=A’N，将AM+BN转化为A’N+NB．

构造点A关于MN的对称点A’’，连接A’’B，可依次确定N、M位置，可得路线．

【典型例题】

【例1】如图，已知直线l1∥l2，l1、l2之间的距离为8，点P到直线l1的距离为6，点Q到直线l2的距离为4，PQ=，在直线l1上有一动点A，直线l2上有一动点B，满足AB⊥l2，且PA+AB+BQ最小，此时PA+BQ=______．

【答案】16．

【解析】解：作PE⊥l1于E交l2于F，在PF上截取PC=8，连接QC交l2于B，作BA⊥l1于A，

此时PA+AB+BQ最短．作QD⊥PF于D．

在Rt△PQD中，∵∠D=90°，PQ=，PD=18，

∴DQ=，

∵AB=PC=8，AB∥PC，

∴四边形ABCP是平行四边形，

∴PA=BC，CD=10，

∴PA+BQ=CB+BQ=QC==16．

故答案为16．

【练1】（1）如图1，在A和B两地之间有一条河，现要在这条河上建一座桥CD，桥建在何处才能使从A到B的路径最短？（假定河的两岸是平行的直线，桥要与河岸垂直）

（2）如图2，在A和B两地之间有两条河，现要在这两条河上各建一座桥，分别是MN和PQ， 桥分别建在何处才能使从A到B的路径最短？（假定河的两岸是平行的直线，桥要与河岸垂直）

【答案】（1）

（2）

【解析】解：（1）如图，过点B作BB’垂直于河岸，且使BB’长度等于这条河宽，连接AB’交河的一岸于点C，过点C作CD垂直于河岸，与另一岸交点为D，则CD即为架桥最合适的位置．

（2）如图，过点A作AA’垂直于距点A较近的河岸，且使AA’长等于该河宽，同样，过点B作BB’垂直于距点B较近的河岸，且使BB’长等于河宽，连接A’B’分别交两条河相邻的河岸于点N， P， 过点N作NM垂直于该河河岸，与另一岸交点为M， 过P作PQ垂直于该河河岸，与另一岸交点为Q， 则MN， PQ即为架桥最合适的位置．

【练2】如图，矩形ABCD中，AB＝4，BC＝8，E为CD的中点，点P、Q为BC上两个动点，且PQ＝3，当CQ＝   　时，四边形APQE的周长最小．

【答案】

【解析】解：点A向右平移3个单位到M，点E关于BC的对称点F，连接MF，交BC于Q，

此时MQ+EQ最小，

∵PQ＝3，DE＝CE＝2，AE＝＝2，

∴要使四边形APQE的周长最小，只要AP+EQ最小就行，

即AP+EQ＝MQ+EQ，过M作MN⊥BC于N，设CQ＝x，则NQ＝8﹣3﹣x＝5﹣x，

∵△MNQ∽△FCQ，

∴，

∵MN＝AB＝4，CF＝CE＝2，CQ＝x，QN＝5﹣x，

解得：x＝，则CQ＝

故答案为：．

【练3】如图，O为矩形ABCD对角线AC，BD的交点，AB＝9，AD＝18，M，N是直线BC上的动点，且MN＝3，则OM+ON最小值＝　　．

【答案】3

【解析】解：如图所示，作点O关于BC的对称点P，连接PM，将MP沿着MN的方向平移MN长的距离，得到NQ，连接PQ，则四边形MNQP是平行四边形，

∴MN＝PQ＝3，PM＝NQ＝MO，∴OM+ON＝QN+ON，

当O，N，Q在同一直线上时，OM+ON的最小值等于OQ长，

连接PO，交BC于E，

由轴对称的性质，可得BC垂直平分OP，

又∵矩形ABCD中，OB＝OC，∴E是BC的中点，∴OE是△ABC的中位线，∴OEAB＝4.5，

∴OP＝2×4.5＝9，又∵PQ∥MN，∴PQ⊥OP，

∴Rt△OPQ中，OQ3，∴OM+ON的最小值是3，故答案为：3．

【题型三——遛马饮水问题】

问题1.如图，将军在图中的点P处，已知将军需要先带马儿去OM的河边喝水，再去ON的草坪吃草，求最短路径。即：已知：在MON内有一点P，在边ON，OM上分别找点Q，R，使得PQ＋QR＋RP最小．

作法：如图，分别作点P关于射线OM的对称点P'，P"，连结P'P"，与射线ON，OM的交点就是点Q，R．

问题2.已知：在MON内有一点P，在边OM，ON上分别找点R，Q．使得PR＋QR最小

作法：如图，作点P关于射线OM的对称点P'，作P'Q ON，垂足为Q，P'Q与射线ON的交点就是R．

问题3.已知：在MON内有两点P，Q，在边OM，ON上分别找点R，S．使得PR＋RS＋SQ最小．

作法：如图，作点P关于射线OM的对称点P'，作点Q关于射线ON的对称点Q'，连结P'Q'．与射线OM，ON的交点就是R，S．

【典型例题】

【例1】如图，在锐角三角形ABC中，BC＝4，∠ABC＝45º，BD平分∠ABC，M、N分别是BD、BC上的动点，试求CM＋MN的最小值.

【答案】4

【解析】如图所示，过点C作CE⊥AB于点E，交BD于点M'，过点M'作M'N'⊥BC于N'，则CE即为CM＋MN的最小值.

∵BC＝，∠ABC＝45º，BD平分∠ABC，

∴△BCE是等腰直角三角形，

∴

故CM＋MN的最小值为4.

【练1】如图，在四边形ABCD中，DA⊥AB，DA＝6，∠B＋∠C＝150º，CD与BA的延长线交于E点，A刚好是EB中点，P、Q分别是线段CE、BE上的动点，则BP＋PQ最小值是(       )

 A. 12   B. 15   C. 16   D. 18

【答案】D

【解析】解：如图，作点B关于CE的对称点F，连接BF，EF，则EB＝EF，

∵∠B＋∠C＝150º，

∴∠BEC＝30º，

∴∠BEF＝60º，

∴△BEF是等边三角形，

连接BP，PF，PQ，则BP＝FP，则BP＋QP＝FP＋PQ，

当F，P，Q在同一直线上且FQ⊥EB时，BP＋PQ的最小值为FQ的长，此时，Q为EB的中点，故与A重合，

∵DA⊥AB.DA＝6，∴AE ＝，

∴Rt△QEF中，FQ＝AE＝18，

∴BP＋PQ最小值值为18，

故选D.

【练2】如图，在矩形ABCD中，BC＝10，∠ABD＝30°，若点M、N分别是线段DB、AB上的两个动点，则AM+MN的最小值为　　．

【答案】15

【解析】解：作点A关于BD的对称点A′，连接MA′，BA′，过点A′作A′H⊥AB于H．

∵BA＝BA′，∠ABD＝∠DBA′＝30°，

∴∠ABA′＝60°，

∴△ABA′是等边三角形，

∵四边形ABCD是矩形，

∴AD＝BC＝10，

在Rt△ABD中，AB10，

∵A′H⊥AB，∴AH＝HB＝5，∴A′HAH＝15，

∵AM+MN＝A′M+MN≥A′H，∴AM+MN≥15，

∴AM+MN的最小值为15．

故答案为15．

【练3】如图,点A(a,3)，B(b,1)都在双曲线上,点C,D分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为　    　．

【答案】

【解析】解：分别把A(a,3)，B(b,1)代入中，得：a=1，b=3，

则点A的坐标为（1，3），点B的坐标为（3，1）

作点A关于y轴的对称点A′，过点B作x轴的对称点B′，连接A′B′，与x轴，y轴分别交于C、D两点，此时四边形ABCD的周长最小

∴点A′(-1,3)，点B′（3，-1）

∴四边形ABCD的周长=AD+DC+CB+BA

=D A′+DC+C B′+AB

= A′B′+AB

=+

=+

=