函数的单调性、奇偶性、对称性、周期性10大题型

这是一份函数的单调性、奇偶性、对称性、周期性10大题型，文件包含函数的单调性奇偶性对称性周期性10大题型解析版docx、函数的单调性奇偶性对称性周期性10大题型解析版pdf、函数的单调性奇偶性对称性周期性10大题型原卷版docx、函数的单调性奇偶性对称性周期性10大题型学生版pdf等4份试卷配套教学资源，其中试卷共96页， 欢迎下载使用。
函数的单调性、奇偶性、对称性、周期性10大题型
命题趋势
函数的性质是函数学习中非常重要的内容，对于选择题和填空题部分，重点考查基本初等函数的单调性，利用性质判断函数单调性及求最值、解不等式、求参数范围等，难度较小，属于基础题；对于解答题部分，一般与导数结合，考查难度较大。

满分技巧
一、单调性定义的等价形式:
1、函数在区间上是增函数:
任取，且，都有；
任取，且，；
任取，且，；
任取，且，.
2、函数在区间上是减函数:
任取，且，都有；
任取，且，；
任取，且，；
任取，且，.
二、判断函数奇偶性的常用方法
1、定义法：若函数的定义域不是关于原点对称，则立即可判断该函数既不是奇函数也不是偶函数；若函数的定义域是关于原点对称的，再判断与之一是否相等.
2、验证法：在判断与的关系时，只需验证=0及是否成立.
3、图象法：奇（偶）函数等价于它的图象关于原点（轴）对称.
4、性质法：两个奇函数的和仍为奇函数；两个偶函数的和仍为偶函数；两个奇函数的积是偶函数；两个偶函数的积是偶函数；一个奇函数与一个偶函数的积是奇函数.
5、分段函数奇偶性的判断
判断分段函数的奇偶性时，通常利用定义法判断.分段函数不是几个函数，而是一个函数.因此其判断方法也是先考查函数的定义域是否关于原点对称，然后判断与的关系.首先要特别注意与的范围，然后将它代入相应段的函数表达式中，与对应不同的表达式，而它们的结果按奇偶函数的定义进行比较.
三、常见奇、偶函数的类型
1、（）为偶函数；
2、（）为奇函数；
3、（）为奇函数；
4、（）为奇函数；
5、（）为奇函数；
6、为偶函数；
7、为奇函数；
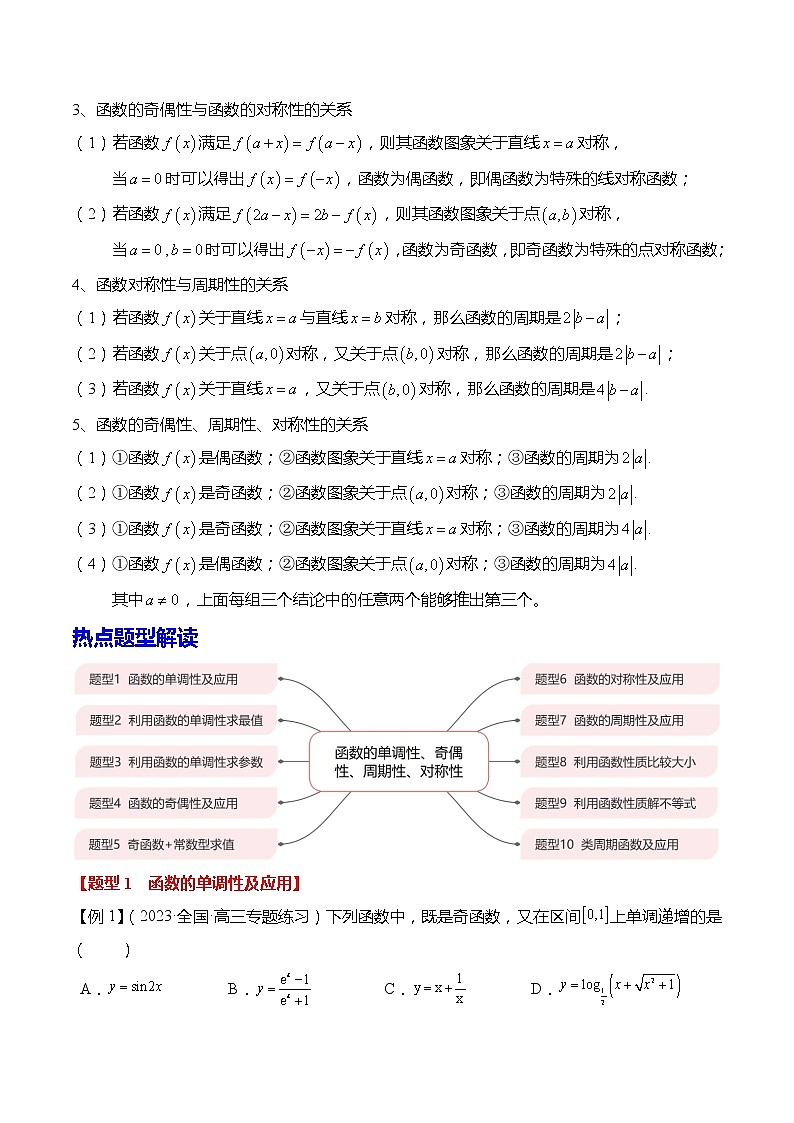
四、函数的周期性与对称性常用结论
1、函数的周期性的常用结论（是不为0的常数）
（1）若，则； （2）若，则；
（3）若，则； （4）若，则；
（5）若，则； （6）若，则（）；
2、函数对称性的常用结论
（1）若，则函数图象关于对称；
（2）若，则函数图象关于对称；
（3）若，则函数图象关于对称；
（4）若，则函数图象关于对称；
3、函数的奇偶性与函数的对称性的关系
（1）若函数满足，则其函数图象关于直线对称，
当时可以得出，函数为偶函数，即偶函数为特殊的线对称函数；
（2）若函数满足，则其函数图象关于点对称，
当,时可以得出，函数为奇函数，即奇函数为特殊的点对称函数；
4、函数对称性与周期性的关系
（1）若函数关于直线与直线对称，那么函数的周期是；
（2）若函数关于点对称，又关于点对称，那么函数的周期是；
（3）若函数关于直线，又关于点对称，那么函数的周期是.
5、函数的奇偶性、周期性、对称性的关系
（1）①函数是偶函数；②函数图象关于直线对称；③函数的周期为.
（2）①函数是奇函数；②函数图象关于点对称；③函数的周期为.
（3）①函数是奇函数；②函数图象关于直线对称；③函数的周期为.
（4）①函数是偶函数；②函数图象关于点对称；③函数的周期为.
其中，上面每组三个结论中的任意两个能够推出第三个。

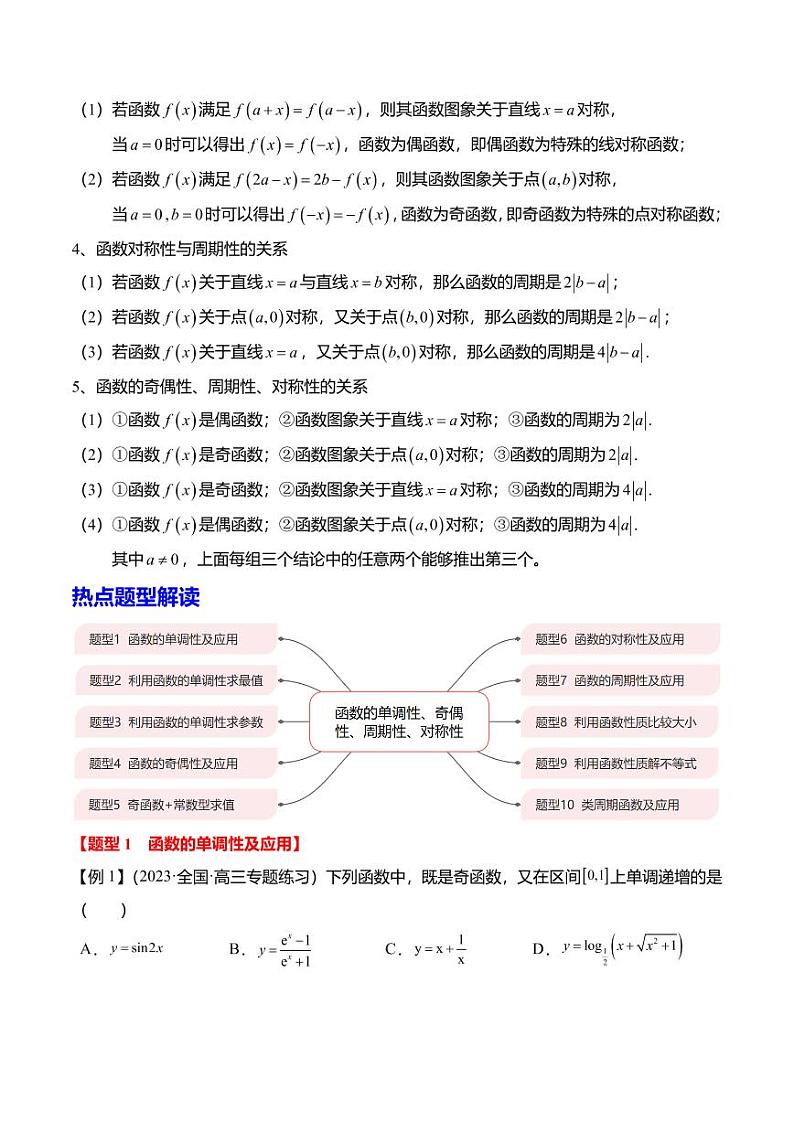
热点题型解读

【题型1 函数的单调性及应用】
【例1】（2023·全国·高三专题练习）下列函数中，既是奇函数，又在区间上单调递增的是（ ）
A． B． C． D．
【答案】B
【解析】时，，而，即，时，取得最大值，
因此在上不是增函数，A错；
，设，则，，
，所以，即，是增函数，
又记，定义域是实数集R，则，
函数为奇函数，B正确；
，但，即在上不是增函数，C错；
设，则，，，
所以，
即函数在上为减函数，D错．故选：B．

【变式1-1】（2022春·北京·高三北京市广渠门中学校考阶段练习）下列函数中，既是奇函数，又在区间上单调递增的是（ ）
A． B． C． D．
【答案】C
【解析】对于A，将代入函数则，故该函数非奇非偶，则A错误；
对于B，将代入函数则，故该函数为奇函数，
任意取，，，
显然该函数在上不是单调递增的，故B错误；
对于C，将代入函数则，故该函数为奇函数，
函数，根据二次函数的性质，
可得该函数在区间上单调递增，故C正确；
对于D，函数的定义域为，则该函数非奇非偶，故D错误.故选：C.

【变式1-2】（2022春·上海崇明·高三上海市崇明中学校考阶段练习）设函数的定义域为．则“在上严格递增”是“在上严格递增”的（ ）条件
A．充分不必要 B．必要不充分 C．充分必要 D．既不充分也不必要
【答案】A
【解析】若函数在上严格递增，对任意的、且，，
由不等式的性质可得，即，
所以，在上严格递增，
所以，“在上严格递增”“在上严格递增”；
若在上严格递增，不妨取，
则函数在上严格递增，但函数在上严格递减，
所以，“在上严格递增”“在上严格递增”.
因此，“在上严格递增”是“在上严格递增”的充分不必要条件.
故选：A.


【变式1-3】（2022春·河北廊坊·高三校考阶段练习）函数的单调递增区间是（ ）
A． B． C． D．
【答案】D
【解析】因为，
所以的增区间为，故选：D.


【变式1-4】（2022春·江苏南通·高三统考开学考试）设函数，，则函数的减区间为（ ）
A． B． C． D．
【答案】B
【解析】依题意，，则得：，
即函数的定义域为，
显然函数在上单调递增，在上单调递减，
而在上单调递减，
因此函数在上单调递减，在上单调递增，
所以函数的减区间为.故选：B


【题型2 利用函数的单调性求最值】
【例2】（2022·河北·校联考模拟预测）已知，则的取值范围为（ ）
A． B． C． D．
【答案】D
【解析】∵
∴原式
令，
则，
当时，，在区间上单调递增，
当时，，在区间上单调递减，
又∵，，，，
∴当时，，
∴当，的取值范围是.故选：D.

【变式2-1】（2022春·安徽安庆·高三安庆一中统考阶段练习）已知函数,则在上的值域为（ ）
A． B． C． D．
【答案】D
【解析】由题知,定义域为,
,
∴在定义域上为偶函数,
则当时,,

，，
,∴在单调递减,
在定义域上为偶函数,∴在单调递增,
∴在单调递增,在单调递减,
,
故在上的值域为.故选:D

【变式2-2】（2022春·海南省直辖县级单位·高三嘉积中学校考阶段练习）已知函数对任意的，总有，若时，，且，则当时，的最大值为（ ）
A．0 B． C．1 D．2
【答案】D
【解析】令，则，得，
令，则，
所以，所以为奇函数，
任取，且，则，，
所以，
所以，所以在上递减，
所以当时，的最大值为，
因为，所以，
所以，故选：D

【变式2-3】（2022春·山东聊城·高三山东聊城一中校考阶段练习）若函数是在R上的奇函数，当时，，则的值域为（ ）
A． B． C． D．
【答案】A
【解析】当时，，
因为是R上的奇函数，所以；
当时，由于图象关于原点对称，故，
所以.故选：A

【变式2-4】（2022·浙江杭州·模拟预测）的最小值是，则实数的取值范围是（ ）
A． B． C． D．
【答案】A
【解析】当时，，令，得，
则在上单调递减，上单调递增，即函数在处取得最小值，
所以问题转化为在上恒成立，
令，则在上恒成立
当时，不符合.
当时，对称轴，则或
解得或，所以，故选：A.


【题型3 利用函数的单调性求参数】
【例3】（2022春·吉林·高三校联考阶段练习）已知函数 (且)是R上的单调函数，则a的取值范围是（ ）
A． B． C． D．
【答案】B
【解析】因为 (且)是R上的单调函数，
若是R上的单调递增函数，则，解得；
若是R上的单调递减函数，则，解得；
综上，a的取值范围是.故选：B.

【变式3-1】（2022春·福建莆田·高三莆田第五中学校考期中）已知函数，满足对任意，都有成立，则a的取值范围是（ ）
A． B． C． D．
【答案】C
【解析】由对任意，都有成立可得，在上单调递减，
所以 ，解得，故选:C.

【变式3-2】（2022春·吉林四平·高三四平市第一高级中学校考阶段练习）已知函数，若对于任意，都有，则的最小值为（ ）
A． B． C． D．0
【答案】B
【解析】因为，所以
可化为，即，
令， 即在单调递增，
当时，在单调递增，
当时，则或，解得或，
综上所述，，即的最小值为.故选：B.

【变式3-3】（2022春·江苏苏州·高三统考阶段练习）已知函数，对任意的，有恒成立，则实数的取值范围为（ ）
A． B． C． D．
【答案】D
【解析】∵对于任意得有，
∴
∴在上单调递增，
∵
∴在上恒成立，
∴，即在上恒成立，，
∵
∴，即实数的取值范围为.故选：D.


【题型4 函数的奇偶性及应用】
【例4】（2022春·北京·高三北京市第十二中学校考阶段练习）下列函数中，既不是奇函数，也不是偶函数的是（ ）．
A． B． C． D．
【答案】D
【解析】由题意，四个函数定义域都是
在中，，是奇函数；
在中，，是偶函数；
在中，，是偶函数；
在中，，
∴既不是奇函数，也不是偶函数；故选：D.

【变式4-1】（2022春·吉林四平·高三四平市第一高级中学校考期末）已知是上的奇函数，且当时，，若，则（ ）
A．-6 B．-7 C．-11 D．-15
【答案】C
【解析】因为是上的奇函数，所以，由得；
即，得，所以；
.故选：C.

【变式4-2】（2022春·陕西西安·高三长安一中校考阶段练习）若是奇函数，则_____，______．
【答案】；
【解析】因为是奇函数，所以其定义域关于原点对称，
由可得，，
所以，解得，
所以函数的定义域为，
因为在处有定义，即，
所以，解得.
【变式4-3】（2022春·福建龙岩·高三福建省连城县第一中学校考阶段练习）函数和的定义域均为，且为偶函数，为奇函数，对，均有，则__________.
【答案】621
【解析】由函数为偶函数，则，
即函数关于直线对称，故；
由函数为奇函数，则，
整理可得，即函数关于对称，故；
由，则，可得，
故，解得，，
.

【变式4-4】（高考真题）定义在上的任意函数都可以表示成一个奇函数和一个偶函数之和，如果，，那么（ ）
A．，
B．，
C．，
D．，
【答案】C
【解析】根据题意，
令则有，
所以，
，故选:C.


【变式4-5】（2023·广西桂林·统考一模）是定义在R上的函数，为奇函数，则（ ）
A．－1 B． C． D．1
【答案】A
【解析】是定义在R上的函数，为奇函数，
则.
∴.故选：A

【题型5 奇函数+常数型求值】
【例5】（2022春·重庆沙坪坝·高三重庆八中校考阶段练习）已知，若，则______.
【答案】8
【解析】设，则.
因为，所以函数的定义域为R，
因为，
所以是一个奇函数.
所以，
又，故.

【变式5-1】（2022春·内蒙古呼和浩特·高三呼市二中校考阶段练习）已知函数，若，则（ ）
A． B． C．3 D．2
【答案】B
【解析】因为，
令，所以，
又因为=
，
所以为奇函数，
因为，即，所以，所以，
所以.故选：B.

【变式5-2】（2023·全国·高三专题练习）已知函数是定义在R上的奇函数，当时，，则函数在R上的解析式为___________．
【答案】
【解析】因为函数是定义在R上的奇函数，则有，
设，有，则，
又由函数为奇函数，则，
则．

【变式5-3】（2022春·吉林·高三校联考阶段练习）已知函数若，则（ ）
A． B．2 C． D．4
【答案】D
【解析】设，则为奇函数，，
因为，所以，所以，
所以.故选:D.

【变式5-4】（2023·全国·高三校联考阶段练习）已知函数，若，则（ ）
A． B． C． D．
【答案】D
【解析】令，则，
为定义在上的奇函数，，
即，.故选：D.

【变式5-5】（2022·上海·高三统考学业考试）已知函数的最大值为M，最小值为m，则M＋m＝（ ）
A．－10 B．10 C．5 D．－5
【答案】A
【解析】设，
则
∴，是奇函数，因此，
又，，
∴，．故选：A．

【题型6 函数的对称性及应用】
【例6】（2022·四川资阳·统考二模）已知函数，则的图象（ ）
A．关于直线对称 B．关于点对称
C．关于直线对称 D．关于原点对称
【答案】A
【解析】对于A项，由已知可得，，
所以的图象关于直线对称，故A项正确；
对于B项，因为，则，故B项错误；
对于C项，，则，故C错误；
对于D项，因为，则，故D错误.故选:A.


【变式6-1】（2022·陕西宝鸡·统考一模）已知函数满足，若函数与的图像恰有四个交点，则这四个交点的横坐标之和为（ ）
A．2 B．4 C．6 D．8
【答案】B
【解析】因为函数满足，
所以，函数图像关于点对称，
因为，
其图像由图像向右平移个单位，再向上平移个单位得到，
所以，函数图像关于点对称，
设数与的图像的四个交点的横坐标为，且，
所以，根据对称性，，
所以，这四个交点的横坐标之和为.故选：B

【变式6-2】（2021春·云南昆明·高三昆明市第三中学校考阶段练习）函数 ，若互不相等，且，则的取值范围是（ ）
A． B． C． D．
【答案】C
【解析】函数的图像如图所示：

设，由函数图像数形结合可知：，
，
．故选：C．

【变式6-3】（2022·上海·统考模拟预测）己知函数满足，若函数与图像的交点为，则________；
【答案】2023
【解析】因为，所以函数关于对称，
又的图像关于对称，
所以两函数的交点也关于对称，
对于每一组对称和，都有，．
从而．

【题型7 函数的周期性及应用】
【例7】（2022春·四川遂宁·高三校考阶段练习）已知是上的奇函数，是上的偶函数，且当时，，则___________．
【答案】
【解析】是上的奇函数
是上的偶函数，，即


又
当时，，，.

【变式7-1】（2022春·山东泰安·高三统考期中）已知函数是定义在R上的偶函数，且对任意实数都有，当时，，则___________.
【答案】
【解析】由于 是偶函数，∴当 时， ；
由 得 ，关于 点对称，
当 时， ， ，
并且函数的周期 ， ， ， ，
∴.

【变式7-2】（2022·全国·模拟预测）若函数的图象关于原点对称，且，则（ ）
A． B．0 C．1 D．2
【答案】A
【解析】由题可知，当时，，且，
由题意知为奇函数，则，
又

，
则.故选：A.

【变式7-3】（2022春·河南·高三期末）已知定义在R上函数，对任意的有，若函数的图像关于直线对称，则=______.
【答案】
【解析】因为函数的图像关于直线对称，
所以函数的图像关于y轴对称，即函数为偶函数，
所以，，，，
所以，函数的周期，，
因为，令，，所以，.
所以

【变式7-4】（2022春·四川·高三四川外国语大学附属外国语学校校考期中）已知是定义在R上的偶函数且，是奇函数，则（ ）
A． B． C． D．
【答案】B
【解析】由于是奇函数，图象关于原点对称，
所以关于对称，所以，
由于是偶函数，所以，
所以，
所以，
所以是周期为的周期函数.
，，
，
所以，
所以.故选：B


【题型8 利用函数的性质比较大小】
【例8】（2021春·江苏淮安·高三江苏省盱眙中学校考期中）已知是偶函数，当时，恒成立，设，，，则a、b、c的大小关系为（ ）
A． B． C． D．
【答案】A
【解析】因为当时，恒成立，
因为，所以，即，
所以在上是增函数，
又因为函数是偶函数，则，
令，得，即，即，
因为，在上是增函数，
所以，即故选：A.

【变式8-1】（2022春·福建莆田·高三校考阶段练习）若函数为偶函数，对任意的 ，且，都有，则（ ）
A． B．
C． D．
【答案】D
【解析】由题意知函数为偶函数，故函数关于直线对称，
由对任意的 ，且，都有，
可知函数在时单调递减，
而，
因为，故，故选：D

【变式8-2】（2022·贵州贵阳·高三贵阳一中校考阶段练习）已知函数为R上的偶函数，对任意不相等的，均有成立，若，则a，b，c的大小关系是（ ）
A． B． C． D．
【答案】D
【解析】∵对任意不等，，均有成立，
∴此时函数在区间上为减函数，
又∵是偶函数，∴当时，为增函数．
由，，
所以，所以，即.故选：D．

【变式8-3】（2022春·山西运城·高三统考期中）已知函数满足：①定义域为，②为偶函数，③为奇函数，④对任意的，且，都有，则的大小关系是（ ）
A． B．
C． D．
【答案】C
【解析】∵ 在R上为偶函数，
∴，∴关于x=1对称.
∵ 在R上为奇函数，∴，
∴关于对称，且
∵，∴（将上式中的x换成x-1）
又∵，∴ ②
∴由①②得： ③
∴由③得： ④ （将③中的x换成x+2）
∴由③④得：
∴的一个周期为，且，关于对称
又∵对任意的，且，都有，
∴在上单调递增.
∴在一个周期内的草图为：

∴，，
∴如图所示：，即：，故选：C.

【题型9 利用函数的性质解不等式】
【例9】（2023·全国·高三专题练习）定义在上的函数满足：对，且，都有成立，且，则不等式的解集为（ ）
A． B． C． D．
【答案】D
【解析】令，
因为对，且，都有成立，
不妨设，则，故，
则，即，
所以在上单调递增，
又因为，所以，故可化为，
所以由的单调性可得，即不等式的解集为.故选：D.

【变式9-1】（2022春·河南驻马店·高三统考阶段练习）定义在上的函数满足：对任意的，有，，则不等式的解集为（ ）
A． B． C． D．
【答案】B
【解析】在上的函数满足：对任意的，有，
所以在上单调递减，
令，则在上单调递减，且，
则由，即，得，
所以不等式的解集为．故选：B．

【变式9-2】（2022春·安徽亳州·高三安徽省亳州市第一中学校考阶段练习）已知函数的定义域为，对定义域内任意，都有，且当时，，则不等式的解集为（ ）
A． B．
C． D．
【答案】A
【解析】由于对定义域内任意，都有，
取 则，
取 则，
则，所以是偶函数，
令，则由时，得
，
所以在上单调递增，
由于，当时，原不等式可化为：，
即，
当时，原不等式可化为：，
即，，
当时，由是偶函数可得或，
故原不等式的解集是：,故选：A

【变式9-3】（2022·辽宁鞍山·鞍山一中校考二模）已知为定义在R上的奇函数，且对任意的非负数，有，且，若，则实数的取值范围是（ ）
A． B． C． D．
【答案】D
【解析】因为对任意的非负数,有
故函数在上为单调递减函数，
又，，所以,即
因为为奇函数，则,所以,解得,
所以实数的取值范围是.故选：D

【变式9-4】（2022·全国·高三专题练习）已知函数，则使不等式成立的x的取值范围是（ ）
A． B． C． D．
【答案】C
【解析】函数定义域为，
显然有，即函数是偶函数，
当时，，令，
，，，
因，则，即，，
有，在上单调递增，
又在上单调递增，因此，在上单调递增，
于是得，解得或，
所以不等式成立的x的取值范围是.故选：C

【题型10 类周期函数及应用】
【例10】（2020春·全国·高三校联考阶段练习）设函数的定义域为，满足，且当时，若对任意，都有，则实数的取值范围是（ ）
A． B． C． D．
【答案】A
【解析】因为对称轴为，所以当时，的最小值为；
当时，，
由知，，
所以此时，其最小值为；
同理，当时，，其最小值为；
当时，的最小值为；
作出如简图，因为，要使，

则有.解得或，
要使对任意，都有，则实数的取值范围是.故选:.

【变式10-1】（2022·高一课时练习）设函数的定义域为R，满足，且当时，．若对任意，都有，则m的取值范围是（ ）
A． B． C． D．
【答案】B
【解析】当时，，则；
当时，，则；
当时，，则，……
由此可得由此作出函数的图象，如图所示．
由图可知当时，令，
整理得，解得或，将这两个值标注在图中．

要使对任意都有，
必有，即实数m的取值范围是.故选：B．

【变式10-2】（2022春·陕西咸阳·高一校考期中）设函数的定义域为，满足，且当时，，若对任意，都有，则的取值范围是（ ）
A． B． C． D．
【答案】C
【解析】,,
当时，在上递减，在上递增，值域为，
当时， ，，值域为，
当时，，，值域为，
当时，，在上递减，在上递增，
且当时，，
令，解得，
即当时，，当时，，
所以当时，对任意都有，
即的取值范围是，故选：C

【变式10-3】（2019春·河南南阳·高三南阳中学校考阶段练习）定义域为R的函数满足，当时，,若时,对任意的都有成立，则实数a的取值范围是（ ）
A． B． C． D．
【答案】D
【解析】当时，

时，
当时，
时，
时，，即对恒成立
即：对恒成立
令，，则
当时，，则在上单调递增
，解得：

【变式10-4】（2022春·吉林长春·高一东北师大附中校考期中）（多选）设函数的定义域为R，满足，且当时，，若对任意，都有，则实数m的取值可以是（ ）
A．3 B．4 C． D．
【答案】ABC
【解析】因为函数的定义域为R，满足，且当时，，
所以当时，，
当时，，
函数部分图象如图所示，

由，得，解得或，
因为对任意，都有，
所以由图可知，故选：ABC


限时检测
（建议用时：60分钟）
1．（2022·河南·统考一模）下列函数中，在定义域内既是奇函数又单调递增的是（ ）
A． B． C． D．
【答案】D
【解析】对于A选项，因为的定义域为，
但，，
故，所以函数不是奇函数，不符合条件，A错误；
对于B选项，函数的定义域为，
，，，
函数在不是增函数，不符合条件，B错误；
对于C选项，函数的定义域为，
，函数为偶函数，不符合条件，C错误；
D选项，因为函数的定义域为，，
所以函数为奇函数，
将函数式变为，因为函数在单调递增，且，
所以函数在单调递增，且，
所以函数在单调递减，且，
所以随着增大，函数的函数值也增大，
即是单调递增函数，符合条件.故选：D.
2．（2023春·广东深圳·高三深圳市高级中学校考期末）已知函数的周期为1，则（ ）
A． B．
C． D．
【答案】A
【解析】因函数的周期为1，
则.
令，则，得的周期为4，则.
，故A正确，C错误.
又由，可得，故B，D错误.故选：A
3．（2022春·甘肃白银·高三校考阶段练习）若偶函数在上是增函数，则（ ）
A． B．
C． D．
【答案】B
【解析】因为在上是增函数，且，所以，
又为偶函数，所以，则，故选：B．
4．（2023·全国·模拟预测）已知是定义域为R的奇函数，满足，则（ ）
A．2 B．1 C． D．0
【答案】D
【解析】因为函数是定义域为R的奇函数，且，
所以，所以，
即函数是周期为的周期函数，
因为函数是定义域为R的奇函数，所以，
因为，所以，
又因为，所以，故选：.
5．（2016·辽宁沈阳·东北育才学校校考一模）已知函数，若在上单调递增，则实数a的取值范围是（ ）
A． B． C． D．
【答案】A
【解析】在上单调递增；
∴，解得；
所以实数a的取值范围为．故选：A．
6．（2023·广西梧州·统考一模）已知定义在R上的函数在上单调递增，若函数为偶函数，且，则不等式的解集为（ ）
A． B． C． D．
【答案】C
【解析】由函数为偶函数，知函数关于对称，
又函数在上单调递增，知函数在上单调递减，
由，知，作出函数的图象，如下：

由图可知，当时，，则；
当时，，则；
当时，，则；
当时，，则；
所以不等式的解集为：或，故选：C
7．（2023春·福建厦门·高三厦门一中校考阶段练习）已知，若，则等于（ ）
A． B． C．0 D．1
【答案】A
【解析】，
，

，，故选：A.
8．（2022春·陕西·高三校联考阶段练习）已知定义在上的函数，对任意两个不相等的实数满足不等式，则实数的最小值为（ ）
A． B． C． D．
【答案】B
【解析】对任意两个不相等的实数，
满足不等式，即，
对任意两个不相等的实数恒成立，
令，则对任意两个不相等的实数，
当时，有，则有在上单调递增，则在上恒成立，
由，所以在上恒成立，
因为，所以问题等价于在上恒成立，
即求解在上的最大值，
由，
当时，，此时在上单调递增，
当时，，此时在上单调递减，
所以，所以，
故实数的最小值为，故选：B.
9．（2022·云南昆明·昆明一中校考模拟预测）（多选）函数分别是定义在上的奇函数和偶函数，且，则（ ）
A． B． C． D．
【答案】AC
【解析】由得：，
又分别是定义在上的奇函数和偶函数，；
由得：，；
对于A，，A正确；
对于B，，B错误；
对于CD，，C正确，D错误.故选：AC.
10．（2021春·广东深圳·高三深圳市龙华中学校考阶段练习）（多选）已知函数，则（ ）
A．在上单调递增 B．在上的最大值为
C．在上单调递减 D．的图像关于直线对称
【答案】BD
【解析】，定义域为，
令，则，
二次函数的图像的对称轴为x=4，
∴的图像关于直线x=4对称，且在(2，4)上递增，在(4，6)上递减,
当x=4时，,故选：BD.
11．（2023春·云南·高三云南师大附中校考阶段练习）（多选）已知定义域为的函数在上单调递增，，且图象关于对称，则（ ）
A．周期 B．在单调递减
C．满足 D．在上可能有1012个零点
【答案】ABD
【解析】A选项：由知的对称轴为，且，
又图象关于对称，即，故，
所以，即，所以，的周期为4，正确；
B选项：因为在上单调递增，，所以在上单调递增，
又图象关于对称，所以在上单调递增，
因为关于对称，所以在上单调递减，，
故在单调递减，B正确；
C选项：根据周期性，，，，
因为关于对称，所以，，
故，错误；
D选项：在上，，有2个零点，
所以在上有1010个零点，在上有2个零点，
故在上可能有1012个零点，正确，故选：ABD．
12．（2022春·江苏南通·高三统考阶段练习）（多选）已知函数及其导函数的定义域均为R，记，，，则（ ）
A． B． C． D．
【答案】ACD
【解析】
令，得，，所以A正确.
令，则
求导数得，，即
所以关于对称，
又因为，所以为偶函数.
，的周期为2.
因为为周期为2的偶函数，所以
令时，
令，得
，所以B不正确，C正确.
因为的周期为2，，所以D正确.故选：ACD.
13．（2022·浙江·模拟预测）已知函数是奇函数，则______.
【答案】-1
【解析】设 ，因为是奇函数，
所以 ，
即 即，
整理得到 ，故得.
14．（2022·河南·统考一模）已知为上的奇函数，当时，，则不等式的解集为___________.
【答案】
【解析】由函数与均在上单调递增，
故在上单调递增，
而为上的奇函数，故在上单调递增，
等价于，得.
15．（2016·辽宁沈阳·东北育才学校校考一模）已知函数在上为增函数．且，．
（1）求的值；
（2）若在函数是单调函数，求m的取值范围．
【答案】（1）；（2）
【解析】（1）由题意，在中
在时成立
∴∴
∵，∴∴∴解得：
（2）由题意及（1）得，
在中，

∵在函数是单调函数
在时，①时，，恒成立．
②时，对于
令 ∵上函数为增函数，
当时，对称轴，∴使成立，∴，∴
当时，使，解得：∴
综上，或
∴m的取值范围为：
16．（2022春·安徽滁州·高三校考阶段练习）已知函数，（其中且）．
（1）判断的奇偶性；
（2）若，判断的单调性；
（3）当的定义域区间为时，的值域为，求的值．
【答案】（1）奇函数；（2）减函数；（3）
【解析】（1）由得或，即的定义域为或，
又
故为奇函数．
（2）由和复合而成，
时，为增函数，
而在和上都为减函数，
由复合函数的单调性知，在和上都为减函数．
（3）由题意，由（2）可知在上为减函数，
故，即，
，又因为，故