冀教版八年级下册22.5 菱形优质课ppt课件

教学目标

1.理解菱形的定义，了解菱形、平行四边形、矩形之间的关系；

2.经历探索菱形性质的过程，掌握菱形的性质；

3.灵活利用菱形的性质解决相关的问题.

教学重难点

重点：探索菱形性质的过程，掌握菱形的性质.

难点：灵活利用菱形的性质解决相关的问题.

教学过程

旧知回顾

1.回忆平行四边形的性质：

边：平行四边形的对边平行且相等.

对角线：平行四边形的对角线互相平分.

角：平行四边形的对角相等，邻角互补.

2.回忆矩形的性质：

除具备平行四边形的一切性质外，另有特性：

①四个角都是直角；②对角线相等；③既是中心对称图形又是轴对称图形.

导入新课                           

感受生活

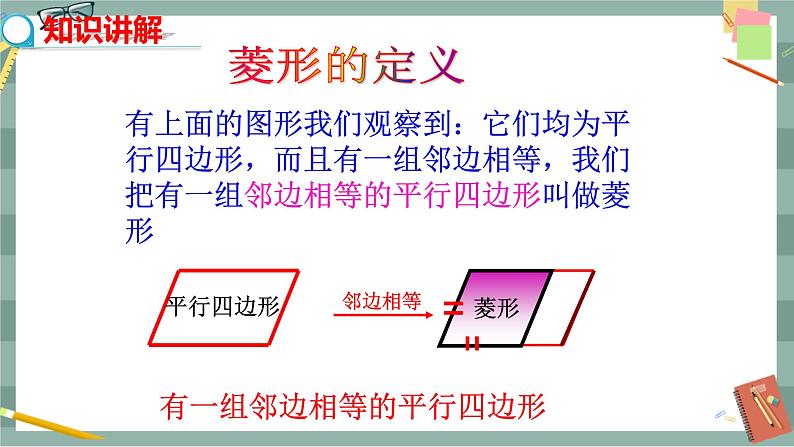
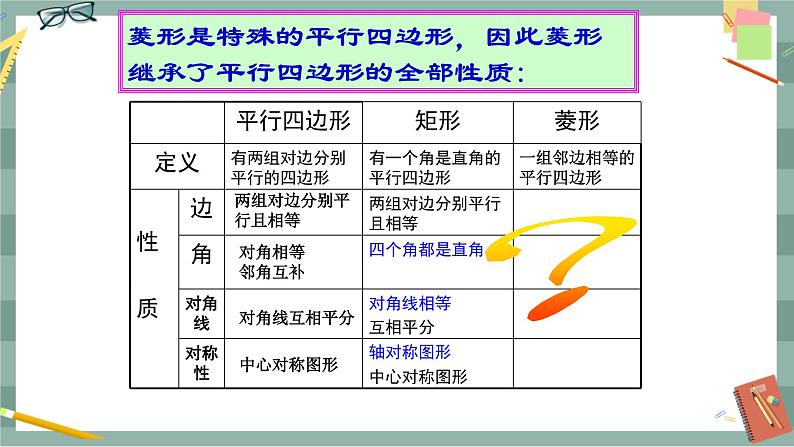
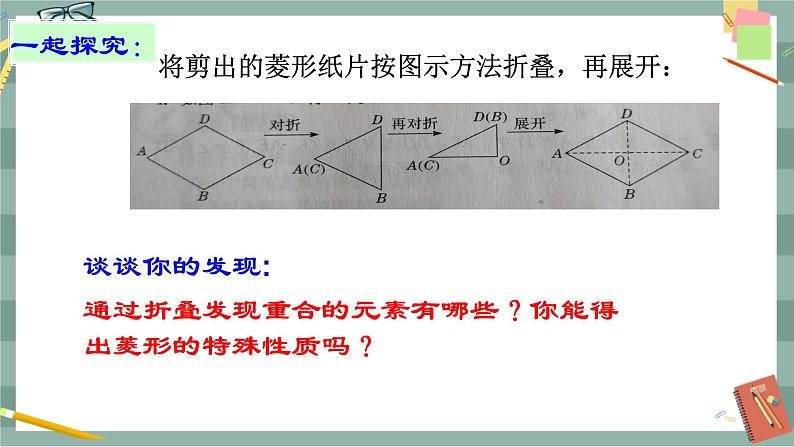
观察这些图形，它们有什么共同特点？与平行四边形有哪些不同？

今天我们来学习菱形的有关性质，教师板书课题.

探究新知 

一、菱形的定义

由上面的图形我们观察到：它们均为平行四边形，而且有一组邻边相等，我们把有一组邻边相等的平行四边形叫做菱形.

因为菱形是特殊的平行四边形，所以菱形继承了平行四边形的全部性质，上一节我们学习了矩形，它也是一个特殊的平行四边形，因此有不同于平行四边形的特殊性质，那么菱形有哪些特殊的性质呢？

二、菱形的性质定理

（一）一起研究

将剪出的菱形纸片按图示方法折叠，再展开.

谈谈你的发现：通过折叠发现重合的元素有哪些？你能得出菱形的特殊性质吗？

学生小组合作，完成菱形性质的探索.

（1）两条折痕的交点O为菱形的中心.

（2）菱形是轴对称图形吗？如果它是轴对称图形，那么它有几条对称轴？都是哪些直线？

答案：菱形是轴对称图形，它有两条对称轴，分别是两条对角线所在的直线.

（3）菱形的四条边有怎样的数量关系？

答案：菱形的四条边相等.

证明你的结论.

已知：如图，四边形ABCD是菱形，AB＝AD.

求证：AB＝AD＝CD＝BC.

证明：∵ 四边形ABCD是菱形，

      ∴ AB＝CD，AD＝CB.

      又∵ AB＝AD，∴ AB＝AD＝CD＝BC.

（4）菱形ABCD的两条对角线有怎样的位置关系？

答案：菱形的两条对角线互相垂直，并且每条对角线平分一组对角.

请证明你的结论.

已知：如图，四边形ABCD是菱形，AC与BD相交于点O.

求证：AC⊥BD，AC平分∠BAD和∠BCD，BD平分∠ABC和∠ADC.

证明：∵ 四边形ABCD是菱形，∴ AB＝AD＝CB＝CD.

∵ BO＝OD ，∴ AC⊥BD，

∴ AC平分∠BAD和∠BCD.

同理可证BD平分∠ADC和∠ABC.

归纳总结：菱形的性质定理

菱形的性质定理1：菱形的四条边都相等.

菱形的性质定理2：菱形的两条对角线互相垂直，且每条对角线平分一组对角.

（二）例题讲解

例1　如图，菱形ABCD的周长为16，∠ABC＝120° ，求对角线BD和AC的长.

解：∵ 菱形ABCD的周长为16， 

∴ AB＝BC＝CD＝AD＝16÷4＝4.

∵ BD平分∠ABC，∴ ∠ABD＝ 60°，

∴ △ABD是等边三角形，∴ BD＝AB＝4.

在Rt△AOB中，OB＝2，AB＝4，

∴ AO＝＝＝＝，∴ AC＝2AO＝.

三、菱形的面积公式

菱形是特殊的平行四边形，那么能否利用平行四边形的面积公式计算菱形的面积?

能.如图，S菱形ABCD＝BC×AE.

思考：利用对角线能计算菱形的面积吗?

教师指点：从对角线互相垂直去考虑.

S菱形ABCD＝S△ABD+S△BCD＝AC×BD.

即菱形的面积＝底×高＝对角线乘积的一半.

例2　如图，菱形花坛ABCD的边长为20 m，∠ABC＝60°，沿着菱形的对角线修建了两条小路AC和BD．求两条小路的长（结果保留小数点后两位）和花坛的面积（结果保留小数点后一位）.

解：∵ 花坛ABCD是菱形，

∴ AC⊥BD，

∠ABO＝∠CBO＝∠ABC＝×60°＝30°，

∴ 在Rt△OAB中，AO＝AB＝×20＝10（m），   

BO＝（m），

∴ 花坛的两条小路长AC＝2AO＝20.0（m），

     BD＝2BO＝≈34.64（m）.

花坛的面积S菱形ABCD ＝AC×BD＝×20×34. 64 ≈346.4（m2）.

四、随堂训练

1.如图1，若要使ABCD成为菱形，则需要添加的条件是（　C　）

A. AB＝CD   　　B. AD＝AC　　　C. AB＝BC  　 D. AC＝BD

2.如图2，O是菱形ABCD的对角线AC，BD的交点，E，F分别是OA，OC的中点，下列结论：

①S△ADE＝S△EOD；

②四边形BFDE是中心对称图形；

③△DEF是轴对称图形；

④∠ADE＝∠EDO.

其中正确的有（　C　）

A.1个 　　　  B.2个 　　　  C.3个 　　　  D.4个

图 1              图2          图3             图4

3.如图3，菱形ABCD的周长是4 cm，∠ABC＝60°，那么这个菱形的对角线AC的长是（　A　）

A.1 cm 　　　  B.2 cm 　　 　 C.3 cm 　　　  D.4 cm

4.如图4，在菱形ABCD中，作BE⊥AD于点E，作CF⊥AB交AB的延长线于点F.

（1）求证：AE＝BF.

（2）若点E恰好是AD的中点，AB＝2，求BD的长.

（1）证明：∵ 四边形ABCD是菱形，

∴ AB＝BC，AD∥BC，

∴ ∠A＝∠CBF.

∵ BE⊥AD，CF⊥AB，

∴ ∠AEB＝∠BFC＝90°.

∴ △AEB≌△BFC（AAS），

∴ AE＝BF.

（2）解：∵ E是AD的中点，且BE⊥AD，

∴ BD＝AB＝2.

课堂小结

1.定义：有一组邻边相等的平行四边形是菱形.

2.菱形的性质定理1：菱形的四条边都相等.

3.菱形的性质定理2：菱形的两条对角线互相垂直，且每条对角线平分一组对角.

布置作业

完成教材第143页习题A组，B组.

板书设计

第二十二章　四边形

22.5　菱　形

第1课时　菱形的性质