初中数学人教版八年级下册17.1 勾股定理获奖ppt课件

这是一份初中数学人教版八年级下册17.1 勾股定理获奖ppt课件，文件包含171勾股定理第2课时勾股定理在实际生活中的应用pptx、RJ中学数学八年级下第十七章171勾股定理第2课时教学详案docx等2份课件配套教学资源，其中PPT共21页， 欢迎下载使用。
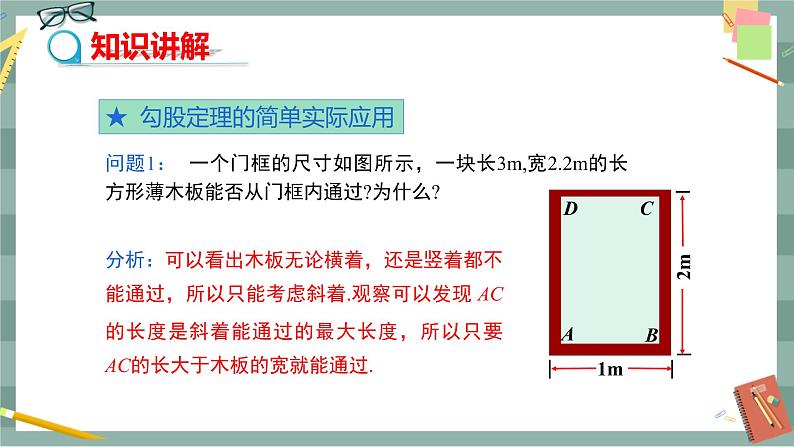
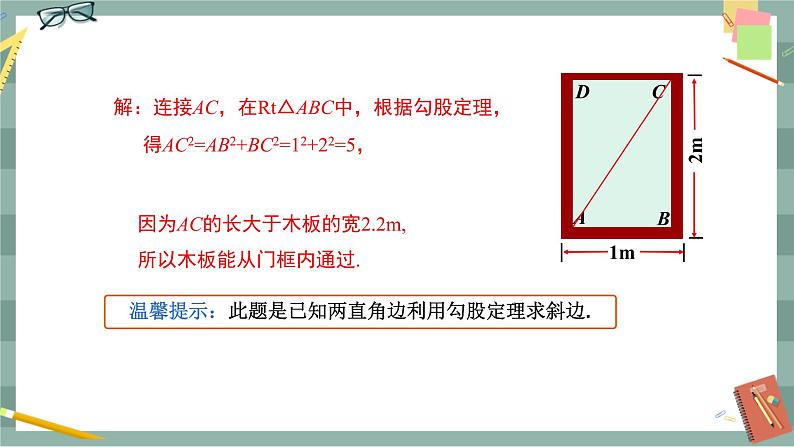
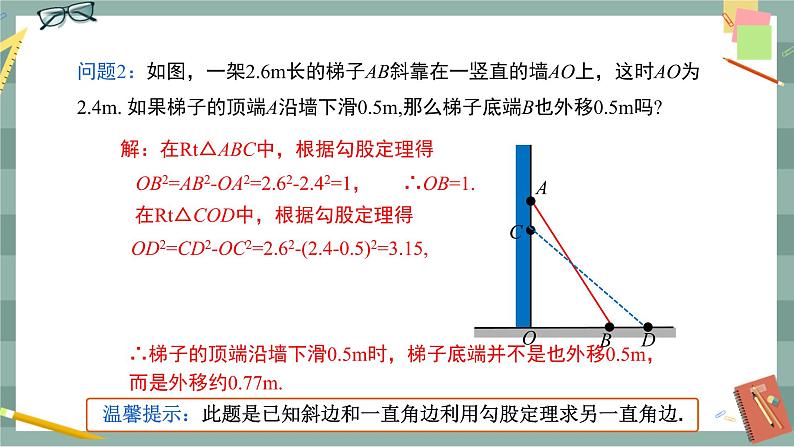
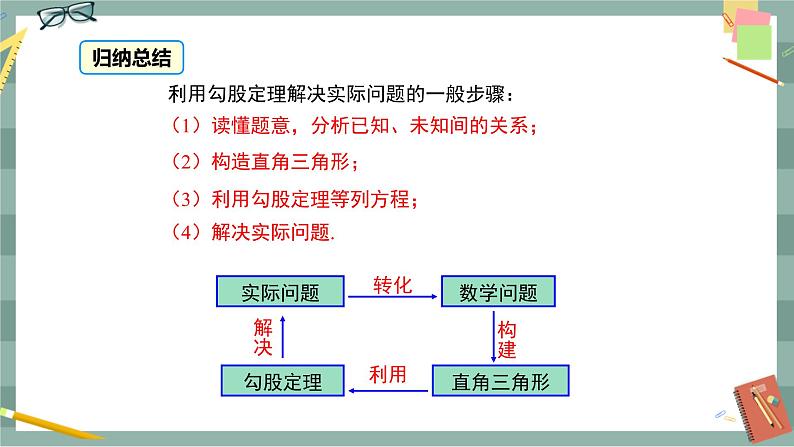
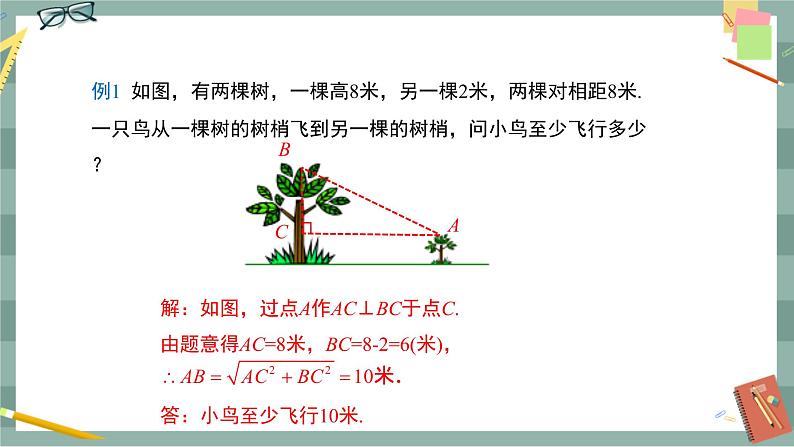
第十七章　勾股定理17.1　勾股定理（第2课时）教学目标1.能利用勾股定理模型解决现实中的问题.2.在勾股定理的应用过程中，发展合情推理能力，感受勾股定理的应用.3.在利用勾股定理解决实际问题的过程中，体验解决问题方法的多样性，培养学生的应用意识.教学重难点重点：勾股定理的应用.难点：勾股定理的应用.教学过程导入新课导入1：回顾（1）复述勾股定理的内容（2）运用勾股定理时，每个直角三角形需知道几个条件？哪几个条件？勾股定理在实际的生产生活中有着广泛的应用.勾股定理的发现和使用解决了许多生活中的问题，今天我们就来运用勾股定理解决一些问题，你可以吗？试一试.导入2：电视的尺寸是屏幕对角线的长度.小华的爸爸买了一台29英寸（74 cm）的电视机，小华量电视机的屏幕后，发现屏幕只有58 cm长和46 cm宽.他觉得一定是售货员搞错了，你同意他的想法吗？你能解释是为什么吗？引导学生回忆勾股定理的内容，学生再尝试解决上面的问题.探究新知教师：勾股定理内容是如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么a2+b2＝c2.可知，如果知道直角三角形的任意两边长就能求出第三边长.例1　一个门框的尺寸如图1所示，一块长3 m，宽2.2 m的长方形薄木板能否从门框内通过？为什么？图1师生活动：学生独立思考，小组讨论，师生共同分析问题：可以看出，木板横着或竖着都不能从门框内通过，只能试试斜着能否通过.门框对角线AC的长度是斜着能通过的最大长度.求出AC，再与木板的宽比较，就能知道木板能否通过.解：在Rt△ABC中，根据勾股定理，得AC2＝AB2+BC2＝12+22＝5，AC＝≈2.24（m）.因为AC大于木板的宽2.2 m，所以木板能从门框内通过.新知应用例2 如图2，一架2.6 m长的梯子AB斜靠在一竖直的墙AO上，这时AO为2.4 m.如果梯子的顶端A沿墙下滑 0.5 m，那么梯子底端B也外移0.5 m吗？（计算结果保留两位小数）图2师生活动：学生独立思考，小组讨论，师生共同分析问题：解决本题的关键是从实际问题中抽象出如图2所示的三角形AOB和三角形COD，分别利用勾股定理求出OB和OD，BD＝OD-OB.解：在Rt△AOB中，根据勾股定理，得OB2＝AB2-OA2＝2.62-2.42＝1，所以OB＝＝1（m）.在Rt△COD中，根据勾股定理，得OD2＝CD2-OC2＝2.62-（2.4-0.5）2＝3.15，OD＝≈1.77（m），BD＝OD-OB≈1.77-1＝0.77（m）.所以梯子的顶端沿墙下滑0.5 m时，梯子底端并不是也外移0.5 m，而是外移约0.77 m.例3　在△ABC中，AB＝，BC＝1，∠ABC＝45°，以AB为一边作等腰直角三角形ABD，使∠ABD＝90°，连接CD，求线段CD的长.师生活动：教师引导学生分析问题，解决本题的关键是画图.根据已知条件画出图形，然后分小组讨论比较所画图形有几种可能，最后师生共同总结.当问题中没有给出图形或某种位置不确定时，需要分类讨论解答.解：分两种情况讨论.（1）点D与点C在AB同侧如图3所示.过点C作CE⊥BD于点E.∵ ∠ABC＝45°，∠ABD＝90°，∴ ∠CBE＝45°，∴ BE＝CE.在Rt△BCE中，BE2+CE2＝BC2，∴ 2CE2＝12，∴ BE＝CE＝.∵ △ABD为等腰直角三角形，∴ BD＝AB＝，∴ ED＝-＝.在Rt△CED中，CD2＝CE2+ED2＝+，∴ CD＝.　　　　图3　　　　　　　 图4　　（2）点D与点C在AB异侧如图4所示.过点D作DE⊥CB交CB的延长线于点E.∵ ∠ABC＝45°，∠ABD＝90°，∴ ∠DBE＝45°，∴ DE＝EB.在Rt△DEB中，DE2+EB2＝DB2，∴ 2EB2＝（）2，∴ DE＝EB＝2.在Rt△DEC中，CD2＝DE2+EC2＝22+32，∴ CD＝.故CD的长为或.课堂小结通过本节课的学习，你有什么收获？说说看！ 布置作业必做：教材第26页练习第1，2题；选做：如图7，已知在△ABC中，∠C＝60°，AB＝14，AC＝10，求BC的长. 图7 板书设计17.1　勾股定理（第2课时）1.勾股定理：a2+b2＝c22.勾股定理的运用：例1　　 　　例2　　　　　例3