数学八年级下册18.1.2 平行四边形的判定优秀ppt课件

这是一份数学八年级下册18.1.2 平行四边形的判定优秀ppt课件，文件包含1812平行四边形的判定第2课时pptx、RJ中学数学八年级下第十八章1812平行四边形的判定第2课时教学详案docx等2份课件配套教学资源，其中PPT共14页， 欢迎下载使用。
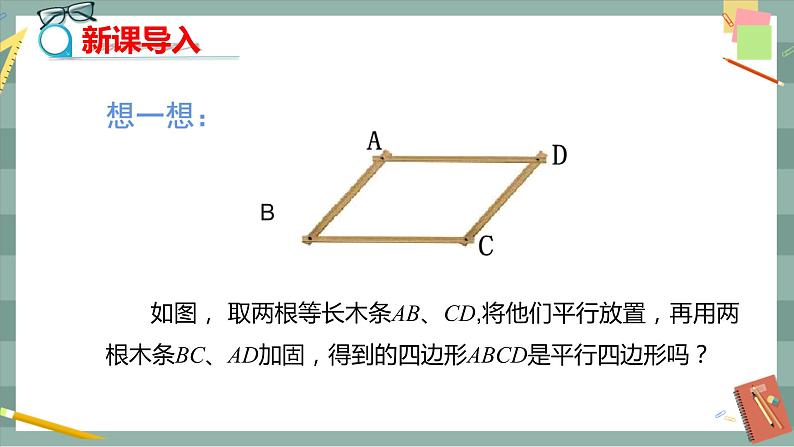
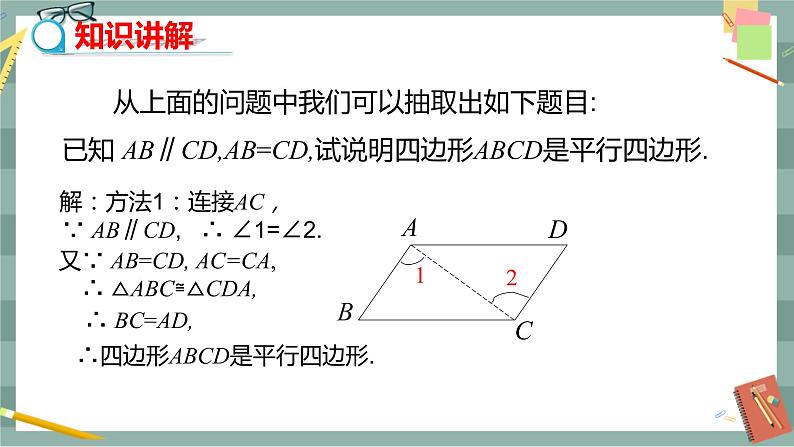
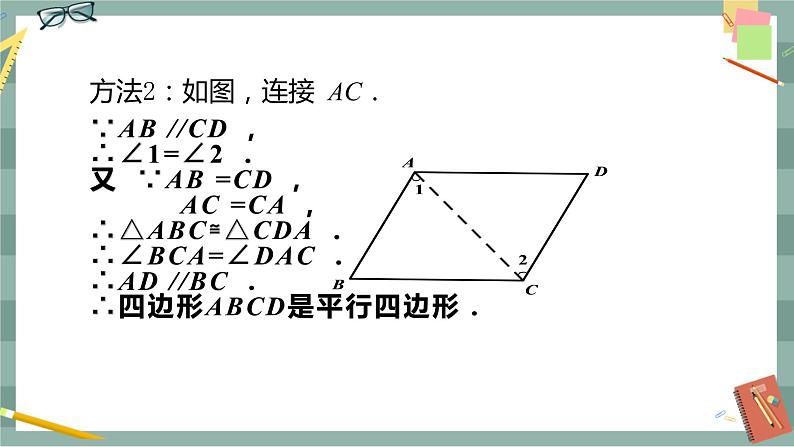
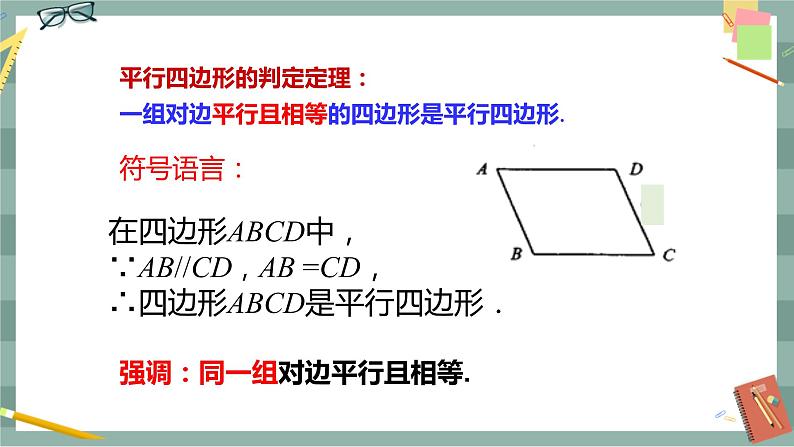
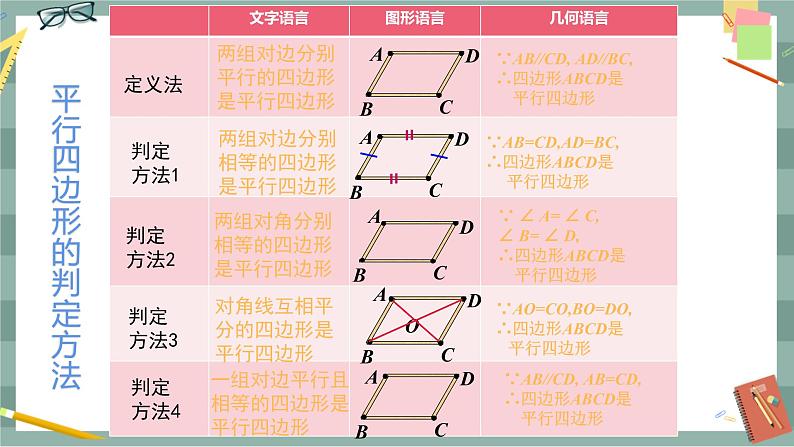
第十八章   平行四边形18.1 平行四边形18.1.2　平行四边形的判定（第2课时）教学目标1.掌握由一组对边平行且相等来判定平行四边形的方法.2.会综合运用平行四边形的判定方法和性质来解决问题.3.通过对平行四边形的性质与判定方法的应用，启迪学生的思维，提高分析问题的能力.教学重难点重点：平行四边形的各种判定方法及其应用，尤其是根据不同条件能正确地选择判定方法.难点：平行四边形的判定定理与性质定理的综合运用.教学过程导入新课1.平行四边形的性质平行四边形的对边相等；平行四边形的对角相等；平行四边形的对角线互相平分.2.我们上节课学习的平行四边形的判定方法有哪些？平行四边形的判定方法1：两组对边分别相等的四边形是平行四边形.平行四边形的判定方法2：两组对角分别相等的四边形是平行四边形.平行四边形的判定方法3：对角线互相平分的四边形是平行四边形.探究新知教师：我们知道两组对边分别平行或相等的四边形是平行四边形.请同学们猜想一下，如果只考虑四边形的一组对边，当它满足什么条件时这个四边形才是平行四边形呢？学生活动：以小组讨论的形式探讨这一问题.问题1：一组对边平行的四边形是平行四边形吗？如果是，请给出证明；如果不是，请举出反例说明. 学生：小学学习过的梯形满足一组对边平行的条件，但梯形不是平行四边形.问题2：满足一组对边相等的四边形是平行四边形吗？学生：如图1所示，这个四边形EFGH满足一组对边EF，HG相等的条件，但它不是平行四边形.　　图1　　　　 　　图2问题3：请你猜想“一组对边平行且相等的四边形是平行四边形”这个命题成立吗？学生活动： 如图2所示，取两根等长的木条AB，CD，将它们平行放置，再用两根木条BC，AD加固，得到的四边形ABCD是平行四边形吗？请你将上述命题改写成已知、求证，并画出图形，然后思考如何证明. 图3已知：如图3所示，在四边形ABCD中，AB∥CD，AB＝CD.求证：四边形ABCD是平行四边形.师生共同分析：要证明四边形ABCD是平行四边形，可证明两组对边分别相等或平行，通过作辅助线，用全等三角形来证明两组对边相等或平行.证明：（方法1）如图3所示，连接AC. ∵ AB∥CD，∴ ∠1＝∠2.∵ AB＝CD，AC＝CA，∴ △ABC≌△CDA（SAS）.∴ BC＝DA.∴ 四边形ABCD是平行四边形.（方法2）如图3所示，连接AC.∵ AB∥CD，∴ ∠1＝∠2.又∵ AB＝CD，AC＝CA，∴ △ABC≌△CDA.∴ ∠BCA＝∠DAC，∴ AD∥BC.∴ 四边形ABCD是平行四边形.师生总结：平行四边形的判定定理：一组对边平行且相等的四边形是平行四边形.几何语言：（如图3所示）在四边形ABCD中，∵ AB∥CD，AB＝CD，∴ 四边形ABCD是平行四边形.图4教师强调：同一组对边平行且相等.新知应用例1　如图4所示，在ABCD中，E，F分别是AD，BC的中点，求证：BE＝DF.分析：证明BE＝DF，可以证明四边形BEDF是平行四边形，也可以证明两个三角形全等，比一比，哪一种方法更简单.证明：（方法1）∵ 四边形ABCD是平行四边形，∴ AD∥BC，AD＝BC.∵ E，F分别是AD，BC的中点，∴ DE∥BF，且DE＝AD，BF＝BC.∴ DE＝BF.∴ 四边形BEDF是平行四边形（一组对边平行且相等的四边形是平行四边形）.∴ BE＝DF.（方法2）∵ 四边形ABCD是平行四边形，∴ AB＝CD，AD＝BC，∠A＝∠C.∵ E，F分别是AD，BC的中点，∴ AE＝AD，CF＝BC，∴ AE＝CF.∴ △ABE≌△CDF.∴ BE＝DF.图5例2　如图5所示，E，F是四边形ABCD的对角线AC上两点，AF＝ CE，DF＝BE，DF∥BE.求证：（1）△AFD≌△CEB；（2）四边形ABCD是平行四边形.分析：（1）利用两边和它们的夹角对应相等的两个三角形全等证明△AFD≌△CEB.（2）（方法1）由△AFD≌△CEB得AD＝BC且AD∥BC，根据“一组对边平行且相等的四边形是平行四边形”证明.（方法2）由△AFD≌△CEB得AD＝BC.由△CDF≌△ABE得AB＝CD.根据“两组对边分别相等的四边形是平行四边形”证明.（方法3）如图6所示，连接DB交AC于点O，连接DE，BF.先证四边形DEBF是平行四边形，得OB＝OD，OE＝OF.由AF＝CE得OA＝OC，根据“对角线互相平分的四边形是平行四边形”证明.证明：（1）∵ DF∥BE，∴ ∠DFE＝∠BEF.又∵ AF＝CE，DF＝BE，∴ △AFD≌△CEB （SAS）.（2）（方法1）由（1）知△AFD≌△CEB，∴ ∠DAC＝∠BCA，AD＝BC，∴ AD∥BC，∴ 四边形ABCD是平行四边形.（方法2）由（1）知△AFD≌△CEB，∴ AD＝BC.∵ DF∥BE，∴ ∠DFE＝∠BEF.又∵ ∠DFE+∠DFC＝180°，∠BEF+∠AEB＝180°，∴ ∠DFC＝∠AEB.∵ AF＝CE，∴ AC-AF＝AC-CE，∴ CF＝AE.在△CDF和△ABE中,∴ △CDF≌△ABE（SAS），∴ AB＝CD.∴ 四边形ABCD是平行四边形.图6（方法3）如图6所示，连接DB交AC于点O，连接DE，BF.∵ DF＝BE，DF∥BE，∴ 四边形DEBF是平行四边形，∴ OD＝OB，OE＝OF.又∵ AF＝CE，∴ AF-OF＝CE-OE，∴ OA＝OC.又∵ OB＝OD，∴ 四边形ABCD是平行四边形.鼓励学生用不同的方法完成，并比较哪种方法简单.课堂小结1.平行四边形的判定方法：一组对边平行且相等的四边形是平行四边形.2.除此以外还有哪些判定方法？用边来判定：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形.用角来判定：两组对角分别相等的四边形是平行四边形.用对角线来判定：两条对角线互相平分的四边形是平行四边形.布置作业教材第50页习题18.1第4题.板书设计18.1.2　平行四边形的判定（第2课时）1.2.用角的关系：两组对角相等3.用对角线的关系：互相平分例1　　　　　例2