2023届高考数学二轮复习专题五概率与统计第3讲统计、成对数据的统计分析课件

这是一份2023届高考数学二轮复习专题五概率与统计第3讲统计、成对数据的统计分析课件，共53页。PPT课件主要包含了热点二独立性检验等内容，欢迎下载使用。

感悟高考 明确备考方向
1.[样本的数字特征] (2022·全国甲卷,T2)某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如图,则(　 　)A.讲座前问卷答题的正确率的中位数小于70%B.讲座后问卷答题的正确率的平均数大于85%C.讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差D.讲座后问卷答题的正确率的极差大于讲座前正确率的极差
2.[频率分布直方图] (2021·全国甲卷,T2)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:根据此频率分布直方图,下面结论中不正确的是(　 　)A.该地农户家庭年收入低于4.5万元的农户比率估计为6%B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%C.估计该地农户家庭年收入的平均值不超过6.5万元D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
解析:对于A,该地农户家庭年收入低于4.5万元的农户比率估计为(0.02+0.04)×1=0.06=6%,故选项A正确;对于B,该地农户家庭年收入不低于10.5万元的农户比率估计为(0.04+0.02×3)×1=0.1=10%,故选项B正确;对于C,估计该地农户家庭年收入的平均值为3×0.02+4×0.04+5×0.10+6×0.14+7×0.20+8×0.20+9×0.10+10×0.10+11×0.04+12×0.02+13×0.02+14×0.02=7.68>6.5万元,故选项C错误;对于D,该地农户家庭年收入介于4.5万元至8.5万元之间的比率为(0.10+0.14+0.20+0.20)×1=0.64>0.5,故估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间,故选项D正确.故选C.
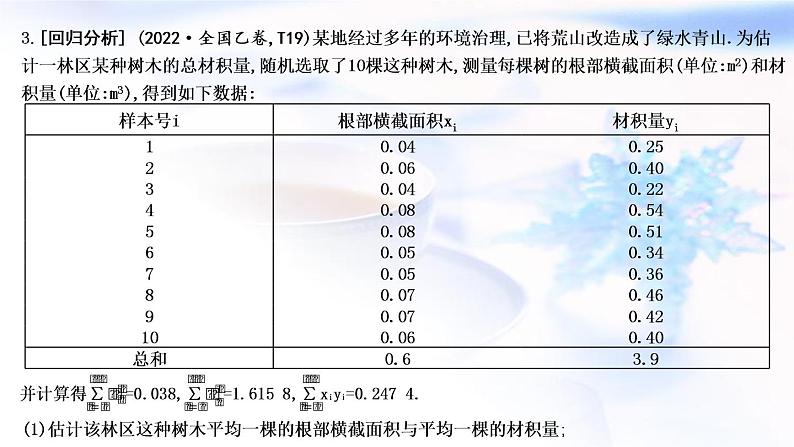
3.[回归分析] (2022·全国乙卷,T19)某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位:m2)和材积量(单位:m3),得到如下数据:
(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量;
(2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到0.01);
(3)现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为186 m2.已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值.
4.[独立性检验] (2022·全国甲卷,T17)甲、乙两城之间的长途客车均由A和B两家公司运营.为了解这两家公司长途客车的运行情况,随机调查了甲、乙两城之间的500个班次,得到下面列联表:
(1)根据上表,分别估计这两家公司甲、乙两城之间的长途客车准点的概率;
(2)能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关?
统计知识主要考查:抽样方法、样本数字特征、统计图表等.以选择题、填空题形式命题,难度较小;回归分析与独立性检验常与概率交汇命题,也是近年的热点,常出现在第19或20题的位置,以中档题为主.此类题目重在考查考生的数学抽象、逻辑推理、数学建模、数学运算、数据分析等核心素养.
突破热点 提升关键能力
热点一　回归分析在实际问题中的应用
2.(1)正相关与负相关就看经验回归直线的斜率,斜率为正则为正相关,斜率为负则为负相关.(2)样本相关系数r具有以下性质:r>0表示两个变量正相关,r<0表示两个变量负相关;|r|≤1,且|r|越接近于1,线性相关程度越强,|r|越接近于0,线性相关程度越弱.
典例1　(2022·四川绵阳三模)随着科技进步,近来年,我国新能源汽车产业迅速发展.以下是中国汽车工业协会2022年2月公布的近六年我国新能源乘用车的年销售量数据:
(1)根据表中数据,求出Y关于x的经验回归方程;(结果保留整数)
(3)你认为(2)中用哪个模型得到的预测值更可靠?请说明理由.
(1)对于非线性回归分析问题,应先进行变量代换,求出代换后的经验回归直线方程,再求经验回归曲线方程.(2)成对样本数据之间线性相关的程度,可以利用样本相关系数判断,|r|越趋近于1,两变量的线性相关程度越强.
热点训练1　 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量Y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到散点图及一些统计量的值.
(2)根据(1)的判断结果及表中数据,建立Y关于x的经验回归方程;
(3)已知这种产品的年利润z与x,Y的关系为z=0.2Y-x,根据(2)的结果回答下列问题:①年宣传费x=49时,年销售量及年利润的预报值是多少?
(3)已知这种产品的年利润z与x,Y的关系为z=0.2Y-x,根据(2)的结果回答下列问题:②年宣传费x为何值时,年利润的预报值最大?
典例2　(2021·山东济南期末)为了研究某种疾病的治愈率,某医院从过往病例中随机抽取了100名患者,其中一部分患者采用了外科疗法,另一部分患者采用了化学疗法,并根据两种治疗方法的治愈情况绘制了等高堆积条形图,如图.(1)根据图表完善以下关于治疗方法和治愈情况的2×2列联表:
解:(1)由题意及等高堆积条形图可得,2×2列联表如表.
典例2　(2021·山东济南期末)为了研究某种疾病的治愈率,某医院从过往病例中随机抽取了100名患者,其中一部分患者采用了外科疗法,另一部分患者采用了化学疗法,并根据两种治疗方法的治愈情况绘制了等高堆积条形图,如图.
独立性检验的具体做法(1)根据实际问题的需要确定容许推断“两个随机事件有关系”犯错误概率的小概率值α,然后查表确定临界值.(2)利用公式,计算χ2.(3)如果χ2>xα,就推断“X与Y有关系”,这种推断犯错误的概率不超过α;否则,就认为在犯错误的概率不超过α的前提下不能推断“X与Y有关系”,或者在样本数据中没有发现足够证据支持结论“X与Y有关系”.
热点训练2　 为进一步做好新冠肺炎疫情防控工作,某社区以网上调查问卷的形式对辖区内部分居民做了新冠疫苗免费接种的宣传和调查.调查数据如下:共95份有效问卷,40名男性中有10名不愿意接种疫苗,55名女性中有5名不愿意接种疫苗.(1)根据所给数据,完成下面的2×2列联表,并根据列联表,根据小概率值α=0.050的χ2独立性检验,判断是否有95%的把握认为是否愿意接种疫苗与性别有关?
热点训练2　 为进一步做好新冠肺炎疫情防控工作,某社区以网上调查问卷的形式对辖区内部分居民做了新冠疫苗免费接种的宣传和调查.调查数据如下:共95份有效问卷,40名男性中有10名不愿意接种疫苗,55名女性中有5名不愿意接种疫苗.(2)从不愿意接种的15份调查问卷中得到拒绝接种新冠疫苗的原因:有3份身体原因不能接种;有2份认为新冠肺炎已得到控制,无需接种;有4份担心疫苗的有效性;有6份担心疫苗的安全性.求从这15份问卷中随机选出2份,在已知至少有一份担心疫苗安全性的条件下,另一份是担心疫苗有效性的概率.
热点三　概率与统计的综合问题
(1)请根据以上数据填写下面2×2列联表,并依据小概率值α=0.001的独立性检验,分析能否认为市民对于交通的满意度与是否为上班族存在关联?
(2)此机构欲随机抽取部分市民进一步调查.规定:抽样的次数不超过n(n∈N*),若随机抽取的市民属于不满意群体,则抽样结束;若随机抽取的市民属于满意群体,则继续抽样,直到抽到不满意市民或抽样次数达到n时,抽样结束.①若n=5,写出X5的分布列和数学期望;
(2)此机构欲随机抽取部分市民进一步调查.规定:抽样的次数不超过n(n∈N*),若随机抽取的市民属于不满意群体,则抽样结束;若随机抽取的市民属于满意群体,则继续抽样,直到抽到不满意市民或抽样次数达到n时,抽样结束.
②请写出Xn的数学期望的表达式(不需证明),根据你的理解说明Xn的数学期望的实际意义.
解决概率与统计综合问题的一般步骤
热点训练3　 (2021·重庆渝中区期末)某中学成功地举办了一年一度的大型学生社团文化节,吸引了众多学生.该中学目前共有社团近40个,由高一和高二学生组成,参加社团的学生有四百人左右.已知该中学高一和高二的所有学生中男生与女生人数比为6∶4,为了解学生参加社团活动的情况,按性别采用分层抽样的方法抽取部分学生,统计得到如图等高堆积条形图.
(1)求该中学参加社团的学生中,任选1人是男生的概率;
(2)若抽取了100名学生,完成下列2×2列联表,并依据小概率值α=0.05的独立性检验,能否认为该中学高一和高二学生的性别与参加学生社团有关联?请说明理由.