2023届高考数学二轮复习专题二平面向量、三角函数与解三角形培优提能三角形中的中线、高线、角平分线问题课件

这是一份2023届高考数学二轮复习专题二平面向量、三角函数与解三角形培优提能三角形中的中线、高线、角平分线问题课件，共23页。PPT课件主要包含了1求角B，1求A的值，1求∠ACB等内容，欢迎下载使用。

[点睛]灵活运用同角的余弦定理,适用于解三角形的题型.
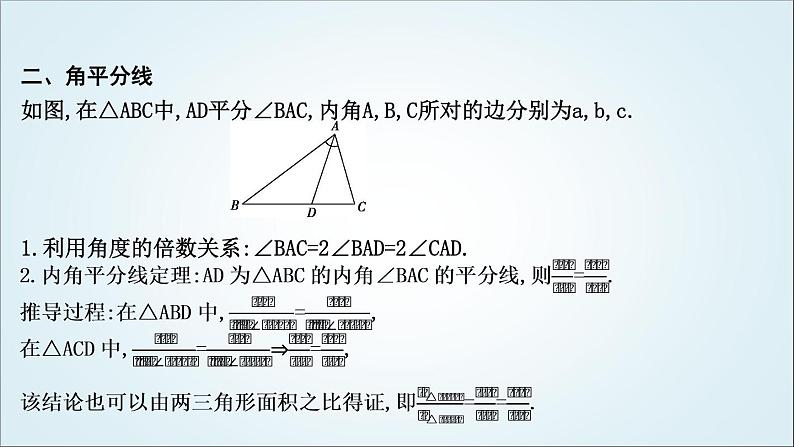
二、角平分线如图,在△ABC中,AD平分∠BAC,内角A,B,C所对的边分别为a,b,c.1.利用角度的倍数关系:∠BAC=2∠BAD=2∠CAD.
2.求高一般采用等面积法,即求某底边上的高,需要求出面积和底边长度.3.高线的两个作用:(1)产生直角三角形;(2)与三角形的面积相关.
培优点1　三角形的中线问题
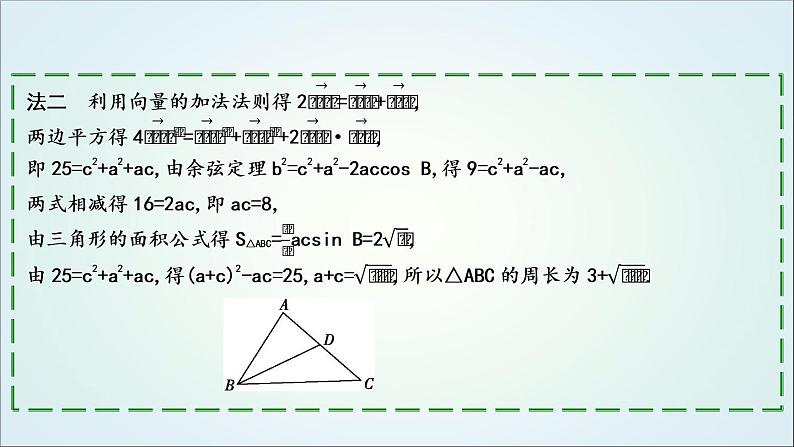
处理与三角形中线有关的问题的常用方法:(1)利用互补角(如本例中∠ADB与∠CDB互补,其余弦值互为相反数)及余弦定理求解.(2)利用中线长定理求解,但要书写其证明过程.(3)利用向量法求解.
培优点2　三角形的角平分线问题
三角形的角平分线性质定理将分对边所成的线段比转化为对应的两边之比,再结合共线定理的推论,就可以转化为向量.一般地,涉及三角形中“定比”类问题,运用向量知识解决起来都较为简捷.
触类旁通2　如图,在△ABC中,内角A,B,C的对边分别为a,b,c.已知b=3,c=6,sin 2C=sin B,且AD为BC边上的中线,AE为∠BAC的平分线.(1)求cs C及线段BC的长;
触类旁通2　如图,在△ABC中,内角A,B,C的对边分别为a,b,c.已知b=3,c=6,sin 2C=sin B,且AD为BC边上的中线,AE为∠BAC的平分线.(2)求△ADE的面积.
培优点3　三角形中的高线问题
典例3　在△ABC中,内角A,B,C的对边分别为a,b,c,且(sin B-sin C)2=sin2A-sin Bsin C.(1)求A;
典例3　在△ABC中,内角A,B,C的对边分别为a,b,c,且(sin B-sin C)2=sin2A-sin Bsin C.
解决与三角形的高线有关的问题常用等积法得到边的关系,进而用正弦定理、余弦定理解决.
(1)求sin B的值;