

2023届高考数学二轮复习专题四立体几何培优提能立体几何中的动态问题学案
展开培优提能 立体几何中的动态问题
立体几何中的“动态问题”是指空间中的某些点、线、面的位置是不确定的或可变的一类开放性问题,解答此类问题应该动静结合、化动为静,找到相应的几何关系,具体有以下几种解决方法:
(1)函数法:某些点、线、面的运动,必然导致某些位置关系或一些变量的变化.变量变化时会引发其他变量的变化,从而建立函数关系,将立体几何问题转化为函数问题来解.
(2)解析法:我们常利用空间直角坐标系解决立体几何问题,即实现几何问题代数化.因此利用空间直角坐标系将空间图形中的若干元素坐标化后,借助向量进行运算和分析,是解决这类问题的常用方法.
(3)等价转换法:动和静是相对的,在运动变化过程中,要善于寻找或构造与之相关的一些不变因素,将一些变化的点、线、面进行合理转换,实现变量与不变量的结合.
培优点1 以静制动(旋转问题、射影问题)
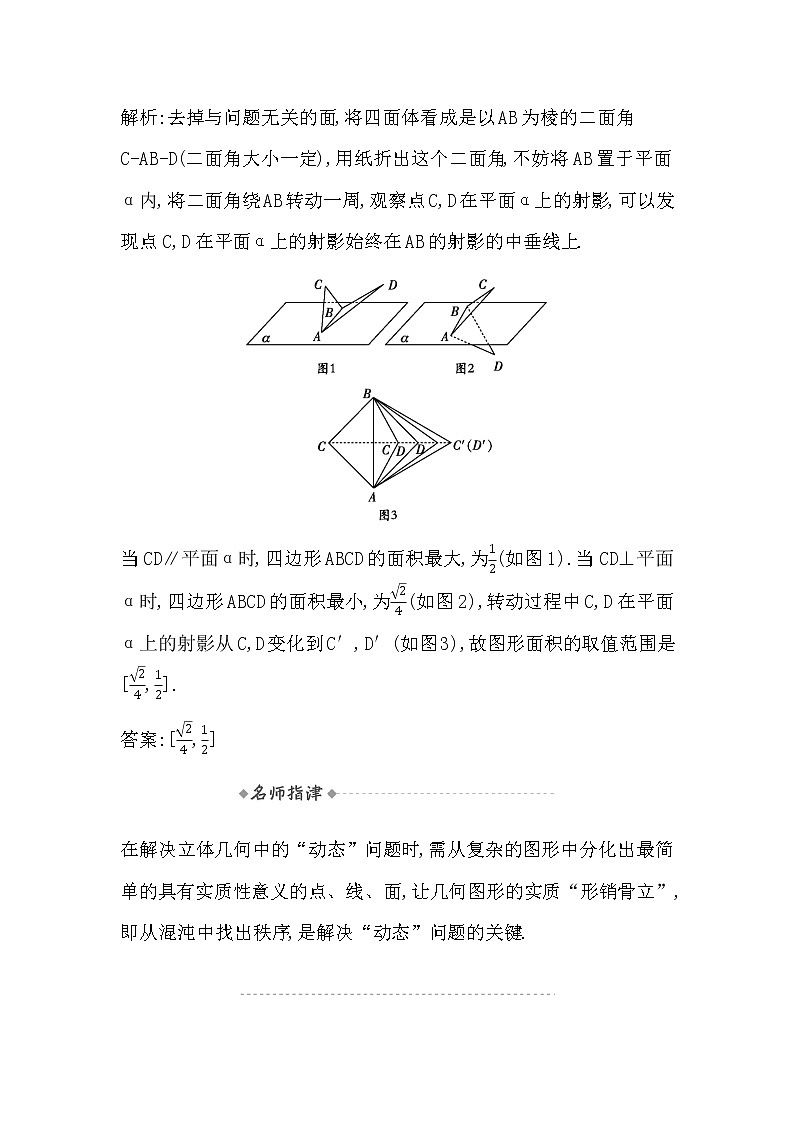
典例1 正四面体ABCD的棱长为1,棱AB∥平面α(如图),则四面体上的所有点在平面α内的射影构成的图形面积的取值范围是 .
解析:去掉与问题无关的面,将四面体看成是以AB为棱的二面角C-AB-D(二面角大小一定),用纸折出这个二面角,不妨将AB置于平面α内,将二面角绕AB转动一周,观察点C,D在平面α上的射影,可以发现点C,D在平面α上的射影始终在AB的射影的中垂线上.
当CD∥平面α时,四边形ABCD的面积最大,为(如图1).当CD⊥平面α时,四边形ABCD的面积最小,为(如图2),转动过程中C,D在平面α上的射影从C,D变化到C′,D′(如图3),故图形面积的取值范围是[,].
答案:[,]
在解决立体几何中的“动态”问题时,需从复杂的图形中分化出最简单的具有实质性意义的点、线、面,让几何图形的实质“形销骨立”,即从混沌中找出秩序,是解决“动态”问题的关键.
触类旁通1 如图,直线l⊥平面α,垂足为O.正方体ABCB1C1D1的棱长为2.点A是直线l上的动点,点B1在平面α内,则点O到线段CD1的中点P的距离的最大值为 .
解析:从题图中分化出4个点O,A,B1,P,其中△AOB1为直角三角形,固定A,B1,点P的轨迹是在与AB1垂直的平面上且以AB1的中点Q为圆心的圆,从而OP≤OQ+QP=AB1+2=+2,
当且仅当OQ⊥AB1,即点O,Q,P共线时,取到等号,此时直线AB1与平面α成45°角.
答案:+2
培优点2 动点轨迹(长度)问题
典例2 在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为棱AB,AD的中点,P为线段C1D上的动点,则直线A1P与平面D1EF的交点Q的轨迹长度为( )
A. B.
C. D.
解析:如图,连接B1D1,
因为E,F分别为棱AB,AD的中点,所以B1D1∥EF,则B1,D1,E,F四点共面.
连接A1C1,A1D,设A1C1∩B1D1=M,A1D∩D1F=N,连接MN,则点Q的轨迹为线段MN,
易得A1D==4,△A1ND1∽△DNF,且=2,所以A1N=A1D=.
易知A1C1=C1D=A1D=4,所以∠C1A1D=60°,
又A1M=2,所以在△A1MN中,由余弦定理可得MN2=A1N2+A1M2-2A1N·A1Mcos 60°=,
所以MN=,即点Q的轨迹长度为.故选C.
空间中动点轨迹问题变化并不多,一般此类问题可以从三个角度进行分析处理,一是从曲线定义或函数关系出发给出合理解释;二是平面与平面交线得直线或线段;三是平面和曲面(圆锥,圆柱侧面,球面)交线得圆、圆锥曲线.很少有题目会脱离这三个方向.
触类旁通2 (多选题)(2022·湖南郴州高三期末)如图,点P是棱长为2的正方体ABCD-A1B1C1D1表面上的一个动点,则( AC )
A.当点P在平面BCC1B1上运动时,四棱锥P-AA1D1D的体积不变
B.当点P在线段AC上运动时,D1P与A1C1所成角的取值范围是[,]
C.当直线AP与平面ABCD所成的角为45°时,点P的轨迹长度为π+4
D.若F是A1B1的中点,当P在底面ABCD上运动,且满足PF∥平面B1CD1时,PF长度的最小值是
解析:当P在平面BCC1B1上运动时,点P到平面AA1D1D的距离不变,正方形AA1D1D的面积不变,故四棱锥P-AA1D1D的体积不变,故A正确;
建立如图所示的空间直角坐标系,
设P(x,2-x,0),0≤x≤2,A1(2,0,2),D1(0,0,2),C1(0,2,2),则=(x,2-x,-2),=(-2,2,0),
设D1P与A1C1所成的角为θ(0≤θ≤),则cos θ=|cos<,>|==,
因为0≤|x-1|≤1,当|x-1|=0时,θ=,
当0<|x-1|≤1时,cos θ==,0<cos θ≤,则≤θ<,
综上,≤θ≤,所以D1P与A1C1所成角的取值范围是[,],故B错误;
因为直线AP与平面ABCD所成的角为45°,
若点P在平面BCC1B1和平面DCC1D1内,因为∠B1AB=45°,∠D1AD=45°已为最大,不成立,
在平面ADD1A1内,点P的轨迹长度是AD1=2,在平面ABB1A1内,点P的轨迹长度是AB1=2,
在平面A1B1C1D1内,如图所示,
作PM⊥平面ABCD,因为∠PAM=45°,所以PM=AM,又PM=AB,所以AM=AB,则A1P=AB,所以点P的轨迹是以A1为圆心,以2为半径的四分之一圆,所以点P的轨迹长度为×2π×2=π,
所以点P的轨迹总长度为π+4,故C正确;
建立如图所示的空间直角坐标系,
设P(x,y,0),x,y∈[0,2],B1(2,2,2),D1(0,0,2),C(0,2,0),F(2,1,2),则=(2,0,2),=(0,-2,2),=(x-2,y-1,-2),
设平面B1CD1的法向量为n=(a,b,c),则即令a=1,则n=(1,-1,-1),
因为PF∥平面B1CD1,所以·n=(x-2)-(y-1)+2=0,即y=x+1,
所以||===≥,
当x=1时,等号成立,故D错误.故选AC.
培优点3 翻折问题
典例3 如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积的最大值为 cm3.
解析:如图,连接OD,交BC于点G,由题意,知OD⊥BC,OG=BC.
设OG=x,则BC=2x,DG=5-x,
三棱锥的高h==,S△ABC=×2x×3x=3x2,
则三棱锥的体积V=S△ABC·h=x2·=·.
令f(x)=25x4-10x5,x∈(0,),则f′(x)=100x3-50x4.令f′(x)=0,得x=2.
当x∈(0,2)时,f′(x)>0,f(x)单调递增;当x∈(2,)时,f′(x)<0,f(x)单调递减.
故当x=2时,f(x)取得最大值80,则V≤×=4.
所以三棱锥体积的最大值为4 cm3.
答案:4
在解决立体几何中的“动态”问题时,对于一些很难把握运动模型(规律)的求值问题,可以通过构建某个变量的函数,以数解形.
触类旁通3 (1)(多选题)(2022·河北唐山高三期末)如图,四边形ABCD是边长为2的正方形,E为AB的中点,将△AED沿DE所在的直线翻折,使A与A′重合,得到四棱锥A′-BCDE,则在翻折的过程中( AB )
A.DE⊥AA′
B.存在某个位置,使得A′E⊥CD
C.存在某个位置,使得A′B∥DE
D.存在某个位置,使四棱锥A′-BCDE的体积为1
(2)(多选题)(2022·广东罗湖高三期末)在△ABC中,AB⊥BC,且AC=2,BC=1,若将△ABC沿AC边上的中线BD折起,使得平面ABD⊥平面BCD.点E在由此得到的四面体ABCD的棱AC上运动,则下列结论正确的为( BCD )
A.∠ADC=
B.四面体ABCD的体积为
C.存在点E使得△BDE的面积为
D.四面体ABCD外接球的表面积为
解析:(1)对于A,如图所示,过A′作A′O⊥DE,垂足为O,延长AO交BC于点F,因为DE⊥AO,
且AO∩A′O=O,AO,A′O⊂平面A′AO,所以DE⊥平面A′AO,又因为A′A⊂平面A′AO,所以DE⊥AA′,A正确;
对于B,取DC的中点G,连接EG,A′G,
当A′在平面ABCD上的射影在直线EG上时,此时DC⊥平面A′EG,从而得到A′E⊥CD,B正确;
对于C,连接A′B,因为点E∈平面A′BE,点D∉平面A′BE,所以直线A′B与DE是异面直线,
所以不存在某个位置,使得A′B∥DE,C错误;
对于D,由=××(1+2)×2×h=1,解得h=1,由A′O⊥DE,
可得A′O===,即此时四棱锥的高h∈(0,],此时<1,
所以不存在某个位置,使四棱锥A′-BCDE的体积为1,D错误.故选AB.
(2)对于A,取BD的中点M,连接CM,因为BC=CD=1,所以CM⊥BD,又平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,
所以CM⊥平面ABD,则CM⊥AD,若∠ADC=,则AD⊥CD,
所以AD⊥平面CBD,则AD⊥BD,显然不可能,A错误;
对于B,易知△BCD的面积为,
在平面ABD中,过A作BD的垂线,交BD的延长线于点H,易知AH=,
因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,所以AH⊥平面BCD,即三棱锥A-BCD的高为AH=,
所以三棱锥A-BCD的体积V=××=,即四面体ABCD的体积为,B正确;
对于C,显然当AC⊥平面BDE时,△BDE的面积取得最小值,
易知CD=1,DH=,由余弦定理可得CH=,所以AC==,
又四面体ABCD的体积为,
所以=×S×,即S=<,
且△BCD的面积为>,
所以存在点E使得△BDE的面积为,C正确;
对于D,设△BCD与△ABD的外心依次为O1,O2,
过O1作平面BCD的垂线l1,过O2作平面ABD的垂线l2,
则四面体ABCD的外接球球心O为直线l1与l2的交点,延长CO1交BD于点M,则M为BD的中点,连接O2M,
则四边形MO1OO2为矩形,结合正弦定理可求得O2M=,O1C=,
所以四面体ABCD的外接球半径为R=OC====,
则四面体ABCD外接球的表面积为S=4πR2=4π×=,D正确.故选BCD.
培优点4 动态最值问题
典例4 (多选题)(2022·江苏常州高三期末)已知正方体ABCD-A1B1C1D1的棱长为3a,点M是棱BC上的定点,且BM=2CM,点P是棱C1D1上的动点,则( )
A.当PC1=a时,△PAM是直角三角形
B.四棱锥A1-PAM体积的最小值为a3
C.存在点P,使得直线BD1⊥平面PAM
D.任意点P,都有直线BB1∥平面PAM
解析:由已知及计算可得PC1=a,AM=a,AP=a,MP=a,
所以AP2=MP2+AM2,所以△PAM为直角三角形,A正确;
=×3a×a=a2,当P与C1重合时,点P到平面AA1M的距离最小,设点P到平面AA1M的距离为h,
在B1C1上取M1,使B1M1=2C1M1,sin ∠B1M1A1==,所以hmin=a,
所以==××h≥×a2× a=a3,B正确;
因为BD1⊥平面AB1C,平面AB1C与平面PAM不平行,所以BD1与平面PAM不垂直,C错误;
P与C1重合时,平面PAM为平面C1AM,BB1∥CC1,
若BB1∥平面PAM,则CC1⊂平面C1AM,与CC1⊄平面C1AM矛盾,D错误.故选AB.
解决与空间图形有关的线段、角、距离、面积、体积等最值问题,一般可以从三方面着手:
(1)从问题的几何特征入手,充分利用其几何性质去解决;
(2)利用空间几何体的侧面展开图;
(3)找出问题中的代数关系,建立目标函数,利用代数方法求目标函数的最值.解题途径很多,在函数建成后,可用一次函数的端点法,二次函数的配方法、公式法,函数有界法(如三角函数等)及导数法等.
触类旁通4 (多选题)(2022·广东揭阳高三期末)如图所示,已知正方体ABCD-A1B1C1D1的棱长为2,M,N分别是AD,CC1的中点,P是线段AB上的动点,则下列说法正确的是( BD )
A.平面PMN截正方体所得的截面可以是四边形、五边形或六边形
B.当点P与A,B两点不重合时,平面PMN截正方体所得的截面是五边形
C.△MPN是锐角三角形
D.△MPN面积的最大值是
解析:如图所示,当点P与A,B两点不重合时,将线段MP向两端延长,分别交CD,CB的延长线于点O,Q,连接NO,NQ分别交DD1,BB1于R,S两点,连接RM,SP,此时截面为五边形MPSNR,故B正确;
当点P与点A或点B重合时,截面为四边形,不可能为六边形,故A错误;
考虑△MPN,当点P与点A重合时,MN=,PM=1,PN=3,
此时因为MN2+PM2<PN2,故∠PMN为钝角,故C错误;
当点P与点B重合时,点P到直线MN的距离取到最大值,△MPN的面积取到最大值,
此时MN=,BM=BN=,则MN边上的高为=,
△MPN的面积为××=,即最大值为,故D正确.故选BD.
高考数学一轮复习第7章8立体几何中的动态问题学案: 这是一份高考数学一轮复习第7章8立体几何中的动态问题学案,共17页。
2024届高考数学一轮复习第6章思维深化微课堂立体几何中的动态问题学案: 这是一份2024届高考数学一轮复习第6章思维深化微课堂立体几何中的动态问题学案,共4页。
高考数学一轮复习第6章思维深化微课堂立体几何中的动态问题学案: 这是一份高考数学一轮复习第6章思维深化微课堂立体几何中的动态问题学案,共4页。












