新高考数学二轮复习专题四第1讲空间几何体课件

这是一份新高考数学二轮复习专题四第1讲空间几何体课件，共60页。PPT课件主要包含了考情分析，空间几何体的折展问题，考点一，核心提炼，规律方法，表面积与体积，考点二，多面体与球，考点三，专题强化练等内容，欢迎下载使用。
空间几何体的结构特征是立体几何的基础，空间几何体的表面积和体积是高考的重点与热点，多以选择题、填空题的形式考查，难度中等或偏上.
空间几何体的侧面展开图1.圆柱的侧面展开图是矩形.2.圆锥的侧面展开图是扇形.3.圆台的侧面展开图是扇环.
(1)“莫言下岭便无难，赚得行人空喜欢.”出自南宋诗人杨万里的作品《过松源晨炊漆公店》.如图是一座山的示意图，山大致呈圆锥形，山脚呈圆形，半径为40 km，山高为40 km，B是山坡SA上一点，且AB＝40 km.为了发展旅游业，要建设一条从A到B的环山观光公路，这条公路从A出发后先上坡，后下坡，当公路长度最短时，下坡路段长为
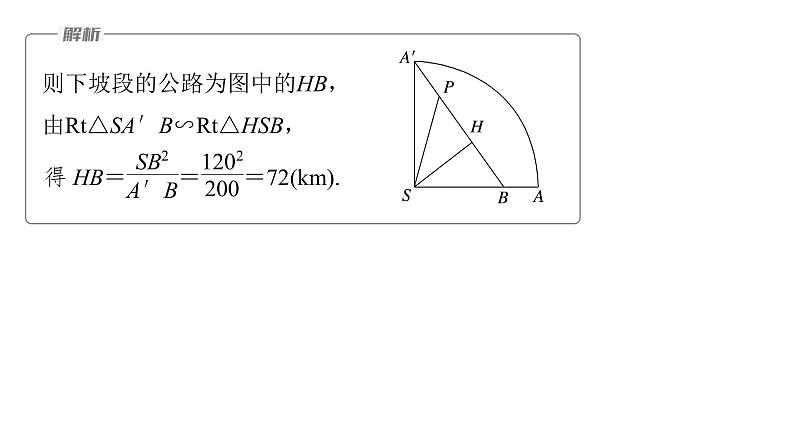
如图，展开圆锥的侧面，连接A′B，
过点S作A′B的垂线，垂足为H，记点P为A′B上任意一点，连接PS，当上坡时，P到山顶S的距离PS越来越小，当下坡时，P到山顶S的距离PS越来越大，
则下坡段的公路为图中的HB，由Rt△SA′B∽Rt△HSB，
由题意知，AE＝AD＝AB＝1，BC＝2，在△ACE中，由余弦定理知，CE2＝AE2＋AC2－2AE·AC·cs∠CAE
∴在△BCF中，由余弦定理知，
空间几何体最短距离问题，一般是将空间几何体展开成平面图形，转化成求平面中两点间的最短距离问题，注意展开后对应的顶点和边.
(1)(多选)如图是一个正方体的展开图，如果将它还原为正方体，则下列说法中正确的是A.C∈GHB.CD与EF是共面直线C.AB∥EFD.GH与EF是异面直线
由图可知，还原正方体后，点C与G重合，即C∈GH，又可知CD与EF是平行直线，即CD与EF是共面直线，AB与EF是相交直线(点B与点F重合)，GH与EF是异面直线，故A，B，D正确，C错误.
(2)如图，在正三棱锥P－ABC中，∠APB＝∠BPC＝∠CPA＝30°，PA＝PB＝PC＝2，一只虫子从A点出发，绕三棱锥的三个侧面爬行一周后，又回到A点，则虫子爬行的最短距离是
将三棱锥由PA展开，如图所示，则∠APA1＝90°，所求最短距离为AA1的长度，∵PA＝2，∴由勾股定理可得
1.旋转体的侧面积和表面积(1)S圆柱侧＝2πrl，S圆柱表＝2πr(r＋l)(r为底面半径，l为母线长).(2)S圆锥侧＝πrl，S圆锥表＝πr(r＋l)(r为底面半径，l为母线长).(3)S球表＝4πR2(R为球的半径).
2.空间几何体的体积公式(1)V柱＝Sh(S为底面面积，h为高).
方法一　因为甲、乙两个圆锥的母线长相等，
不妨设两个圆锥的母线长为l＝3，甲、乙两个圆锥的底面半径分别为r1，r2，高分别为h1，h2，则由题意知，两个圆锥的侧面展开图刚好可以拼成一个周长为6π的圆，所以2πr1＝4π，2πr2＝2π，得r1＝2，r2＝1.
方法二　设两圆锥的母线长为l，甲、乙两圆锥的底面半径分别为r1，r2，高分别为h1，h2，侧面展开图的圆心角分别为n1，n2，
(2)(多选)(2022·新高考全国Ⅱ)如图，四边形ABCD为正方形，ED⊥平面ABCD，FB∥ED，AB＝ED＝2FB.记三棱锥E－ACD，F－ABC，F－ACE的体积分别为V1，V2，V3，则A.V3＝2V2 B.V3＝V1C.V3＝V1＋V2 D.2V3＝3V1
如图，连接BD交AC于O，连接OE，OF.设AB＝ED＝2FB＝2，则AB＝BC＝CD＝AD＝2，FB＝1.因为ED⊥平面ABCD，FB∥ED，所以FB⊥平面ABCD，
因为ED⊥平面ABCD，AC⊂平面ABCD，所以ED⊥AC，又AC⊥BD，且ED∩BD＝D，ED，BD⊂平面BDEF，所以AC⊥平面BDEF.因为OE，OF⊂平面BDEF，所以AC⊥OE，AC⊥OF.
所以EF2＝OE2＋OF2，所以OF⊥OE.又OE∩AC＝O，OE，AC⊂平面ACE，所以OF⊥平面ACE，
所以V3≠2V2，V1≠V3，V3＝V1＋V2,2V3＝3V1，所以选项A，B不正确，选项C，D正确.
空间几何体的表面积与体积的求法(1)公式法：对于规则的几何体直接利用公式进行求解.(2)割补法：把不规则的图形分割成规则的图形，或把不规则的几何体补成规则的几何体，不熟悉的几何体补成熟悉的几何体.(3)等体积法：选择合适的底面来求体积.
由SA与圆锥底面所成角为45°，
(2)(2022·连云港模拟)如图是一个圆台的侧面展开图，若两个半圆的半径分别是1和2，则该圆台的体积是
如图，设上底面的半径为r，下底面的半径为R，高为h，母线长为l，则2πr＝π·1,2πR＝π·2，
下底面面积S＝π·12＝π，
求空间多面体的外接球半径的常用方法(1)补形法：侧面为直角三角形，或正四面体，或对棱均相等的模型，可以还原到正方体或长方体中去求解；(2)定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据到其他顶点距离也是半径，列关系式求解即可.
(1)(2022·烟台模拟)如图，三棱锥V－ABC中，VA⊥底面ABC，∠BAC＝90°，AB＝AC＝VA＝2，则该三棱锥的内切球和外接球的半径之比为
因为VA⊥底面ABC，AB，AC⊂底面ABC，所以VA⊥AB，VA⊥AC，又因为∠BAC＝90°，所以AB⊥AC，而AB＝AC＝VA＝2，所以三条互相垂直且共顶点的棱，可以看成正方体中共顶点的长、宽、高，
设该三棱锥的内切球的半径为r，
因为VA⊥AB，VA⊥AC，AB＝AC＝VA＝2，
由三棱锥的体积公式可得，
设该棱台上、下底面的外接圆的圆心分别为O1，O2，连接O1O2(图略)，则O1O2＝1，其外接球的球心O在直线O1O2上.
所以该球的表面积为4πR2＝100π.综上，该球的表面积为100π.
(1)求锥体的外接球问题的一般方法是补形法，把锥体补成正方体、长方体等求解.(2)求锥体的内切球问题的一般方法是利用等体积法求半径.
(1)(2022·全国乙卷)已知球O的半径为1，四棱锥的顶点为O，底面的四个顶点均在球O的球面上，则当该四棱锥的体积最大时，其高为
该四棱锥的体积最大即以底面截球的圆面和顶点O组成的圆锥体积最大.设圆锥的高为h(0