新高考数学二轮复习专题二微重点8平面向量的最值与范围问题课件

这是一份新高考数学二轮复习专题二微重点8平面向量的最值与范围问题课件，共57页。PPT课件主要包含了求参数的最值范围，考点一，规律方法，考点二，易错提醒，考点三，－22，专题强化练，设Fx0y0，因为－1≤x≤0等内容，欢迎下载使用。

平面向量中的最值与范围问题，是高考的热点与难点问题，主要考查求向量的模、数量积、夹角及向量的系数等的最值、范围.解决这类问题的一般思路是建立求解目标的函数关系，通过函数的值域解决问题，同时，平面向量兼具“数”与“形”的双重身份，数形结合也是解决平面向量中的最值与范围问题的重要方法.
(2)设非零向量a，b的夹角为θ，若|a|＝2|b|，且不等式|2a＋b|≥|a＋λb|对任意θ恒成立，则实数λ的取值范围为A.[－1,3] B.[－1,5]C.[－7,3] D.[5,7]
∵非零向量a，b的夹角为θ，若|a|＝2|b|，a·b＝|a||b|cs θ＝2|b|2cs θ，不等式|2a＋b|≥|a＋λb|对任意θ恒成立，∴(2a＋b)2≥(a＋λb)2，∴4a2＋4a·b＋b2≥a2＋2λa·b＋λ2b2，整理可得(13－λ2)＋(8－4λ)cs θ≥0恒成立，∵cs θ∈[－1,1]，
利用共线向量定理及推论(1)a∥b⇔a＝λb(b≠0).
所以λ＝μ＝0，从而有λ＋μ＝0；
因为M，B，C三点共线，
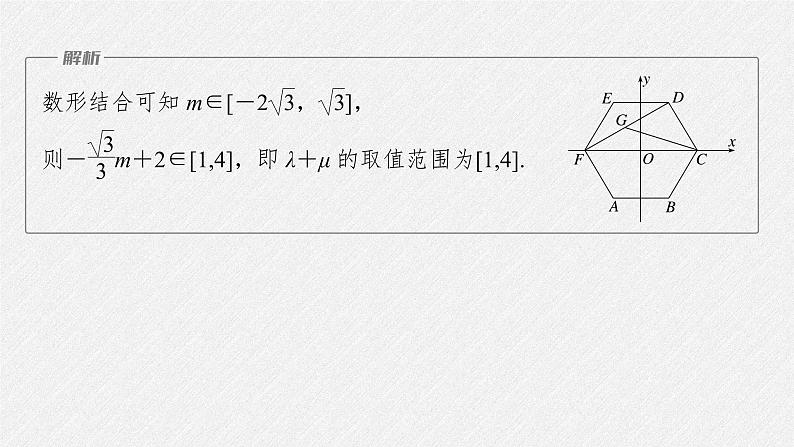
综上，λ＋μ的取值范围是[0,1].
求向量模、夹角的最值(范围)
(1)已知e为单位向量，向量a满足：(a－e)·(a－5e)＝0，则|a＋e|的最大值为A.4 B.5 C.6 D.7
可设e＝(1,0)，a＝(x，y)，则(a－e)·(a－5e)＝(x－1，y)·(x－5，y)＝x2－6x＋5＋y2＝0，即(x－3)2＋y2＝4，则1≤x≤5，－2≤y≤2，
即|a＋e|的最大值为6.
找两向量的夹角时，要注意“共起点”以及向量夹角的取值范围是[0，π]；若向量a，b的夹角为锐角，包括a·b>0和a，b不共线，同理若向量a，b的夹角为钝角，包括a·b<0和a，b不共线.
(2022·马鞍山模拟)已知向量a，b满足|a－3b|＝|a＋3b|，|a＋b|＝4，若向量c＝λa＋μb(λ＋μ＝1，λ，μ∈R)，且a·c＝b·c，则|c|的最大值为A.1 B.2 C.3 D.4
由|a－3b|＝|a＋3b|得a·b＝0，所以a⊥b.如图，
由a⊥b可知OA⊥OB，
即m2＋n2＝16，所以2mn≤16，则mn≤8，当且仅当m＝n时取得等号.
由c＝λa＋μb(λ＋μ＝1)，可知A，B，C三点共线，
由a·c＝b·c可知(a－b)·c＝0，所以OC⊥AB，
所以|c|的最大值为2.
求数量积的最值(范围)
(1)(2022·福州质检)已知平面向量a，b，c均为单位向量，且|a－b|＝1，则(a－b)·(b－c)的最大值为
∵|a－b|2＝a2－2a·b＋b2＝2－2a·b＝1，
∴(a－b)·(b－c)＝a·b－a·c－b2＋b·c
∵cs〈a－b，c〉∈[－1,1]，
因为菱形ABCD的边长为2，∠ABC＝60°，
因为点P在BC边上(包括端点)，所以设P(t，0)，其中t∈[－2,0].
向量数量积最值(范围)问题的解题策略(1)形化：利用平面向量的几何意义将问题转化为平面几何中的最值或范围问题，然后根据平面图形的特征直接进行判断.(2)数化：利用平面向量的坐标运算，把问题转化为代数中的函数最值与值域、不等式的解集、方程有解等问题，然后利用函数、不等式、方程的有关知识来解决.
以点O为原点，AB为x轴，垂直于AB的直线为y轴，建立平面直角坐标系，如图所示，
设P(cs α，sin α)(α∈[0，π])，
因为〈a，b〉＝θ，θ∈[0，π]，
如图，以点B为坐标原点，BC，BA所在直线为x轴、y轴，建立平面直角坐标系，设AB＝a，BP＝x(0≤x≤a)，因为AD＝1，BC＝2，所以P(0，x)，C(2,0)，D(1，a)，
5.(多选)已知向量a，b，单位向量e，若a·e＝1，b·e＝2，a·b＝3，则|a＋b|的可能取值为
设e＝(1,0)，a＝(x1，y1)，b＝(x2，y2)，由a·e＝1得x1＝1，由b·e＝2得x2＝2，由a·b＝x1x2＋y1y2＝3，可得y1y2＝1，
当且仅当y1＝y2＝1时取等号.
如图，以AB的中点O为原点建立平面直角坐标系，则A(－1,0)，D(－1,2)，E(1,1)，连接OP，设∠BOP＝α(α∈[0，π])，则P(cs α，sin α)，
得2μ＝cs α＋1且2λ＋μ＝sin α，α∈[0，π]，
当α＝0时，μmax＝1，故B正确；
方法一　连接AC，BD交于点O，以点O为坐标原点，以BD所在直线为x轴，AC所在直线为y轴，建立如图所示的平面直角坐标系，
连接AC(图略)，因为E为CD的中点，
8.已知向量a，b满足|a|＝1，|b|＝3，则|2a＋b|＋|2a－b|的最小值是____，最大值是_______.