2022年中考数学专题复习课件 探直线与抛物线的交点问题

这是一份2022年中考数学专题复习课件 探直线与抛物线的交点问题，共13页。PPT课件主要包含了问题引入，y-x+b，解析法，图象法，临界点，问题探究1，问题探究2，问题探究3，知识拓展，拓展提升等内容，欢迎下载使用。
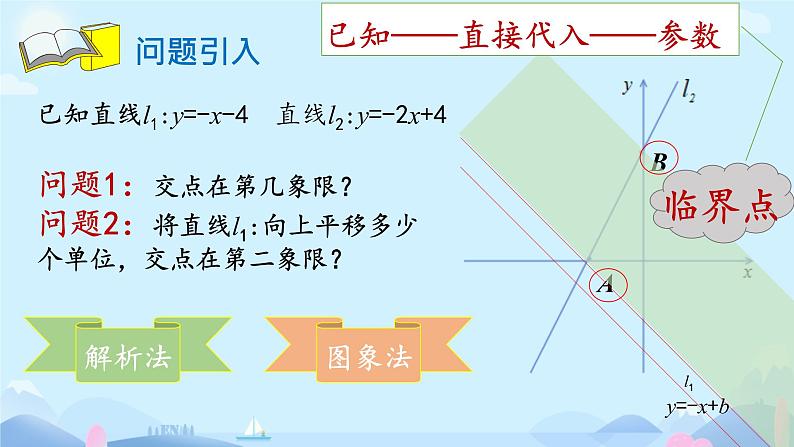
已知直线l1:y=-x-4 直线l2:y=-2x+4问题1：交点在第几象限？ 问题2：将直线l1:向上平移多少 个单位，交点在第二象限？
已知——直接代入——参数
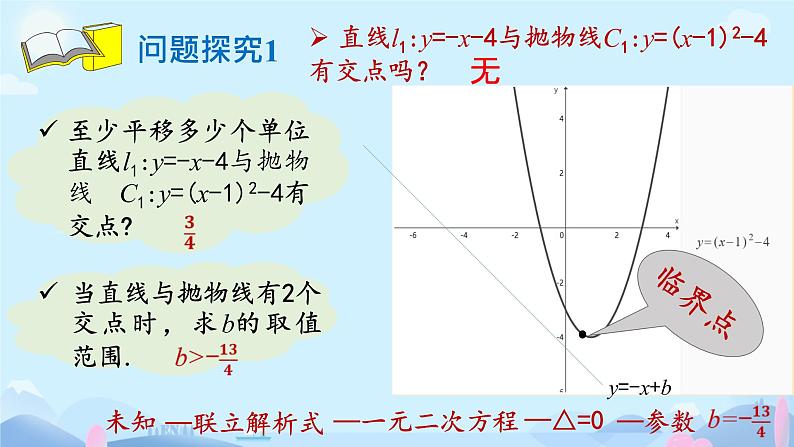
直线l1:y=-x-4与抛物线C1:y=(x-1)2-4有交点吗？
至少平移多少个单位直线l1:y=-x-4与抛物线C1:y=(x-1)2-4有交点?
当直线与抛物线有2个交点时，求b的取值范围.
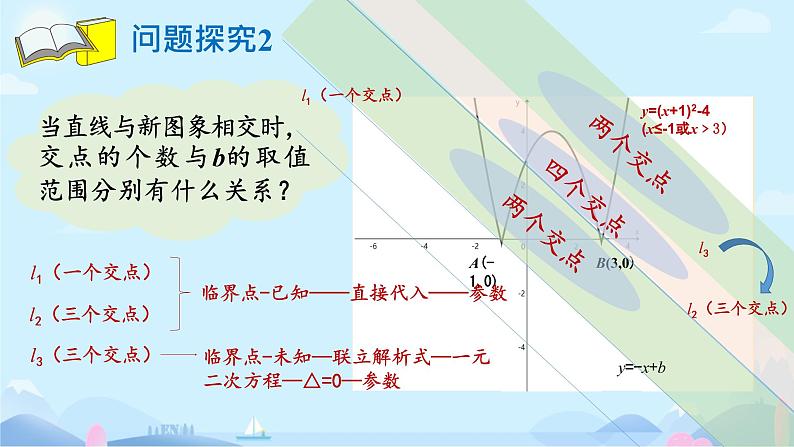
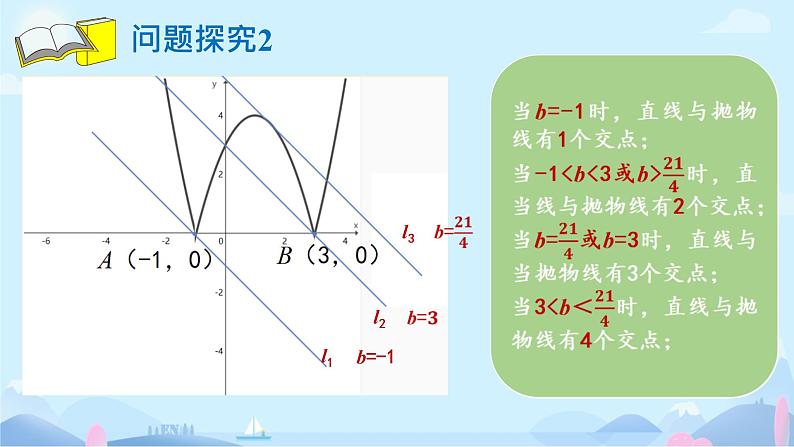
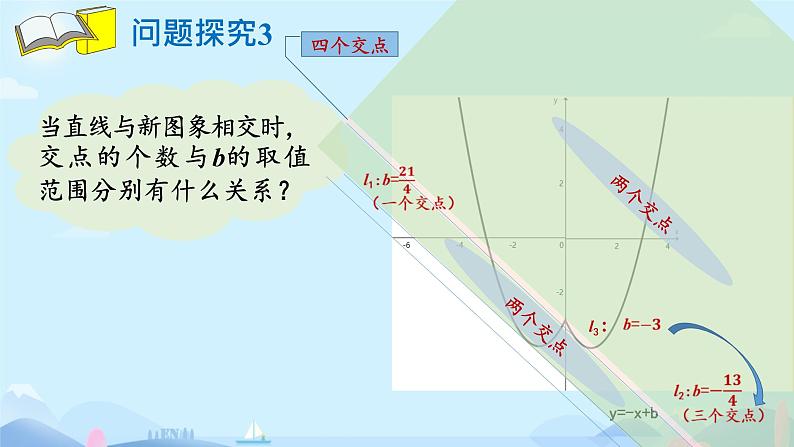
当直线与新图象相交时，交点的个数与b的取值范围分别有什么关系？
y=(x+1)2-4(x≤-1或x﹥3）
临界点-已知——直接代入——参数
临界点-未知—联立解析式—一元二次方程—△=0—参数
y1=(x-2)(x-3)
利用图象，观察直线和抛物线的交点，如果交点是定点，将定点坐标代入相应的解析式，求出参数的值；若交点坐标不确定，则联立解析式，组成方程组，消元得到一元二次方程，用△与0的大小，可求参数的值或范围.