




2023年九年级数学中考复习专题:阿氏圆探究及其应用课件PPT
展开一、模型名称由来【模型背景】“PA+k·PB”型的最值问题是近几年中考考查的热点更是难点。当k值为1时,即可转化为“PA+PB”之和最短问题,就可用我们常见得“饮马问题”模型来处理,即可以转化为轴对称问题来处理。而当k取不为1的正数时,若再以常规的轴对称思想来解决问题,则无法进行,因此必须转换思路。此类问题的处理通常以动点P所在图像的不同来分类,一般为2类研究,即点P在直线上运动和点P在圆上运动。其中点P在直线上运动的类型称之为“胡不归”问题;点P在圆周上运动的类型称之为“阿氏圆”问题。
【模型由来】“阿氏圆”又称“阿波罗尼斯圆”,已知平面上两点A、B,则所有满足PA=k·PB(k≠1)的点的轨迹是一个圆,这个轨迹最早由古希腊数学家阿波罗尼斯发现,故称“阿氏圆”。
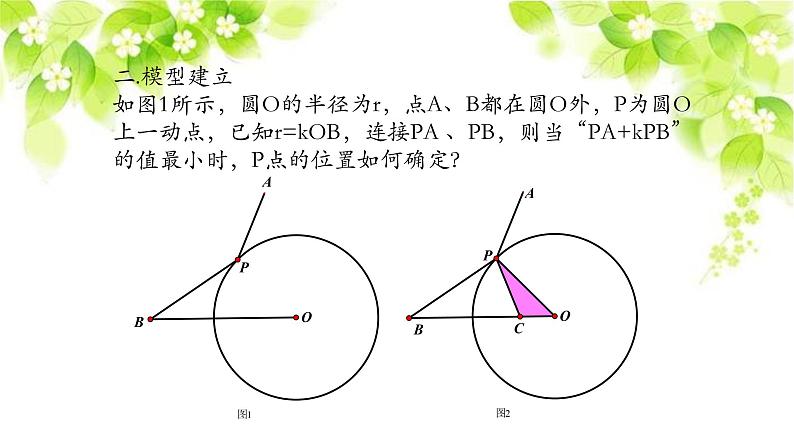
二.模型建立如图1所示,圆O的半径为r,点A、B都在圆O外,P为圆O上一动点,已知r=kOB,连接PA 、PB,则当“PA+kPB”的值最小时,P点的位置如何确定?
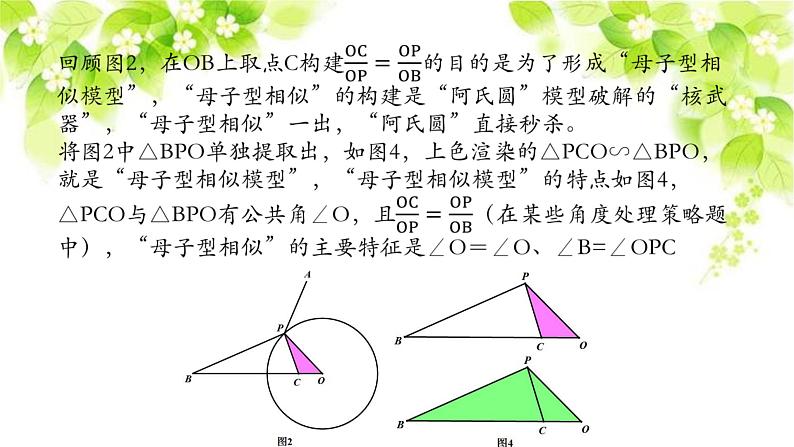
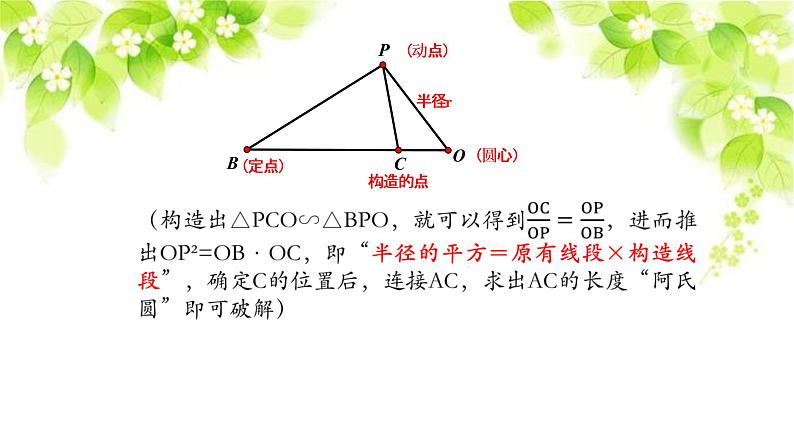
【模型解读】最早见“PA+PB”型的问题是在“将军饮马”问题中,故如何确定“k·PB” 的大小是关键,如图2,在线段OB上截取OC使△BPO与△PCO相似,即k·PB=PC。故本题中“PA+k·PB”的最小值可以转化为“PA+PC”的最小值,其中A与C为定点,P为动点,故当A、P、C三点共线时,“PA+PC”值最小,如图3
例2:已知扇形COD中,∠COD=90°,OC=6,OA=3,OB=5,点P是弧CD上一点,求2PA+PB的最小值?
例8:在平面直角坐标系中,A(2,0),B(0,2),C(4,0),D(3,2),P是△AOB外部的第一象限内一动点,且∠BPA=135°,则2PD+PC的最小值为?
例9:如图1,在Rt△ABC中,AB=9,BC=8,∠ABC=60°,圆A的半径为6,P是圆A上的动点,连接PB、PC,则3PC+2PB的最小值为?
五.“阿氏圆”实战演练练1:如图,在边长为4的正方形ABCD内,内切圆记为圆O,P是圆O上一动点,则2PB+PC的最小值为?
练2:如图,等边△ABC的边长为6,内切圆记为圆O,P是圆O上一动点,则2PB+PC的最小值为?
中考数学复习微专题六几何最值问题模型五线段和差——阿氏圆问题课件: 这是一份中考数学复习微专题六几何最值问题模型五线段和差——阿氏圆问题课件,共11页。PPT课件主要包含了基本模型,针对训练,针对巩固等内容,欢迎下载使用。
几何模型4.3 “阿氏圆”模型(与圆有关的模型)-中考数学二轮复习必会几何模型剖析(全国通用)课件PPT: 这是一份几何模型4.3 “阿氏圆”模型(与圆有关的模型)-中考数学二轮复习必会几何模型剖析(全国通用)课件PPT,共42页。PPT课件主要包含了∴DEDF,B加权点,A非加权点,M破题点,BC权心线,破题通法,求求AE的长,解题步骤五部曲,连连接AE,AE为所求线段等内容,欢迎下载使用。
初中数学中考复习 专题39 几何最值之阿氏圆问题【热点专题】课件PPT: 这是一份初中数学中考复习 专题39 几何最值之阿氏圆问题【热点专题】课件PPT,共11页。












