2022年中考数学复习：胡不归问题 课件

这是一份2022年中考数学复习：胡不归问题 课件，共14页。PPT课件主要包含了一故事背景，二模型概述，步骤如下，课后练习等内容，欢迎下载使用。
一.教学目标1.知识与技能：让学生学会转化并会求PA+ PB （0＜ ＜1）的和的最小值2.过程与方法：学生通过探索总结归纳出胡不归问题的基本步骤，得出实质，学会转化、数形结合的思想3.情感态度、价值观：通过探究，提高学生的数学素养,培养全体学生学习的兴趣和他们的逻辑思维综合能力
二.教学重点：1.胡不归问题的解法与步骤 三.教学难点：1.将PA+ PB （0＜ ＜1）的和转化成垂线段
传说一个身在异乡的青年得到她母亲病重的消息，便日夜赶路返乡，因返乡心切，选择了全是砂石的直线路程，而没有选择先坐车走一段再走砂石路回家。当他赶到家时，他的母亲才刚刚咽气，在弥留之际，她在不停唠叨着“胡不归？胡不归？“ 冷静下来后，青年思考，这样回家虽然路程最短，但是时间较长，选择怎样的路线回家会大大缩短时间，这就是流传千百年的“胡不归问题”。
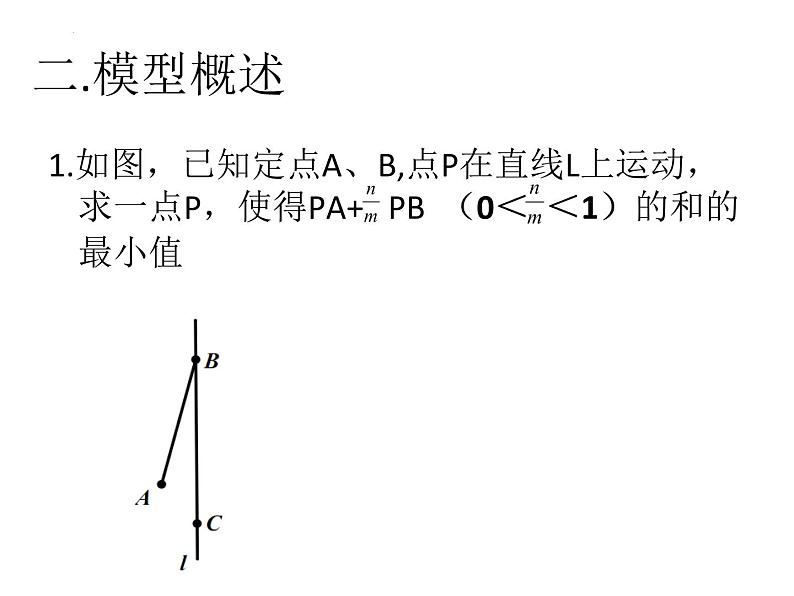
1.如图，已知定点A、B,点P在直线L上运动，求一点P，使得PA+ PB （0＜ ＜1）的和的最小值
①在PB的一侧，PA的异侧作直线L ,构造一个角度α，使得sinα= ②过点P作PE⊥L 于E,得PE= PB，则PA+ PB =PA+PE③过点A作AD⊥L 于D交直线L于点P ,此时垂线段AD的长即为所求最小值
第一步：将所求线段和改写为 的形式（0＜ ＜1）第二步：在PB的一侧，PA的异侧，构造一个角度α，使得sinα= 第三步：过A作第二步所构造的角的一边垂线，该垂线段即为所求最小值第四步：计算完成实质：垂线段最短问题关键：将PA+ PB （0＜ ＜1）的和转化成垂线段
1.如图，正方形ABCD的对角线BD上有一点P，AB=6，则2PA+PB的最小值为（ ）
2PA+PB=2（PA+ PB）作BE使∠PBE=30°，过点p作PF⊥BE，PF= PB显然A、P、F共线时PA+ PB最小。此时PA+ PB=AF利用三角形关系容易求出AF= （3 + 3 ）
1.如图，∠B=15°，BC=6， AB边上一动点D，连结DC,则DC+ DB的和的最小值为（ ）
2. 如图，点E是菱形对角线AC上的动点，AB=5,AC=4 （不与A,C重合）,则EB+ EA的最小值为_________
五，本节课同学们有什么收获？谈谈你的想法？
1.胡不归的解法2.胡不归的步骤及实质3.不归的的关键
1． 如图，直线y=2x+4与x轴y轴分别交于点A，点B，点H为y轴上一动点，连接HA，则2(HA+ HB)的最小值为