2023北京大兴高三（上）期末数学（教师版）

2023北京大兴高三（上）期末

数    学

第一部分 （选择题  共40分）

一、选择题共10小题，每小题4分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知集合，则

（A）                （B） 

（C）                 （D）

（2）下列函数中，既是奇函数又在定义域上是增函数的为

（A）                         （B）

（C）                          （D）

（3）在展开式中，的系数为

（A）                               （B）

（C）                             （D）

（4）记为等差数列的前项和．已知，，则

（A）为递减数列                 （B）

（C）有最大值                     （D）

（5）已知抛物线上一点与其焦点的距离为5，则点到x轴的距离等于

（A）                              （B）

（C）                              （D）

（6）“”是“直线与圆相切”的

（A）充分而不必要条件              （B）必要而不充分条件 

（C）充分必要条件                    （D）既不充分也不必要条件

（7）某圆锥曲线C是椭圆或双曲线，若其中心为坐标原点，对称轴为坐标轴，且过和两点，则曲线C的离心率等于

（A）                              （B）

（C）                             （D）

（8）已知数列中，，，，则下列结论错误的是

（A）                           （B）

（C）是等比数列                  （D）

（9）“赵爽弦图”是我国古代数学的瑰宝，它是由四个全等的直角三角形和一个正方形构成。现仿照赵爽弦图，用四个三角形和一个小平行四边形构成如下图形，其中，E，F，G，H分别是DF，AG，BH，CE的中点，若，则等于

（A）                          

（B）

（C）                 

（D）

（10）已知函数，给出下列结论：①是周期函数；②最小值是；③的最大值是；④曲线是轴对称图形．则正确结论的序号是

（A）①③                               （B）②④

（C）①②③                             （D）②③④

第二部分 （非选择题  共110分）

二、填空题共5小题，每小题5分，共25分。

（11）已知复数满足，则       ．

（12）一个袋子中装有5个不同颜色但大小相同的球，其中2个红球，3个白球，从中依次摸出 2个球，则在第一次摸到红球的条件下，第二次摸到白球的概率是    ．

（13）在中，．若，则    ；若满足条件的三角形有两个，则的一个值可以是        ．

（14）已知函数若，则函数的值域为       ；若函数恰有三个零点，则实数a的取值范围是     

（15）在正方体中，为正方形的中心. 动点沿着线段从点向点移动，有下列四个结论：

①存在点，使得；                   

②三棱锥的体积保持不变；

③的面积越来越小；

④线段上存在点，使得直线⊥直线，且直线⊥直线；

则上述结论中，所有正确结论的序号是         

三、解答题共6小题，共85分。解答应写出文字说明，演算步骤或证明过程。

（16）（本小题14分）

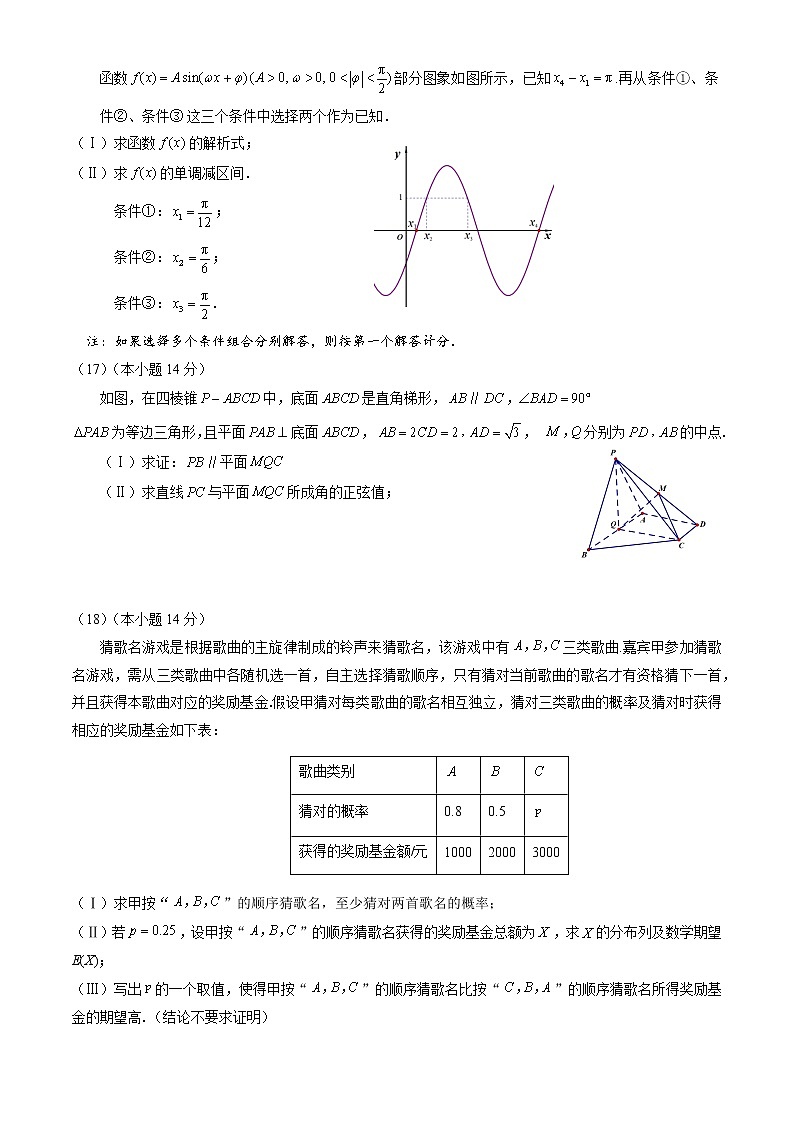
函数部分图象如图所示，已知.再从条件①、条件②、条件③ 这三个条件中选择两个作为已知．

（Ⅰ）求函数的解析式；

（Ⅱ）求的单调减区间．

条件①：；

条件②：；

条件③：．

注：如果选择多个条件组合分别解答，则按第一个解答计分． 

（17）（本小题14分）

如图，在四棱锥中，底面是直角梯形，

为等边三角形，且平面底面，， 分别为的中点.

（Ⅰ）求证：平面

（Ⅱ）求直线与平面所成角的正弦值；

（18）（本小题14分）

猜歌名游戏是根据歌曲的主旋律制成的铃声来猜歌名，该游戏中有三类歌曲.嘉宾甲参加猜歌名游戏，需从三类歌曲中各随机选一首，自主选择猜歌顺序，只有猜对当前歌曲的歌名才有资格猜下一首，并且获得本歌曲对应的奖励基金.假设甲猜对每类歌曲的歌名相互独立，猜对三类歌曲的概率及猜对时获得相应的奖励基金如下表：

（Ⅰ）求甲按“”的顺序猜歌名，至少猜对两首歌名的概率；

（Ⅱ）若，设甲按“”的顺序猜歌名获得的奖励基金总额为，求的分布列及数学期望E(X)；

（Ⅲ）写出的一个取值，使得甲按“”的顺序猜歌名比按“”的顺序猜歌名所得奖励基金的期望高.（结论不要求证明）

（19）（本小题14分）

已知椭圆经过直线与坐标轴的两个交点.

（Ⅰ）求椭圆的方程；

（Ⅱ）为椭圆的右顶点，过点的直线交椭圆于点，过点作轴的垂线分别与直线交于点，求证：为线段的中点.

（20）（本小题15分）

已知函数

（Ⅰ）当函数在处的切线斜率为0时，求的值；

（Ⅱ）判断函数单调性并说明理由；

（Ⅲ）证明：对有成立.

（21）（本小题14分）

已知数列，为从1到2022互不相同的整数的一个排列，设集合,中元素的最大值记为,最小值记为.

（Ⅰ）若数列为:,且，写出的值；

（Ⅱ）若，求M的最大值及N的最小值；

（Ⅲ）若，试求M的最小值.

参考答案

一、选择题（共10小题，每小题4分，共40分）

二、填空题（共5小题，每小题5分，共25分）

（11）

（12）

（13）；之间的任意一个角都可以

（14）；

（15）①②③（只写对一个2分，只写对二个3分）

三、解答题（共6小题，共85分）

（16）（本小题14分）

解：由图可知，

所以.                        ……………………………… 2分

又知.                    ……………………………… 4分

所以.

（Ⅰ）若选择条件①②，即，.

因为.

由图可知，即.…………………… 6分

因为，

所以当时，.……………………………… 8分

所以.

又因为.

所以.            ……………………………… 10分

所以.

若选择条件①③, 即，.

因为.

由图可知，即.

因为，

所以当时，.

所以. 

又因为,

所以.

所以.

若选择条件②③, 即，.

因为,

由图可知，当时取得最大值，

即，

由

得，

因为，

所以.

又，

所以.

所以.

（Ⅱ）因为函数的单调递减区间为 ，，

由，，……………………………… 2分

得，.

所以单调递减区间为，.………………… 4分

（17）（本小题14分）

解：（Ⅰ）连结与交于点，…………………… 1分

      因为底面是直角梯形，, 为的中点.

      所以，即为平行四边形，

      所以点是中点，连结，

      所以.           …………………… 3分              

      又因为平面，平面，

      所以平面.…………………… 5分

（Ⅱ）因为为等边三角形，为的中点，所以.

又面面，

面面，

      所以面，

      又因为，所以.

      如图建立空间直角坐标，…………………… 2分

      可知，，，，

      易知，…………………… 4分

     设面的法向量为，

     且，，

     所以，…………………… 6分

     设与平面所成角为，…………………… 7分

     则，…………………… 9分

     所以与平面所成角的正弦值为.

（18）（本小题14分）

解：（Ⅰ）设“甲按“”的顺序猜歌名至少猜对两首歌名”为事件，……… 1分

则.…………………… 5分

所以，甲按“”的顺序猜歌名至少猜对两首歌名的概率为0.4.

（Ⅱ）的所有可能取值为0，1000，3000，6000，…………………… 1分

，

，

，

，…………………… 5分

所以随机变量的分布列为

所以.…………………… 7分

（Ⅲ）均可. …………………… 2分

（19）（本小题14分）

解：（Ⅰ）直线与坐标轴的两个交点为，…………………… 2分

           由于，所以，，…………………… 4分

         所以椭圆的方程为.…………………… 5分

（Ⅱ）设过点的直线为，由题意直线斜率存在，

        设方程为，即.…………………… 1分

        由，消元得，

        整理得.…………………… 2分

由 ，可得.……………3分

设，则

， .…………………… 4分

由题意，将，代入得，…………………… 5分

      直线的方程为，…………………… 6分

令得，…………………… 7分

      所以

       所以，点是线段的中点. …………………… 9分

（20）（本小题15分）

解：（Ⅰ），

所以，…………………… 2分

由，得，

所以.…………………… 4分

（Ⅱ）函数在单调递增. …………………… 1分

        因为，所以函数定义域为.…………………… 2分

       ，

因为.…………………… 4分

因为，所以.        …………………… 5分

因此函数在区间上单调递增.

（Ⅲ）证明：当时，显然有，不等式成立；……………… 1分

当时，不妨设，…………………… 2分

由于函数在区间上单调递增，

所以，

又，

则

.…………………… 4分

因为，所以，

所以，

所以.…………………… 6分

综上，对任意的，成立.

（21）（本小题14分）

解：（Ⅰ），.…………………… 4分

（Ⅱ）最小值为6，的最大值6063.

证明：对于1，2，…，2021，2022的一个排列，

若，则A中的每一个元素为，

由题意，

那么，对于任意的，总有.

同理，由题意，

那么，对于任意的，总有，…………………… 4分

当时，满足:，.…………………… 5分

（Ⅲ）M的最小值为6069.

由于，对于1，2，……，2021，2022的一个排列，

A中的每一个元素为，

由题意，

对于任意的，都有

，

即，.…………………… 2分

构造数列：，，

对于数列，设任意相邻6项的和为T，则

，或

若，则

==6069，

若，则

+

=，（）

所以，即对这样的数列，，

又，所以的最小值为.…………………… 5分