2023北京房山高三（上）期末数学（教师版）

2023北京房山高三（上）期末

数    学

第一部分（选择题  共40分）

一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.

1. 已知集合，，则（    ）

A.  B.  C.  D.

2. 若复数满足，则在复平面内对应的点位于（    ）

A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

3. 已知数列满足，且，则数列的前四项和的值为（    ）

A.  B.

C.  D.

4 已知函数，则（    ）

A. 图象关于原点对称，且在上是增函数

B. 图象关于原点对称，且在上是减函数

C. 图象关于轴对称，且在上是增函数

D. 图象关于轴对称，且在上是减函数

5. 若角、是锐角三角形的两个内角，则下列各式中一定成立的是（    ）

A  B.

C.  D.

6. 设平面与平面相交于直线，直线在平面内，直线在平面内，且.则“”是“”的（    ）

A. 充分不必要条件 B. 必要不充分条件

C. 充分必要条件 D. 既不充分也不必要条件

7. 若抛物线（）上一点到抛物线的准线和对称轴的距离分别为5和3，则的值为（    ）

A. 1 B. 2 C. 1或9 D. 2或9

8. 已知半径为1的动圆经过坐标原点，则圆心到直线的距离的最大值为（    ）

A. 1 B. 2 C. 3 D. 4

9. 某教学软件在刚发布时有100名教师用户，发布5天后有1000名教师用户.如果教师用户人数与天数之间满足关系式：，其中为常数，是刚发布时的教师用户人数，则教师用户超过20000名至少经过的天数为（    ）（参考数据：）

A 9 B. 10 C. 11 D. 12

10. 在中，，，则的取值范围为（    ）

A.  B.  C.  D.

第二部分（非选择题  共110分）

二、填空题共5小题，每小题5分，共25分.

11. 函数的定义域是______.

12. 的展开式中常数项是______.（用数字作答）

13. 若双曲线的离心率为2，则该双曲线的渐近线方程为______.

14. 若函数存在最小值，则的一个取值为______；的最大值为______.

15. 函数的图象可以近似表示某音叉的声音图象.给出下列四个结论：

①是函数的一个周期；   

②的图象关于直线对称；

③的图象关于点对称；   

④上单调递增.

其中所有正确结论序号是______.

三、解答题共6小题，共85分.解答应写出文字说明，演算步骤或证明过程.

16. 在中，是边上一点，，，，.

（1）求的长；

（2）求的面积.

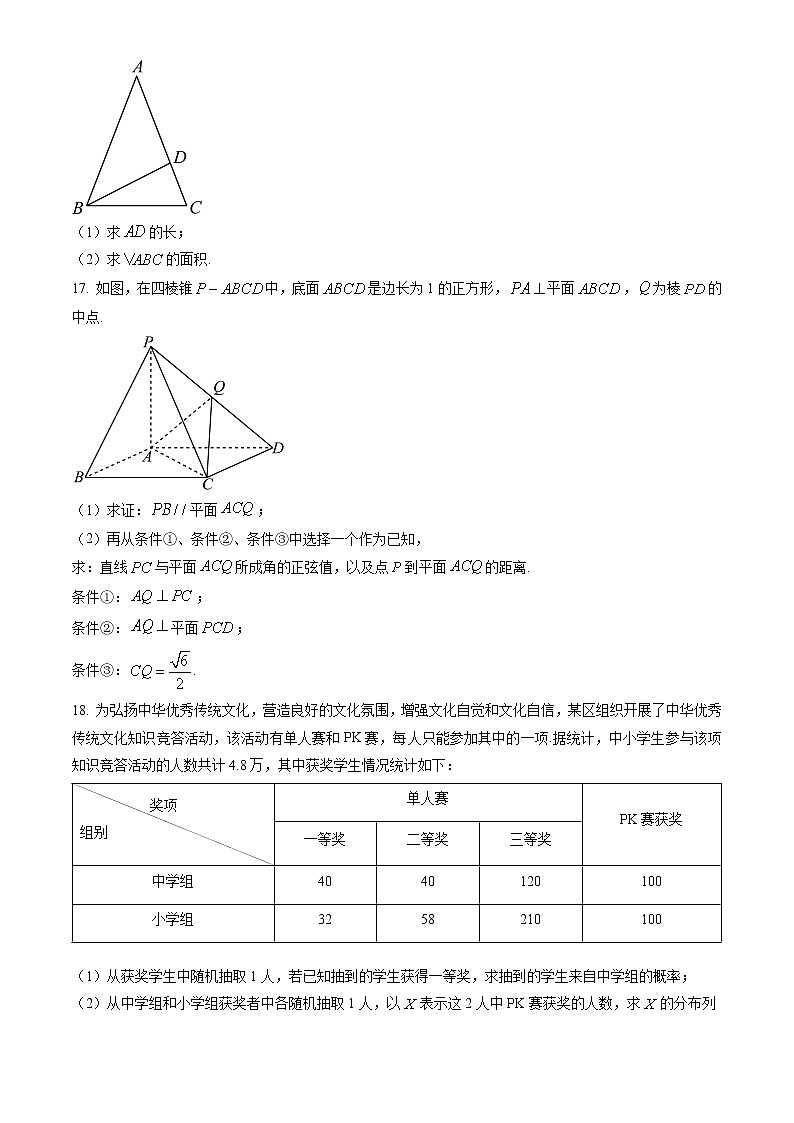
17. 如图，在四棱锥中，底面是边长为1的正方形，平面，为棱的中点.

（1）求证：平面；

（2）再从条件①、条件②、条件③中选择一个作为已知，

求：直线与平面所成角的正弦值，以及点到平面的距离.

条件①：；

条件②：平面；

条件③：.

18. 为弘扬中华优秀传统文化，营造良好的文化氛围，增强文化自觉和文化自信，某区组织开展了中华优秀传统文化知识竞答活动，该活动有单人赛和PK赛，每人只能参加其中的一项.据统计，中小学生参与该项知识竞答活动的人数共计4.8万，其中获奖学生情况统计如下：

（1）从获奖学生中随机抽取1人，若已知抽到的学生获得一等奖，求抽到的学生来自中学组的概率；

（2）从中学组和小学组获奖者中各随机抽取1人，以表示这2人中PK赛获奖的人数，求的分布列和数学期望；

（3）从获奖学生中随机抽取3人，设这3人中来自中学组的人数为，来自小学组的人数为，试判断与的大小关系.（结论不要求证明）

19. 已知函数（）.

（1）当时，求曲线在点处的切线方程；

（2）求函数的单调区间；

（3）若函数恰有一个零点，则的取值范围为______.（只需写出结论）

20. 已知椭圆：经过点，且点到两个焦点的距离之和为8.

（1）求椭圆的方程；

（2）直线：与椭圆分别相交于两点，直线，分别与轴交于点，.试问是否存在直线，使得线段的垂直平分线经过点，如果存在，写出一条满足条件的直线的方程，并证明；如果不存在，请说明理由.

21. 若对，，当时，都有，则称数列受集合制约.

（1）若，判断是否受制约，是否受区间制约；

（2）若，受集合制约，求数列的通项公式；

（3）若记：“受区间制约”，：“受集合制约”，判断是否是的充分条件，是否是的必要条件，并证明你的结论.

参考答案

第一部分（选择题  共40分）

一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.

1. 【答案】B

【解析】

【分析】解不等式求得集合，进而求得.

【详解】，解得，所以，

所以.

故选：B

2. 【答案】A

【解析】

【分析】根据给等式求出用表示，然后运用复数的除法运算解决.

【详解】，所以复数在复平面上的点为，所以点在第一象限

故选：A

3. 【答案】C

【解析】

【分析】由题意是首项为2、公比为的等比数列，利用等比数列前n项和公式求的值.

【详解】由题设是首项为2、公比为的等比数列，即，

所以.

故选：C

4. 【答案】B

【解析】

【分析】根据定义判断奇偶性，由解析式判断单调性，即可得答案.

【详解】由且定义域为R，

所以为奇函数，即关于原点对称，

又在R上递减，故在上是减函数.

故选：B

5. 【答案】D

【解析】

【分析】根据题设可得，结合诱导公式判断内角、对应三角函数值的大小关系.

【详解】由锐角三角形知：且，

所以，

则，即，且，即.

又已知角的大小不确定，故A、B不一定成立，而C错，D对.

故选：D

6. 【答案】A

【解析】

【分析】根据线面、面面垂直的判定及性质判断题设条件间的推出关系，结合充分、必要性定义确定答案.

【详解】已知且，

当时，则，而，故，充分性成立；

当时，

若相交，又，且l、n在β内，则，且，故；

若平行，不一定成立，即不能确定；

所以必要性不成立，

故“”是“”的充分不必要条件.

故选：A

7. 【答案】C

【解析】

【分析】由题设抛物线准线为且对称轴为x轴，令且，结合已知列方程组求参数p即可.

【详解】由抛物线（）知：准线为且对称轴为x轴，

不妨令且，则，可得，

所以，解得或，均满足题设.

故选：C

8. 【答案】C

【解析】

【分析】利用圆上的点到直线的距离的最值可求解.

【详解】由题设，半径为1的动圆经过坐标原点，

可知圆心的轨迹为以原点为圆心，半径为1的圆，即

则该圆上的点到直线的距离的最大值为

又，，，即

故距离的最大值为3

故选：C

9. 【答案】D

【解析】

【分析】根据已知条件求得，结合及指对数关系、对数运算性质求解集，即可得结果.

【详解】由题设，可得，

所以，则，故，

所以教师用户超过20000名至少经过12天.

故选：D

10. 【答案】D

【解析】

【分析】设，利用余弦定理可求得，根据向量数量积定义可得，利用三角形三边关系可求得的范围，结合二次函数性质可求得结果.

【详解】设，则，

由余弦定理得：，

；

，，，

即的取值范围为.

故选：D.

第二部分（非选择题  共110分）

二、填空题共5小题，每小题5分，共25分.

11. 【答案】

【解析】

【分析】根据分式、对数的性质列不等式组求定义域即可.

【详解】由题设，故，

所以定义域为.

故答案为：

12. 【答案】

【解析】

【分析】根据的展开式的通项公式可求出结果.

【详解】的展开式的通项为，

令，得，

所以的展开式中常数项是.

故答案为：.

13. 【答案】

【解析】

【分析】根据离心率求得，然后求得双曲线的渐近线方程.

【详解】依题意，，

，

则双曲线的渐近线方程为.

故答案为：

14. 【答案】    ①. 0（答案不唯一）    ②. 4

【解析】

【分析】根据分段函数的性质，结合绝对值、二次函数的性质，讨论m范围及存在最小值确定m的范围，进而确定答案.

【详解】对于，在上递减，上递增，在R上的最小值为0；

对于，开口向上且对称轴为，

所以，在上递减，上递增，在R上的最小值为；

综上，对于f(x)：当时，在上递减，上递增，

此时恒成立，所以不存在最小值；

当时，在上递减，上递增，此时最小值为0；

当时，在上递减，,上递增，且，

又，

若时，，此时最小值为0；

若时，，此时最小值为0；

若时，，此时最小值为0；

若时，，此时最小值为0；

若时，，此时不存在最小值；

综上，，故m的最大值为4.

故答案为：0（答案不唯一），4

15. 【答案】①③④

【解析】

【分析】①应用诱导公式判断判断是否成立即可；②③、的等量关系判断正误；④判断，，上，，对应单调性，即可判断.

【详解】①，

所以是函数的一个周期，正确；

，

所以不关于直线对称，而关于点对称，②错误，③正确；

④，则，，，

而在、、均递增，故在上单调递增，正确.

故答案为：①③④

三、解答题共6小题，共85分.解答应写出文字说明，演算步骤或证明过程.

16. 【答案】（1）2    （2）

【解析】

【分析】（1）中，根据余弦定理求的长；

（2）中，根据余弦定理求，即可求，再根据三角形的面积公式求解.

【小问1详解】

因为，

则，，，

中，,

即，解得：或（舍），

所以；

【小问2详解】

，

因为

所以，，

所以.

17. 【答案】（1）证明见解析   

（2）答案见解析

【解析】

【分析】（1）连接，交于，连接，由中位线性质有，再由线面平行的判定证结论；

（2）根据所选的条件求得，以为原点，为x、y、z轴建立空间直角坐标系，应用空间向量夹角的坐标表示求线面角正弦值，点面距离的向量求法求到平面的距离.

【小问1详解】

连接，交于，连接，

底面是正方形，故是的中点，又为棱的中点，

所以，在△中，而面，面，

所以平面.

小问2详解】

选①：若分别是中点，连接，

由为棱的中点且底面是正方形，易知：，

又共线且，故，

所以为平行四边形，故，而，则，

在△中，垂直平分，故，即，

由，故，

又平面，平面，则，又，

以为原点，为x、y、z轴建立空间直角坐标系，

则，故，

令为面的一个法向量，则，令，，

所以，即直线与平面所成角的正弦值为，

所以点到平面的距离.

选②：平面，平面，则，为棱的中点，

在△中，垂直平分，故，

又平面，平面，则，又，

以为原点，为x、y、z轴建立空间直角坐标系，

则，故，

令为面的一个法向量，则，令，，

所以，即直线与平面所成角的正弦值为，

所以点到平面的距离.

选③：由平面，平面，则，又，

由，面，故面，面，

所以，

在中，，则，故，

又平面，则，在中，，即，

又平面，平面，则，又，

以为原点，为x、y、z轴建立空间直角坐标系，

则，故，

令为面的一个法向量，则，令，，

所以，即直线与平面所成角的正弦值为，

所以点到平面的距离.

18. 【答案】（1）   

（2）分布列见解析，期望为   

（3），理由见解析

【解析】

【分析】（1）应用条件概率公式求概率即可；

（2）由题设可能值为，结合表格数据及超几何分布概率公式求分布列，进而求期望；

（3）由，应用方差的性质判断的数量关系即可.

【小问1详解】

若事件表示抽到的学生获得一等奖，事件表示抽到的学生来自中学组，

所以抽到的1个学生获得一等奖，学生来自中学组的概率为，

由表格知：，则.

【小问2详解】

由题意，可能值为，

，，，

的分布列如下：

所以.

【小问3详解】

由题设知，所以.

19. 【答案】（1）   

（2）答案见解析    （3）.

【解析】

【分析】（1）利用导数的几何意义求在点处的切线方程；

（2）由题设，讨论参数a，结合不同区间上符号确定的单调区间；

（3）根据（2）所得的单调性，讨论参数a，结合零点存在性定理判断零点的个数，即可得参数范围.

【小问1详解】

由题设，则，

所以，，故曲线在点处切线方程为.

【小问2详解】

由，

当时，，则时，时，

所以在上递减，上递增；

当时，令，可得或，

若，即时，、上，上，

所以在、上递增，上递减；

若，即时，在R上恒成立，即在R上递增；

若，即时，、上，上，

所以在、上递增，上递减；

综上，，在上递减，上递增；

，在、上递增，上递减；

，在R上递增；

，在、上递增，上递减；

【小问3详解】

由（2），当时，，而趋向、时趋向于，

所以，在、各有一个零点，共两个零点，不合题设；

当时，，

在上，趋向时趋向于，

所以，此时在有一个零点，满足题设；

当时，极大值，极小值，趋向时趋向于，

所以，在有一个零点，满足题设；

当时，，趋向时趋向于，

所以，在R上有一个零点，满足题设；

当时，极大值，极小值，趋向时趋向于，

所以，在上有一个零点，满足题设；

综上，函数恰有一个零点，.

20. 【答案】（1）   

（2）（答案不唯一）

【解析】

【分析】（1）根据椭圆的定义，得到，代入，可得，计算得到椭圆的方程.

（2）联立直线与椭圆，利用韦达定理，得到和，再分别利用，得到直线和直线，进而得到与，利用线段的垂直平分线经过点，必有，整理可得，此时，利用韦达定理进行换元，得到，然后，对进行赋值，即可得到满足题意的直线方程.

【小问1详解】

点到两个焦点的距离之和为8，故，,椭圆的方程为，

代入，可得，解得，故椭圆的方程为：

【小问2详解】

由题意，设，联立直线与椭圆的方程，可得，

，整理得，，

化简得，，故；

，，又，

可设直线：，设直线：，

故，，

若线段的垂直平分线经过点，必有，故有

，整理得，

，化简得，，

得到，，

，

，

，

，

，利用韦达定理，得

，

，

，

，

，

，

，

当时，，此时，直线为：，

故令，则必有，满足，

此时，满足题意的直线为：（答案不唯一）

21. 【答案】（1）受制约，不受制约，理由见解析   

（2）且.   

（3）是的充分不必要条件，证明见解析

【解析】

【分析】（1）根据数列新定义，判断、且是否有成立即可判断；

（2）由题设可得，利用等差数列的定义写出的通项公式；

（3）由新定义判断、的推出关系，结合充分、必要性的定义得到结论.

【小问1详解】

由、且，则，而，

显然，则，故受制约，

由、且，

当，即，故；

当，即，故.

故不受制约.

综上，受制约，不受制约.

【小问2详解】

由、且，有，

所以，又，，

故的奇数项、偶数项分别为首项为1、3，且公差均为2的等差数列，

当且，则，

当且，则，

综上，且.

【小问3详解】

结论：是的充分不必要条件，证明如下：

为真：受集合制约，由、且，

当，有成立，则，进而可得：①；

当，有成立，结合①有；

此时，受集合制约；

为真：受集合制约，由、且，有；

而，不一定有成立（反例：且，显然，有），

故不一定受区间制约；

所以，受区间制约，必受集合制约，但受集合制约，不一定受区间制约；

综上，是的充分不必要条件.