考点01 数与式-最新中考数学必背知识手册

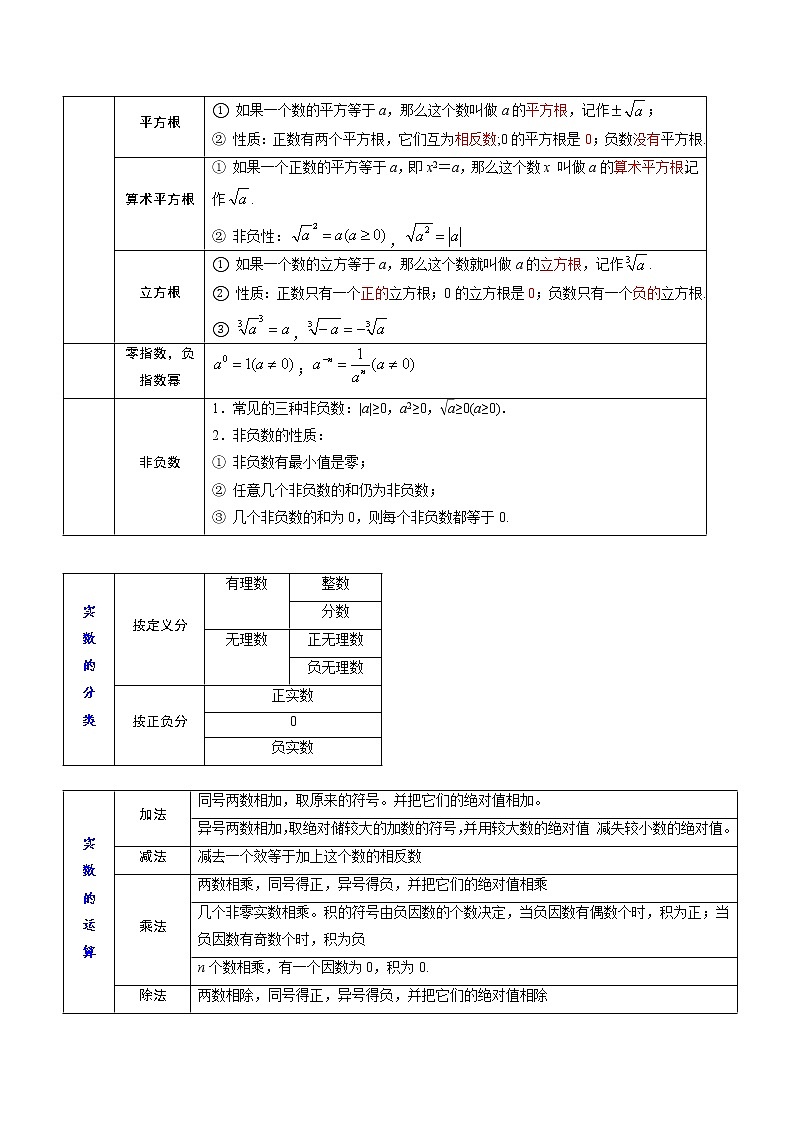
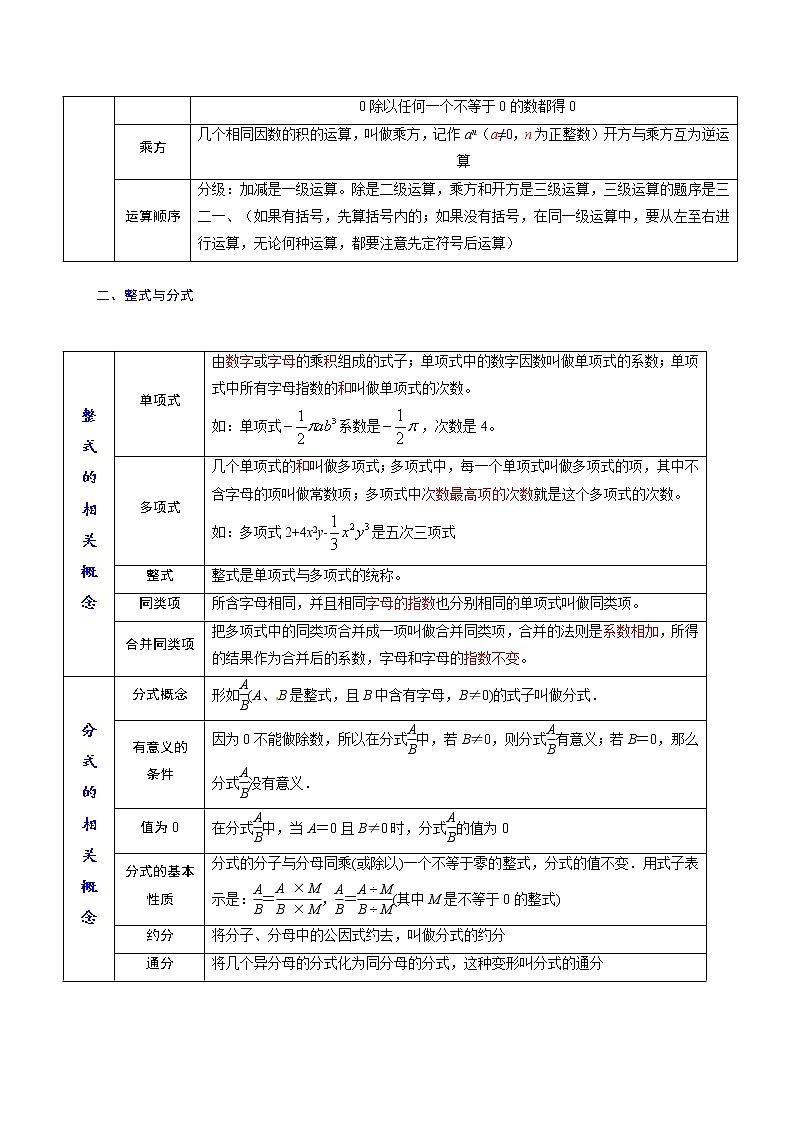
考点01数与式  一、实数与二次根式实数的相关概念正数大于0的数叫做正数意义：表示具有相反意义的量负数在正数前面加上“－”号的数叫做负数数轴规定了原点、正方向和单位长度的直线叫做数轴相反数只有符号不同的两个数，叫做互为相反数（1）若a,b互为相反数，则a+b=0;（2）0的相反数是0;（3）在数轴上，互为相反数的两个数对应的点到原点的距离相等. 绝对值数轴上点a与原点的距离叫做a的绝对值，记作绝对值具有非负性：倒数乘积为1的两个实数互为倒数（1）ab=1⇔a,b互为倒数;（2）0没有倒数;（3）倒数等于它本身的数是1和-1. 科学计数法把一个数写成a×10n（其中1≤|a|＜10，n为整数）的形式无理数无限不循环的小数叫做无理数平方根① 如果一个数的平方等于a，那么这个数叫做a的平方根，记作；② 性质：正数有两个平方根，它们互为相反数;0的平方根是0；负数没有平方根.算术平方根① 如果一个正数的平方等于a，即x2＝a，那么这个数x 叫做a的算术平方根,记作.② 非负性：，立方根① 如果一个数的立方等于a，那么这个数就叫做a的立方根，记作. ② 性质：正数只有一个正的立方根；0的立方根是0；负数只有一个负的立方根. ③ ， 零指数，负指数幂； 非负数1．常见的三种非负数：|a|≥0，a2≥0，≥0(a≥0)．2．非负数的性质：① 非负数有最小值是零；② 任意几个非负数的和仍为非负数；                 ③ 几个非负数的和为0，则每个非负数都等于0. 实数的分类按定义分有理数整数分数无理数正无理数负无理数按正负分正实数0负实数         实数的运算加法同号两数相加，取原来的符号。并把它们的绝对值相加。异号两数相加，取绝对储较大的加数的符号，并用较大数的绝对值 减失较小数的绝对值。减法减去一个效等于加上这个数的相反数乘法两数相乘，同号得正，异号得负，并把它们的绝对值相乘几个非零实数相乘。积的符号由负因数的个数决定，当负因数有偶数个时，积为正；当负因数有奇数个时，积为负n个数相乘，有一个因数为0，积为0.除法两数相除，同号得正，异号得负，并把它们的绝对值相除 0除以任何一个不等于0的数都得0乘方几个相同因数的积的运算，叫做乘方，记作an（a≠0，n为正整数）开方与乘方互为逆运算运算顺序分级：加减是一级运算。除是二级运算，乘方和开方是三级运算，三级运算的题序是三二一、（如果有括号，先算括号内的；如果没有括号，在同一级运算中，要从左至右进行运算，无论何种运算，都要注意先定符号后运算） 二、整式与分式 整式的相关概念单项式由数字或字母的乘积组成的式子；单项式中的数字因数叫做单项式的系数；单项式中所有字母指数的和叫做单项式的次数。如：单项式系数是，次数是4。多项式几个单项式的和叫做多项式；多项式中，每一个单项式叫做多项式的项，其中不含字母的项叫做常数项；多项式中次数最高项的次数就是这个多项式的次数。如：多项式2+4x2y﹣是五次三项式整式整式是单项式与多项式的统称。同类项所含字母相同，并且相同字母的指数也分别相同的单项式叫做同类项。合并同类项把多项式中的同类项合并成一项叫做合并同类项，合并的法则是系数相加，所得的结果作为合并后的系数，字母和字母的指数不变。分式的相关概念分式概念形如(A、B是整式，且B中含有字母，B≠0)的式子叫做分式． 有意义的条件因为0不能做除数，所以在分式中，若B≠0，则分式有意义；若B＝0，那么分式没有意义．值为0在分式中，当A＝0且B≠0时，分式的值为0分式的基本性质分式的分子与分母同乘(或除以)一个不等于零的整式，分式的值不变．用式子表示是：＝，＝(其中M是不等于0的整式)约分将分子、分母中的公因式约去，叫做分式的约分通分将几个异分母的分式化为同分母的分式，这种变形叫分式的通分 整式运算幂的运算同底数幂乘法am·an＝am＋n（a≠0）am＋n＝am·an同底数幂除法＝am－n(m，n是正整数)am－n＝幂的乘方(am)n＝amn（a≠0）amn＝(am)n积的乘方(ab)n＝anbnanbn＝(ab)n乘法公式平方差公式(a＋b)(a－b)＝a2－b2a2－b2＝(a＋b)(a－b)完全平方公式(a±b)2＝a2±2ab＋b2a2±2ab＋b2＝(a±b)2整式加减① 整式的加减其实就是合并同类项；          ② 整式加减的步骤：有括号，先去括号；有同类项，再合并同类项．注意去括号时，如果括号前面是负号，括号里各项的符号要变号．整式乘法① 单项式与单项式相乘：把系数、同底数幂分别相乘，作为积的因式，只在一个单项式里含有的字母，则连同它的指数作为积的一个因式．② 单项式与多项式相乘：m(a＋b＋c)＝ma＋mb＋mC．③ 多项式与多项式相乘：(m＋n)(a＋b)＝ma＋mb＋na＋nb．整式除法① 单项式除以单项式：把系数、同底数幂相除，作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式．② 多项式除以单项式：(a＋b)÷m＝a÷m＋b÷m.因式分解概念把一个多项式化成几个整式的积的形式，叫做多项式的因式分解。和的形式变积的形式因式分解方法提公因式法ma＋mb＋mc＝m(a＋b＋c)（乘法分配律的运用）公式法① 运用平方差公式：a2－b2＝(a＋b)(a－b)．② 运用完全平方公式：a2±2ab＋b2＝(a±b)2.求代数式的值1．一般地，用数值代替代数式里的字母，按照代数式指明的运算关系计算出的结果就叫做代数式的值．2．求代数式的值的基本步骤：① 代入：一般情况下，先对代数式进行化简，再将数值代入；② 计算：按代数式指明的运算关系计算出结果．分式运算分式加减同分母的分式相加减，分母不变，把分子相加减，即±＝.异分母的分式相加减，先通分，变为同分母的分式，然后相加减，即±＝.分式乘除分式乘以分式，用分子的积做积的分子，分母的积做积的分母，即·＝.分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘，即÷＝·＝分式的混合运算在分式的加减乘除混合运算中，应先算乘除，进行约分化简后，再进行加减运算，遇到有括号的，先算括号里面的．运算结果必须是最简分式或整式．    1．比较实数大小的五种方法”（1）绝对值比较法：两个负数比较大小，绝大值大的反而小（2）数轴比较法：在数轴上表示的两个数，右边的数总比左边的数大（3）平方比较法：先将要平方的两个数分别平方，再根据a>0,b>0时，可由a2>b2得到a>b来比较大小。（4）取近以值法：首先对要比较的两个数取近以值通过比较其近似值来比较两个数的大小，（5）差值比较法2．无理数常见的四种类型”：（1）开不尽的数，如，（2）含有π的绝大部分数，如π，（3）具有特定结构的数，如0.10100000(两个1之间依次增加1个0)（4）三角函数数中的一些数，如，，.3．幂运算性质的逆运算① am＋n＝am·an    ② am－n＝   ③ amn＝(am)n  ③ anbn＝(ab)n4．乘法公式的常用变形：① a2＋b2＝(a＋b)2－2ab       ② a2＋b2＝(a－b)2＋2ab ③ (a＋b)2 ＝(a－b)2＋4ab     ④ (a－b)2 ＝(a＋b)2－4ab  5．整体代入法求代数式的值：（1）直接整体代入求值：如果已知的代数式与要求代数式之间含有相同的式子，只要把已知式子的值直接代入到要求的式子中，即可得出结果。（2）把已知式子变形后再整体代入求值：在求代数式的值时，如果题目中所求的代数式与已知代数式成倍数关系，各字母的项的系数对应成比例，就可以把这一部分看作一个整体，再把要求的值的代数式变形后，整体代计算求值。6．分式有意义、无意义和值为零的条件（1）若分式有意义，则B≠0（2）若分式无意义，则B=0（3）若分式 =0，则A=0且B≠0  易错点1：有理数、无理数以及实数的有关概念理解错误，相反数、倒数、绝对值的意义概念混淆。弄不清绝对值与数的分类。选择题考得比较多。1．﹣|﹣2021|＝（　　）A．2021 B．﹣2021 C． D．【答案】B．【解析】解：﹣|﹣2021|＝﹣2021，故选：B．易错点2：关于实数的运算，要掌握好与实数的有关概念、性质，灵活地运用各种运算律，关键是把好符号关；在较复杂的运算中，不注意运算顺序或者不合理使用运算律，从而使运算出现错误。2．下列各式中，正确的是（　　）A．﹣|﹣2|＝2 B．＝±2 C．（﹣2）3＝8 D．（﹣1）2+（﹣1）3＝0【答案】D【解析】解：A．﹣|﹣2|＝﹣2，故错误；B.＝2，故错误；C．（﹣2）3＝﹣8，故错误；D，正确；故选：D．易错点3：平方根、算术平方根、立方根的区别3．的算术平方根是（　　）A．2 B．4 C．±2 D．±4【答案】A【解析】解：＝4，4的算术平方根是2，故选：A．易错点4：科学记数法，精确度。 4．用四舍五入法对数3465983取近似数精确到万位，结果是（　　）A．347 B．3.46 C．3.47×106 D．3.46×107【答案】C【解析】解：3465983＝3.465983×106中，万位上是6，千位上是5，则精确到万位是3.47×106．故选：C．易错点5：五个基本数的计算：0指数，三角函数，绝对值，负指数，二次根式的化简。5．计算：|﹣5|﹣（1﹣π）0+（）﹣1．【答案】解：|﹣5|﹣（1﹣π）0+（）﹣1＝5﹣1+3＝7．【解析】原式第一项绝对值计算，第二项利用零指数幂的法则计算，第三项利用负指数幂的法则计算，计算即可得到结果．易错点6：求分式的值时易忽略分母不为零的条件.6．分式的值为零，则x的值为………………………………………………（   ）A.2                   B.﹣2               C.±2             D.任意实数【答案】A【解析】本题错解考虑到了分子－2为零，而忽视了分式有意义的条件——分母x＋2不为零.分式的值为零的条件应是分子为零且分母不为零，∴由－2＝0，解得x＝±2，又由x＋2≠0，得x≠﹣2，∴x＝2.还有分式无意义的条件是分母为零.易错点7：分式的运算：①运算法则和符号的变化；②分子或分母是多项式时要分解因式且要分解到不能分解为止；③结果应化为最简分式.7．先化简，再求值：（＋2－x）÷，其中x满足x2－4x＋3=0.【答案】原式＝[－]·＝·＝·＝.∵x2－4x＋3=0，∴(x－1)(x－3)＝0，∴x1＝1，x2＝3.又∵x－1≠0，x2＋4x＋4≠0，∴x≠1，x≠﹣2.∴当x＝3时，原式＝＝﹣＝.【解析】本题一处错误是在去括号时，符号出现了错误，括号前面是“﹣”，去掉括号和它前面的“﹣”号，括号里面的每一项都要改变符号，二处错误是原式有意义的条件只考虑了分母不为零，即x－1≠0，而忽视了除数不能为零的条件，即x2＋4x＋4≠0.易错点8：代入求值要使式子有意义。各种数式的计算方法要掌握，一定要注意计算顺序。8．先化简，再求值：（1﹣），其中a满足方程a2﹣a﹣2＝0．【答案】原式＝•＝，解方程a2﹣a﹣2＝0得，a1＝2，a2＝﹣1，当a＝2时，原式＝＝，当a＝﹣1时，分式无意义，则分式的值为．【解析】根据分式的混合运算法则把原式化简，利用因式分解法解出方程，把适合条件的a的值代入计算即可．