广州市天河区天河中学2022-2023学年八年级上学期期末考试数学试题

这是一份广州市天河区天河中学2022-2023学年八年级上学期期末考试数学试题，共14页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
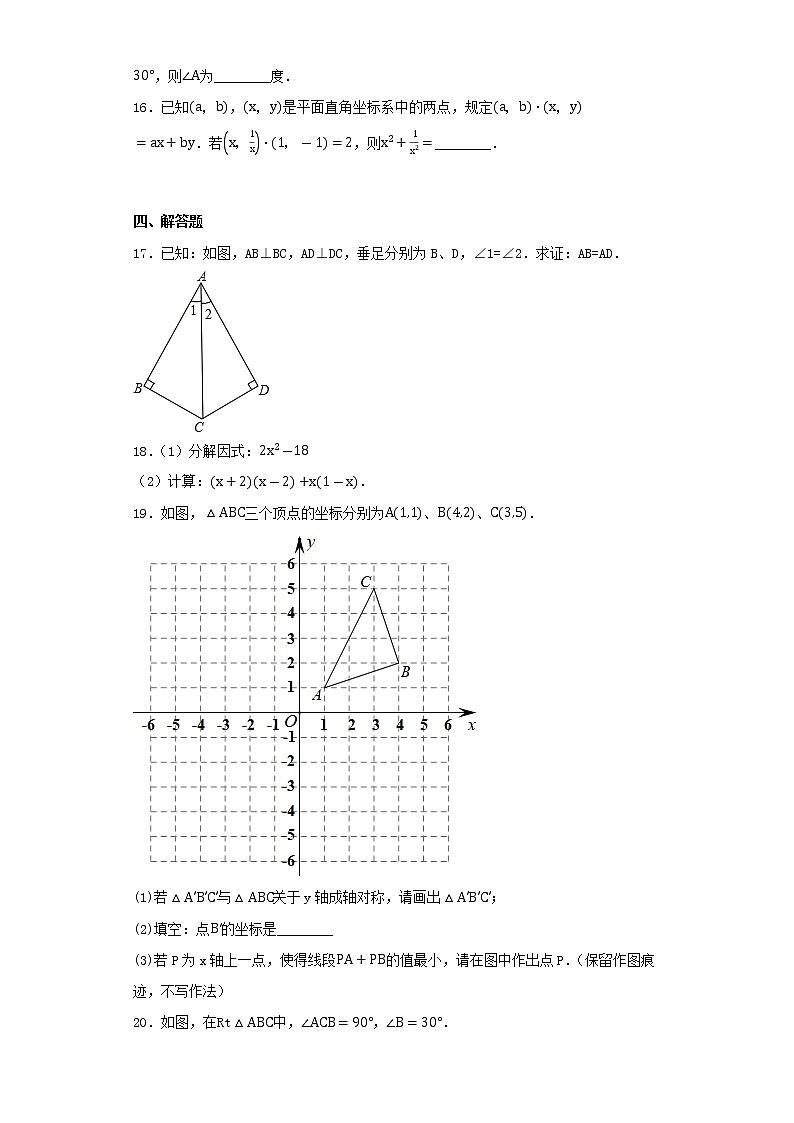
广州市天河区天河中学2022-2023学年八年级上学期期末考试数学试题学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．如图是年北京冬奥运会吉祥物冰墩墩的图形，是轴对称图形的是（   ）A． B．C． D．2．世界上最小的鸟是生活在古巴的吸蜜蜂鸟，它的质量约为0.056盎司．将0.056用科学记数法表示为（   ）A．5.6×10﹣1 B．5.6×10﹣2 C．5.6×10﹣3 D．0.56×10﹣13．下列长度的三根木条首尾相连，能组成三角形的是（　　）A．10，7，5 B．10，7，3 C．10，5，3 D．4，4，104．点关于x轴的对称点是（    ）A． B． C． D．5．下列运算中正确的是（    ）A． B． C． D．6．如图，在和中，已知，在不添加任何辅助线的前提下，要使，只需再添加的一个条件不可以是（    ）A． B． C． D．7．使分式有意义的x的取值范围是（    ）A． B． C． D．8．甲、乙二人做某种机械零件，已知每小时甲比乙少做8个，甲做120个所用的时间与乙做150个所用的时间相等，设甲每小时做x个零件，下列方程正确的是（   ）A． B． C． D． 二、多选题9．如图，于E，于F，若，，则下列结论中正确的是（    ）A． B．平分 C． D．10．若关于x的方程有解，则a的值不能是（    ）A． B． C．1 D．2 三、填空题11．如图：若△ABE≌△ACF，且AB=5，AE=2，则EC的长为______ 12．已知一个n边形的内角和等于720°，则n=______．13．计算：___．14．已知，，则的值是________．15．中，的垂直平分线交于点D，垂足为点E，平分，若，则为________度．16．已知，是平面直角坐标系中的两点，规定．若，则________． 四、解答题17．已知：如图，AB⊥BC，AD⊥DC，垂足分别为B、D，∠1=∠2．求证：AB=AD．18．（1）分解因式：        （2）计算：．19．如图，三个顶点的坐标分别为、、．(1)若与关于y轴成轴对称，请画出；(2)填空：点的坐标是________(3)若P为x轴上一点，使得线段的值最小，请在图中作出点P．（保留作图痕迹，不写作法）20．如图，在中，，．(1)尺规作图：在线段AB上作一点D，使得（不写作法，保留作图痕迹）；(2)若点D到直线的距离为，求的长．21．已知．(1)化简W；(2)若a，3，6恰好是等腰的三边长，求W的值．22．在平面直角坐标系中，，，点C为x轴正半轴上一动点，过点A作交y轴于点E，连接，则平分．(1)如图（1），若，则点E的坐标为________；(2)如图（2），若点C在x轴正半轴上运动，当时，求的度数．
参考答案1．C【分析】根据一个图形沿某一条直线折叠，直线两旁的部分能够完全重合，这个图形叫做轴对称图形，这条直线叫做对称轴去进行分析即可．【详解】解：三个选项中的图形都找不到一条直线能够使直线两旁的部分重合，所以不是轴对称图形；C选项中的图形能够找到这样的一条直线，使直线两旁的部分能够完全重合，所以是轴对称图形；故选：C．【点睛】本题考查了轴对称图形的概念，轴对称图形的关键在于寻找出对称轴，使直线两旁的部分重合是解题的关键．2．B【详解】0.056用科学记数法表示为：0.056=，故选B.3．A【分析】根据三角形三边关系定理：三角形两边之和大于第三边，三角形的两边差小于第三边，可选出答案．【详解】解：A、10＜5+7，能构成三角形，故此选项符合题意；B、3+7＝10，不能构成三角形，故此选项不符合题意；C、3+5＜10，不能构成三角形，故此选项不符合题意；D、4+4＜10，不能构成三角形，故此选项不符合题意．故选：A．【点睛】本题主要考查了三角形的三边关系，熟练掌握三角形三边关系定理：三角形两边之和大于第三边，三角形的两边差小于第三边是解题的关键．4．A【分析】根据关于x轴对称点的性质，“横坐标不变，纵坐标变为相反数”，求解即可．【详解】解：点关于x轴的对称点是，故选：A【点睛】此题主要考查了关于x轴对称点的性质，正确掌握横纵坐标的关系是解题关键．5．D【分析】根据同底数幂的乘法、幂的乘方、积的乘方和同底数幂的除法法则逐一判断即可．【详解】A、，故本选项不符合题意；B、，故本选项不符合题意；C、，故本选项不符合题意；D、，故本选项符合题意．故选：D【点睛】本题考查了同底数幂的乘法、幂的乘方、积的乘方和同底数幂的除法，熟练掌握各运算法则是解题的关键．6．B【分析】添加AC＝AD，利用SAS即可得到两三角形全等；添加∠D＝∠C，利用AAS即可得到两三角形全等，添加∠CBE＝∠DBE，利用ASA即可得到两三角形全等．【详解】解：A、添加AC＝AD，利用SAS即可得到两三角形全等，故此选项不符合题意；B、添加BC＝BD，不能判定两三角形全等，故此选项符合题意；C、添加∠D＝∠C，利用AAS即可得到两三角形全等，故此选项不符合题意；D、添加∠CBE＝∠DBE，利用ASA即可得到两三角形全等，故此选项不符合题意；故选：B．【点睛】此题考查了全等三角形的判定，熟练掌握全等三角形的判定方法是解本题的关键．7．D【分析】根据分式有意义的条件，“分母不能为0”，列不等式求解即可．【详解】解：分式有意义，则，解得，故选：D【点睛】此题考查了分式有意义的条件，解题的关键是掌握分式有意义的条件．8．D【分析】首先用x表示甲和乙每小时做的零件个数，再根据甲做120个所用的时间与乙做150个所用的时间相等即可列出一元一次方程.【详解】解：∵甲每小时做x个零件，∴乙每小时做（x+8）个零件，∵甲做120个所用的时间与乙做150个所用的时间相等，∴，故选D.【点睛】本题考查了分式方程的实际应用，熟练掌握是解题的关键.9．ABD【分析】通过全等三角形的性质，对选项逐个判断即可．【详解】解：∵，∴，又∵，，∴，∴，A选项正确，符合题意；又∵，∴∴，，即平分，B选项正确，符合题意；∴，D选项正确，符合题意；在中，，∴，C选项错误，不符合题意；故选：ABD【点睛】此题考查了全等三角形的判定与性质，解题的关键是灵活掌握全等三角形的判定方法与性质．10．BC【分析】先把分式方程化成整式方程得到，再由分式方程有解得到，即，进一步求出分式方程的解为，再由分式有意义的条件得到，即可得到答案．【详解】解；∵，∴，∴，∴，∵关于x的方程有解，∴，即，∴，又∵，即，∴，∴ ，故选BC．【点睛】本题主要考查了根据分式方程解的情况求参数，正确得到是解题的关键．11．3【详解】解：因为△ABE≌△ACF，所以AC=AB=5，AE=2，所以CE=5-2=3．故答案为3．12．6【分析】根据多边形内角和公式计算即可．【详解】解：由，解得．故答案为：6．【点睛】本题主要考查了多边形内角和定理，掌握多边形内角和定理的计算公式是解题的关键．即多边形的内角和为(n-2)×180°（n≥3的整数）．13．10．【分析】直接根据零指数幂以及负整数指数幂的运算法则化简各数即可．【详解】解：1+9=10．故答案为：10．【点睛】本题主要考查了零指数幂以及负整数指数幂，熟练掌握运算法则是解答此题的关键．14．【分析】对式子进行因式分解，再整体代入求解即可．【详解】解：，将，代入可得，原式，故答案为：【点睛】此题考查了因式分解，代数式求值，解题的关键是掌握因式分解的方法，利用整体代入进行求解．15．【分析】根据线段垂直平分线的性质可得，则，由平分可得，，再根据三角形内角和，求解即可．【详解】解：∵垂直平分，∴，∴，∵平分，∴∴，即由可得，解得，故答案为：【点睛】此题考查了垂直平分线的性质，等腰三角形的性质，三角形内角和的性质，解题的关键是灵活运用相关性质进行求解．16．6【分析】先根据新定义得到，再根据完全平方公式得到，据此即可得到答案．【详解】解：∵，∴，∴，∴，故答案为；6．【点睛】本题主要考查了分式的求值，完全平方公式的变形求值，新定义，正确得到是解题的关键．17．见解析【分析】求出∠B=∠D，根据AAS证△ABC≌△ADC，即可推出结论．【详解】证明：∵AB⊥BC，AD⊥DC，∴∠B=∠D=90°，∵在△ABC和△ADC中， ∴△ABC≌△ADC（AAS），∴AB=AD．18．（1）；（2）【分析】（1）先提取公因式2，再利用平方差公式分解因式即可；（2）先根据平方差公式和多项式乘以单项式的计算法则去括号，然后合并同类项即可．【详解】解：（1）；（2）．【点睛】本题主要考查了分解因式，整式的混合计算，熟知相关计算法则是解题的关键．19．(1)见解析；(2)；(3)见解析． 【分析】（1）根据轴对称性质，作出点，连接即可；（2）根据关于y轴对称的点的性质，即可求解；（3）过点作轴的对称点，连接，交于点，即可求解．【详解】（1）解：如图，即为所求；（2）解：∵∴点的坐标是；（3）解：如图，点即为所求；【点睛】此题考查了轴对称作图以及性质，解题的关键是掌握轴对称的有关性质．20．(1)见解析；(2)． 【分析】（1）作线段的垂直平分线，交于点，点即为所求的点；（2）设的中点为，由题意可得，根据等腰三角形的性质可得，，从而得到为等边三角形，即可求解．【详解】（1）解：如图，点即为所求的点；（2）解：设的中点为，由题意可得，∵，∴，∵，∴∴为等边三角形，∴由题意可得：，∴，∴【点睛】此题考查了尺规作图－垂直平分线，等腰三角形的性质，等边三角形的判定与性质，含角直角三角形的性质，解题的关键是灵活运行相关性质进行求解．21．(1)(2) 【分析】（1）根据分式的混合计算法则求解即可；（2）根据等腰三角形的定义结合构成三角形的条件得到，把代入（1）所求进行求解即可．【详解】（1）解；；（2）解：∵a，3，6恰好是等腰的三边长，∴或，当时，等腰三角形的三边长为3，3，6，不能构成三角形，不符合题意；当时，等腰三角形的三边长为3，6，6，能构成三角形，符合题意；∴，∴．【点睛】本题主要考查了分式的化简求值，等腰三角形的定义，构成三角形的条件，灵活运用所学知识是解题的关键．22．(1)；(2)． 【分析】（1）可证明，从而得出，进而求得；（2）延长至，使得，从而得出，进而得出，在根据三角形内角和求得结果．【详解】（1）解：∵，∴，∴，，∴，∵，，∴，∴，∴，即；（2）解：延长至，使得，如下图：∴，∴，∵，∴，即，∵平分，∴，∵，∴，∴∵，∴，在中，∴，∴．【点睛】本题考查了等腰直角三角形性质，全等三角形的判定和性质，解决问题的关键是作常见辅助线，构造全等或基本定理的条件．