

吉林省长春市榆树市2022-2023学年八年级上学期期末数学试卷(含答案)
展开2022-2023学年吉林省长春市榆树市八年级(上)期末数学试卷
一、选择题(每小题3分,共24分)
1.(3分)四个数0,1,2,13中,无理数的是( )
A.2 B.1 C.13 D.0
2.(3分)下列运算中,正确的是( )
A.a6÷a2=a3 B.﹣a2•a4=a6 C.(ab)3=a3b3 D.(a2)4=a6
3.(3分)小东5分钟内共投篮60次,共进球15个,则小东进球的频率是( )
A.0.25 B.60 C.0.26 D.15
4.(3分)下列各式从左到右的变形,属于因式分解的是( )
A.x2+2x+3=(x+1)2+2 B.(x+y)(x﹣y)=x2﹣y2
C.x2﹣xy+y2=(x﹣y)2+xy D.2x﹣2y=2(x﹣y)
5.(3分)如图所示,在△ABC中,∠ACB=90°,分别以AB、BC、AC为边向外作正方形,若三个正方形的面积分别为225、400、S,则S的值为( )
A.25 B.175 C.600 D.625
6.(3分)如图,若AB∥CD,AD=CD,∠1=70°,则∠2的度数是( )
A.70° B.40° C.35° D.20°
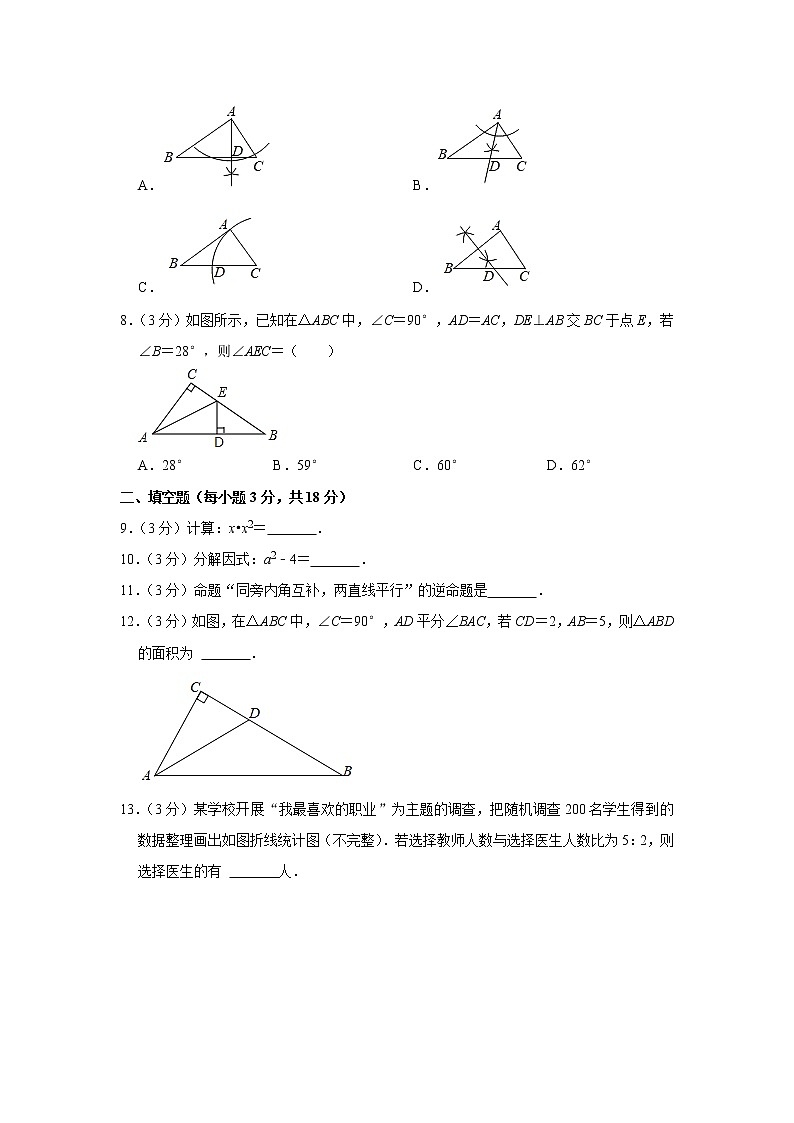
7.(3分)在△ABC中,∠BAC=90°,AB>AC,∠B≠30°,用无刻度的直尺和圆规在BC边上找一点D,使AD=BD,下列作法正确的是( )
A. B.
C. D.
8.(3分)如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC=( )
A.28° B.59° C.60° D.62°
二、填空题(每小题3分,共18分)
9.(3分)计算:x•x2= .
10.(3分)分解因式:a2﹣4= .
11.(3分)命题“同旁内角互补,两直线平行”的逆命题是 .
12.(3分)如图,在△ABC中,∠C=90°,AD平分∠BAC,若CD=2,AB=5,则△ABD的面积为 .
13.(3分)某学校开展“我最喜欢的职业”为主题的调查,把随机调查200名学生得到的数据整理画出如图折线统计图(不完整).若选择教师人数与选择医生人数比为5:2,则选择医生的有 人.
14.(3分)如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠DAE=72°,则∠EDC的度数为 .
三、解答题(本大题共10小题,共78分)
15.(8分)计算:
(1)(2m2﹣m)2÷(﹣m2);
(2)(2x+5y)(3x﹣2y).
16.(6分)因式分解:x2﹣4xy+4y2.
17.(7分)先化简,再求值:2(a+1)(a﹣1)﹣a(2a﹣3),其中a=-16.
18.(6分)图①、图②均是4×4的正方形网格,每个小正方形的顶点称为格点,小正方形的边长均为1,点A、点B均在格点上,在给定的网格中按要求画图,所画图形的顶点均在格点上.
(1)在图①中,以线段AB为腰画一个等腰三角形.
(2)在图②中,以线段AB为底画一个等腰三角形.
19.(6分)如图,△ABC中,AB=AC,DE垂直平分AC,若∠A=30°,求∠BCD的度数.
20.(8分)如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB.
(1)求修建的公路CD的长;
(2)若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?
21.(7分)如图,在△ABC中,AB=AC,AD是BC边上的中线,AE⊥BE于点E,且BE=12BC.求证:AB平分∠EAD.
22.(8分)某校数学兴趣小组为了解学生对A:新闻、B:体育、C:动画、D:娱乐、E:戏曲五类电视节目的喜爱情况,学校随机抽取了n名学生进行调查,规定每人必须并且只能在以上给出的五类中选择一类,并将统计结果绘制了两个不完整的统计图.
节目类型
人数
A
20
B
a
C
52
D
80
E
b
请根据图中所给出的信息解答下列问题:
(1)n= ,a= ,b= .
(2)在扇形统计图中,求节目类型“C”所占的百分数.
(3)在扇形统计图中,求节目类型“D”所对应的扇形圆心角的度数.
23.(10分)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图(1)的位置时,
求证:①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图(3)的位置时,请直接写出DE,AD,BE之间的等量关系.
24.(12分)如图,在△ABC中,AB=50cm,BC=30cm,AC=40cm.
(1)求证:∠ACB=90°
(2)求AB边上的高.
(3)点D从点B出发在线段AB上以2cm/s的速度向终点A运动,设点D的运动时间为t(s).
①BD的长用含t的代数式表示为 .
②当△BCD为等腰三角形时,直接写出t的值.
2022-2023学年吉林省长春市榆树市八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(每小题3分,共24分)
1.(3分)四个数0,1,2,13中,无理数的是( )
A.2 B.1 C.13 D.0
【解答】解:A、2是无限不循环小数,是无理数,故此选项符合题意;
B、1是有理数,故此选项不符合题意;
C、13是分数,是有理数,故此选项不符合题意;
D、0是有理数,故此选项不符合题意.
故选:A.
2.(3分)下列运算中,正确的是( )
A.a6÷a2=a3 B.﹣a2•a4=a6 C.(ab)3=a3b3 D.(a2)4=a6
【解答】解:A、a6÷a2=a4,故此选项错误;
B、﹣a2•a4=﹣a6,故此选项错误;
C、(ab)3=a3b3,正确;
D、(a2)4=a8,故此选项错误;
故选:C.
3.(3分)小东5分钟内共投篮60次,共进球15个,则小东进球的频率是( )
A.0.25 B.60 C.0.26 D.15
【解答】解:∵小东5分钟内共投篮60次,共进球15个,
∴小东进球的频率是:1560=0.25.
故选:A.
4.(3分)下列各式从左到右的变形,属于因式分解的是( )
A.x2+2x+3=(x+1)2+2 B.(x+y)(x﹣y)=x2﹣y2
C.x2﹣xy+y2=(x﹣y)2+xy D.2x﹣2y=2(x﹣y)
【解答】解:A、x2+2x+3=(x+1)2+2,右边不是几个整式的积的形式,不属于因式分解,故此选项不符合题意;
B、(x+y)(x﹣y)=x2﹣y2,是整式的乘法,不属于因式分解,故此选项不符合题意;
C、x2﹣xy+y2=(x﹣y)2+xy,右边不是几个整式的积的形式,不属于因式分解,故此选项不符合题意;
D、3x2+2x=x(3x+2),右边是几个整式的积的形式,属于因式分解,故此选项符合题意.
故选:D.
5.(3分)如图所示,在△ABC中,∠ACB=90°,分别以AB、BC、AC为边向外作正方形,若三个正方形的面积分别为225、400、S,则S的值为( )
A.25 B.175 C.600 D.625
【解答】解:在△ABC中,∠ACB=90°,
由勾股定理得:AC2+BC2=AB2,
∴225+400=S,
∴S=625.
故选:D.
6.(3分)如图,若AB∥CD,AD=CD,∠1=70°,则∠2的度数是( )
A.70° B.40° C.35° D.20°
【解答】解:∵AB∥CD,∠1=70°,
∴∠ACD=∠1=70°.
∵AD=CD,
∴∠CAD=∠ACD=70°,
∴∠2=180°﹣∠ACD﹣∠CAD=180°﹣70°﹣70°=40°.
故选:B.
7.(3分)在△ABC中,∠BAC=90°,AB>AC,∠B≠30°,用无刻度的直尺和圆规在BC边上找一点D,使AD=BD,下列作法正确的是( )
A. B.
C. D.
【解答】解:若要在BC边上找一点D,使AD=BD,
则点D应该是线段AB垂直平分线与BC的交点,
故选:D.
8.(3分)如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC=( )
A.28° B.59° C.60° D.62°
【解答】解:∵在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,
∴△CAE≌△DAE,∴∠CAE=∠DAE=12∠CAB,
∵∠B+∠CAB=90°,∠B=28°,
∴∠CAB=90°﹣28°=62°,
∴∠AEC=90°-12∠CAB=90°﹣31°=59°.
故选:B.
二、填空题(每小题3分,共18分)
9.(3分)计算:x•x2= x3 .
【解答】解:原式=x3,
故答案为:x3.
10.(3分)分解因式:a2﹣4= (a+2)(a﹣2) .
【解答】解:a2﹣4=(a+2)(a﹣2).
11.(3分)命题“同旁内角互补,两直线平行”的逆命题是 两直线平行,同旁内角互补 .
【解答】解:命题“同旁内角互补,两直线平行”的逆命题是:两直线平行,同旁内角互补,
故答案为:两直线平行,同旁内角互补.
12.(3分)如图,在△ABC中,∠C=90°,AD平分∠BAC,若CD=2,AB=5,则△ABD的面积为 5 .
【解答】解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD=2,
∴△ABD的面积=12AB•DE=12×5×2=5.
故答案为:5.
13.(3分)某学校开展“我最喜欢的职业”为主题的调查,把随机调查200名学生得到的数据整理画出如图折线统计图(不完整).若选择教师人数与选择医生人数比为5:2,则选择医生的有 20 人.
【解答】解:由图可知公务员有40人,军人有20人,其他有70人,
∴教师和医生总共有200﹣40﹣20﹣70=70(人),
∵选择教师人数与选择医生人数比为5:2,
∴选择医生的有70×27=20(人).
故答案为:20.
14.(3分)如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠DAE=72°,则∠EDC的度数为 33° .
【解答】解:∵∠BAD=30°,∠DAE=72°,AB=AC,
∴∠B=∠C=180°-∠BAD+∠DAE2=39°,
∵AD=DE,
∴∠DAE=∠DEA=72°,
∵∠AED=∠C+∠EDC,
∴∠EDC=∠AED﹣∠C=72°﹣39°=33°,
故答案为:33°.
三、解答题(本大题共10小题,共78分)
15.(8分)计算:
(1)(2m2﹣m)2÷(﹣m2);
(2)(2x+5y)(3x﹣2y).
【解答】解:(1)(2m2﹣m)2÷(﹣m2)
=(4m4﹣4m3+m2)÷(﹣m2)
=﹣4m2+4m﹣1;
(2)(2x+5y)(3x﹣2y).
=6x2+15xy﹣4xy﹣10y2
=6x2+11xy﹣10y2.
16.(6分)因式分解:x2﹣4xy+4y2.
【解答】解:x2﹣4xy+4y2=(x﹣2y)2.
17.(7分)先化简,再求值:2(a+1)(a﹣1)﹣a(2a﹣3),其中a=-16.
【解答】解:原式=2(a2﹣1)﹣2a2+3a
=2a2﹣2﹣2a2+3a
=3a﹣2,
当a=-16时,
原式=3×(-16)﹣2
=-12-2
=-52.
18.(6分)图①、图②均是4×4的正方形网格,每个小正方形的顶点称为格点,小正方形的边长均为1,点A、点B均在格点上,在给定的网格中按要求画图,所画图形的顶点均在格点上.
(1)在图①中,以线段AB为腰画一个等腰三角形.
(2)在图②中,以线段AB为底画一个等腰三角形.
【解答】解:(1)如图1中,△ABC即为所求;
(2)如图2中,△ABC即为所求.
19.(6分)如图,△ABC中,AB=AC,DE垂直平分AC,若∠A=30°,求∠BCD的度数.
【解答】解:∵DE垂直平分AC,
∴DA=DC,
∴∠DCA=∠A=30°,
∵AB=AC,
∴∠B=∠ACB,
∵∠A+∠B+∠ACB=180°,
∴∠ACB=(180°﹣30°)÷2
=150°÷2
=75°,
∴∠BCD=∠ACB﹣∠DCA
=75°﹣30°
=45°.
∴∠BCD的度数为45°.
20.(8分)如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB.
(1)求修建的公路CD的长;
(2)若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?
【解答】解:(1)∵AC=15km,BC=20km,AB=25km,
152+202=252,
∴△ACB是直角三角形,∠ACB=90°,
∴CD=12AC×BC÷12÷AB=12(km).
故修建的公路CD的长是12km;
(2)在Rt△BDC中,BD=BC2-CD2=16(km),
一辆货车从C处经过D点到B处的路程=CD+BD=12+16=28(km).
故一辆货车从C处经过D点到B处的路程是28km.
21.(7分)如图,在△ABC中,AB=AC,AD是BC边上的中线,AE⊥BE于点E,且BE=12BC.求证:AB平分∠EAD.
【解答】证明:∵AB=AC,AD是BC边上的中线,
∴BD=12BC,AD⊥BC,
∵BE=12BC,
∴BD=BE,
∵AE⊥BE,
∴AB平分∠EAD.
22.(8分)某校数学兴趣小组为了解学生对A:新闻、B:体育、C:动画、D:娱乐、E:戏曲五类电视节目的喜爱情况,学校随机抽取了n名学生进行调查,规定每人必须并且只能在以上给出的五类中选择一类,并将统计结果绘制了两个不完整的统计图.
节目类型
人数
A
20
B
a
C
52
D
80
E
b
请根据图中所给出的信息解答下列问题:
(1)n= 200 ,a= 40 ,b= 8 .
(2)在扇形统计图中,求节目类型“C”所占的百分数.
(3)在扇形统计图中,求节目类型“D”所对应的扇形圆心角的度数.
【解答】解:(1)由统计表可知,喜爱A类节目的学生有20人,从扇形统计图中可得此部分占调查人数的10%,
本次抽样调查的学生总数n=20÷10%=200,
a=200×20%=40,
b=200﹣(20+40+52+80)=8.
故答案为:200,40,8;
(2)节目类型“C”所占的百分数是:52200×100%=26%;
(3)节目类型“D”所对应的扇形圆心角的度数是:360°×80200=144°.
23.(10分)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图(1)的位置时,
求证:①△ADC≌△CEB;
②DE=AD+BE;
(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图(3)的位置时,请直接写出DE,AD,BE之间的等量关系.
【解答】解:(1)①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠ACB=90°=∠CEB,
∴∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
∠CAD=∠BCE∠ADC=∠CEBAC=BC,
∴△ADC≌△CEB(AAS);
②∵△ADC≌△CEB,
∴CE=AD,CD=BE,
∴DE=CE+CD=AD+BE;
(2)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
∠CAD=∠BCE∠ADC=∠CEBAC=BC,
∴△ADC≌△CEB(AAS);
∴CE=AD,CD=BE,
∴DE=CE﹣CD=AD﹣BE;
(3)当MN旋转到题图(3)的位置时,AD,DE,BE所满足的等量关系是:DE=BE﹣AD.
理由如下:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°,
∴∠CAD=∠BCE,
∵在△ADC和△CEB中,
∠CAD=∠BCE∠ADC=∠CEBAC=BC,
∴△ADC≌△CEB(AAS),
∴CE=AD,CD=BE,
∴DE=CD﹣CE=BE﹣AD.
24.(12分)如图,在△ABC中,AB=50cm,BC=30cm,AC=40cm.
(1)求证:∠ACB=90°
(2)求AB边上的高.
(3)点D从点B出发在线段AB上以2cm/s的速度向终点A运动,设点D的运动时间为t(s).
①BD的长用含t的代数式表示为 2t .
②当△BCD为等腰三角形时,直接写出t的值.
【解答】证明:(1)∵BC2+AC2=900+1600=2500cm2,AB2=2500cm2,
∴BC2+AC2=AB2,
∴∠ACB=90°,
∴△ABC是直角三角形;
(2)设AB边上的高为hcm,
由题意得S△ABC=50⋅h2=30×402,
解得h=24.
∴AB边上的高为24cm;
(3)①∵点D从点B出发在线段AB上以2cm/s的速度向终点A运动,
∴BD=2t;
故答案为:2t;
②如图1,若BC=BD=30cm,则t=302=15s,
如图2,若CD=BC,过点C作CE⊥AB,
由(2)可知:CE=24cm,
∴BE=BC2-CE2=900-576=18cm,
∵CD=BC,且CE⊥BA,
∴DE=BE=18cm,
∴BD=36cm,
∴t=362=18s,
若CD=DB,如图2,
∵CD2=CE2+DE2,
∴CD2=(CD﹣18)2+576,
∴CD=25,
∴t=252s,
综上所述:当t=15s或18s或252s时,△BCD为等腰三角形.
吉林省长春市榆树市2023-2024学年八年级上学期期末数学试卷+: 这是一份吉林省长春市榆树市2023-2024学年八年级上学期期末数学试卷+,共16页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
吉林省长春市榆树市2022-2023学年七年级上学期期末数学试卷(含答案): 这是一份吉林省长春市榆树市2022-2023学年七年级上学期期末数学试卷(含答案),共17页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
吉林省长春市榆树市2022-2023学年七年级上学期期末数学试卷: 这是一份吉林省长春市榆树市2022-2023学年七年级上学期期末数学试卷,共15页。












