河南省信阳市光山县2022-2023学年九年级上学期期末数学试卷(含答案)

这是一份河南省信阳市光山县2022-2023学年九年级上学期期末数学试卷(含答案)，共28页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年河南省信阳市光山县九年级（上）期末数学试卷
一、选择题（本大题共10小题，共30分。在每小题列出的选项中，选出符合题目的一项）
1．（3分）为推动世界冰雪运动的发展，我国于2022年2月2日至20日举办了北京冬奥会、如图是冬奥会会标征集活动中的部分参选作品，其文字上方的图案既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
2．（3分）若x＝1是关于x的一元二次方程x2﹣mx+3＝0的一个解，则m的值是（　　）
A．6 B．5 C．4 D．3
3．（3分）如图，△COD是△AOB绕点O顺时针方向旋转30°后所得的图形，点C恰好在AB上，则∠A的度数为（　　）

A．30° B．60° C．70° D．75°
4．（3分）若A（﹣2，y1），B（﹣1，y2），C（2，y3）为二次函数＝x2+2x+2的图象上的三点，则y1，y2，y3的大小关系
是（　　）
A．y1＜y2＜y3 B．y1＜y3＜y2 C．y2＜y1＜y3 D．y3＜y1＜y2
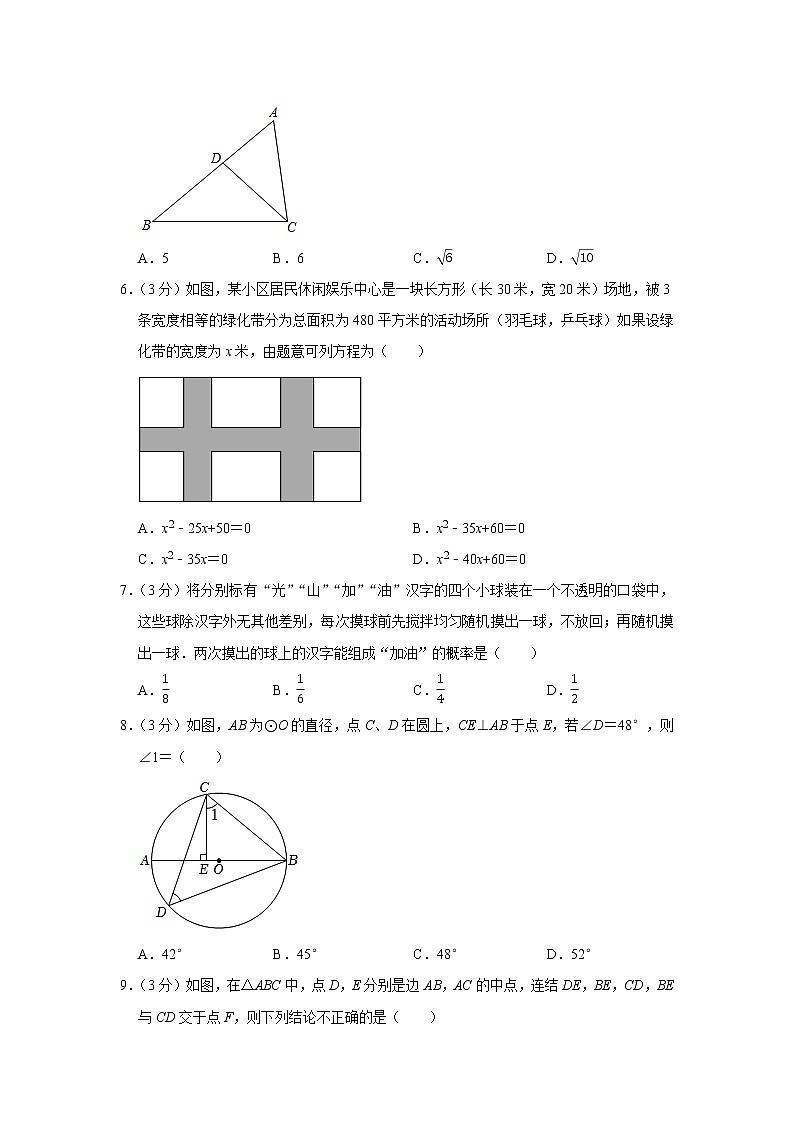
5．（3分）如图，在△ABC中，点D在AB上，∠ACD＝∠B．若AD＝2，BD＝3，则AC等于
（　　）

A．5 B．6 C．6 D．10
6．（3分）如图，某小区居民休闲娱乐中心是一块长方形（长30米，宽20米）场地，被3条宽度相等的绿化带分为总面积为480平方米的活动场所（羽毛球，乒乓球）如果设绿化带的宽度为x米，由题意可列方程为（　　）

A．x2﹣25x+50＝0 B．x2﹣35x+60＝0
C．x2﹣35x＝0 D．x2﹣40x+60＝0
7．（3分）将分别标有“光”“山”“加”“油”汉字的四个小球装在一个不透明的口袋中，这些球除汉字外无其他差别，每次摸球前先搅拌均匀随机摸出一球，不放回；再随机摸出一球．两次摸出的球上的汉字能组成“加油”的概率是（　　）
A．18 B．16 C．14 D．12
8．（3分）如图，AB为⊙O的直径，点C、D在圆上，CE⊥AB于点E，若∠D＝48°，则∠1＝（　　）

A．42° B．45° C．48° D．52°
9．（3分）如图，在△ABC中，点D，E分别是边AB，AC的中点，连结DE，BE，CD，BE与CD交于点F，则下列结论不正确的是（　　）

A．BC＝2DE B．BE＝3EF
C．S△ABC＝4S△ADE D．AB＝2AE
10．（3分）如图，在矩形ABCD中，AB＝2cm，BC＝43cm，E是AD的中点，连接BE，CE．点P从点B出发，以3cm/s的速度沿BC方向运动到点C停止，同时点Q从点B出发，以1cm/s的速度沿BE﹣EC方向运动到点C停止，若△BPQ的面积为y（cm2），运动时间为x（s），则下列最能反映y与x之间函数关系的图象是（　　）

A． B．
C． D．
二、填空题（本大题共5小题，共15分）
11．（3分）已知点P（2，﹣3）与点Q（a，b）关于原点对称，则a+b＝　 　．
12．（3分）一个正六边形外接圆的半径等于2cm，则这个正六边形的周长等于 　 　cm．
13．（3分）如图，A是反比例函数图象上一点，过点A作AB⊥y轴于点B，点P在x轴上，OP＝AB，四边形ABPO的面积为6，则这个反比例函数的表达式为 　 　．

14．（3分）如图，在扇形ABC中，∠BAC＝90°，AB＝1，若以点C为圆心，CA为半径画弧，与BC交于点D，则图中阴影部分的面积和是 　 　．

15．（3分）如图，在Rt△ABC中，∠C＝90°，∠A＝30°，AB＝8，点D是边AB的中点，点P是边BC上一动点，连接PD，将线段PD绕点P顺时针旋转，使点D的对应点D′落在边AC上，连接DD'，若△ADD'为直角三角形，则BP的长为　 　．

三、解答题（本大题共9小题，共75分。解答应写出文字说明，证明过程或演算步骤）
16．计算：14-（﹣2）﹣1+（2-2）0．
17．化简（1-1x-1）÷x2-4x+4x2-1．
18．已知关于x的一元二次方程x2﹣2（m+1）x+m2﹣3＝0有两个不相等的实数根．
（1）求实数m的取值范围；
（2）求出满足m的取值范围的最小整数值m，并求出此时方程的两根．
19．2020年6月26日是第33个国际禁毒日，为了解同学们对禁毒知识的掌握情况，从广安市某校800名学生中随机抽取部分学生进行调查，调查分为“不了解”“了解较少”“比较了解”“非常了解”四类，并根据调查结果绘制出如图所示的两幅不完整的统计图．请根据统计图回答下列问题：
（1）本次抽取调查的学生共有　 　人，估计该校800名学生中“比较了解”的学生有　 　人．
（2）请补全条形统计图．
（3）“不了解”的4人中有3名男生A1，A2，A3，1名女生B，为了提高学生对禁毒知识的了解，对这4人进行了培训，然后随机抽取2人对禁毒知识的掌握情况进行检测，请用画树状图或列表的方法，求恰好抽到2名男生的概率．

20．如图，AB是⊙O的直径，射线BC交⊙O于点D，E是劣弧AD上一点，且AE=DE，过点E作EF⊥BC于点F，延长FE和BA的延长线交于点G．
（1）证明：GF是⊙O的切线；
（2）若AG＝6，GE＝62，求△GOE的面积．

21．已知A（﹣4，2），B（n，﹣4）两点是一次函数y＝kx+b和反比例函数y=mx图象的两个交点．
（1）求一次函数和反比例函数的解析式；
（2）求△AOB的面积；
（3）观察图象，直接写出不等式kx+b-mx＞0的解集．

22．某片果园有果树80棵，现准备多种一些果树提高果园产量，但是如果多种树，那么树之间的距离和每棵树所受光照就会减少，单棵树的产量随之降低．若该果园每棵果树产果y（千克），增种果树x（棵），它们之间的函数关系如图所示．
（1）求y与x之间的函数关系式．
（2）在投入成本最低的情况下，增种果树多少棵时，果园可以收获果实7000千克．
（3）当增种果树多少棵时，果园的总产量w（千克）最大？此时每棵果树的产量是多少？

23．已知，抛物线y＝x2+bx+c交x轴于C，D两点，交y轴于点E，其中点C的坐标为（﹣1，0），对称轴为x＝1．点A，B为坐标平面内两点，其坐标为A（12，﹣5），B（4，﹣5）．
（1）求抛物线的解析式及顶点坐标；
（2）当﹣1≤x≤2时，求y的取值范围；
（3）连接AB，若抛物线y＝x2+bx+c向下平移k（k＞0）个单位时，与线段AB只有一个公共点，结合函数图象，直接写出k的取值范围．

24．如图，已知△ABC和△ADE均为等腰三角形，AC＝BC，DE＝AE，将这两个三角形放置在一起．
（1）问题发现
如图①，当∠ACB＝∠AED＝60°时，点B、D、E在同一直线上，连接CE，则∠CEB的度数为　 　，线段AE、BE、CE之间的数量关系是　 　；
（2）拓展探究
如图②，当∠ACB＝∠AED＝90°时，点B、D、E在同一直线上，连接CE．请判断∠CEB的度数及线段AE、BE、CE之间的数量关系，并说明理由；
（3）解决问题
如图③，∠ACB＝∠AED＝90°，AC＝25，AE＝2，连接CE、BD，在△AED绕点A旋转的过程中，当DE⊥BD时，请直接写出EC的长．


2022-2023学年河南省信阳市光山县九年级（上）期末数学试卷
参考答案与试题解析
一、选择题（本大题共10小题，共30分。在每小题列出的选项中，选出符合题目的一项）
1．（3分）为推动世界冰雪运动的发展，我国于2022年2月2日至20日举办了北京冬奥会、如图是冬奥会会标征集活动中的部分参选作品，其文字上方的图案既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
【解答】解：A．该图形既是轴对称图形，又是中心对称图形，故此选项符合题意；
B．该图形是轴对称图形，不是中心对称图形，故此选项不合题意；
C．该图形既不是轴对称图形，也不是中心对称图形，故此选项不合题意；
D．该图形是轴对称图形，不是中心对称图形，故此选项不合题意．
故选：A．
2．（3分）若x＝1是关于x的一元二次方程x2﹣mx+3＝0的一个解，则m的值是（　　）
A．6 B．5 C．4 D．3
【解答】解：∵x＝1是关于x的一元二次方程x2﹣mx+3＝0的一个解，
∴1﹣m+3＝0，
解得m＝4．
故选：C．
3．（3分）如图，△COD是△AOB绕点O顺时针方向旋转30°后所得的图形，点C恰好在AB上，则∠A的度数为（　　）

A．30° B．60° C．70° D．75°
【解答】解：∵△COD是△AOB绕点O顺时针方向旋转30°后所得的图形，
∴AO＝CO，∠AOC＝30°，
∴∠A＝∠ACO=180°-30°2=75°，
故选：D．
4．（3分）若A（﹣2，y1），B（﹣1，y2），C（2，y3）为二次函数＝x2+2x+2的图象上的三点，则y1，y2，y3的大小关系
是（　　）
A．y1＜y2＜y3 B．y1＜y3＜y2 C．y2＜y1＜y3 D．y3＜y1＜y2
【解答】解：∵对称轴为直线x=--22×1=-1，
且a＝1＞0，
∴A到对称轴直线x＝﹣1的距离为1，
B到对称轴直线x＝﹣1的距离为0，
C到对称轴直线x＝﹣1的距离为3，
∵0＜1＜3，
根据抛物线开口向上，离对称轴越近，函数值越小，
∴y2＜y1＜y3．
故选：C．
5．（3分）如图，在△ABC中，点D在AB上，∠ACD＝∠B．若AD＝2，BD＝3，则AC等于
（　　）

A．5 B．6 C．6 D．10
【解答】解：在△ADC和△ACB中，
∵∠ACD＝∠B，∠A＝∠A，
∴△ADC∽△ACB，
∴AC：AB＝AD：AC，
∴AC2＝AB•AD，
∵AD＝2，AB＝AD+BD＝2+3＝5，
∴AC2＝5×2＝10，
∵AC＞0，
∴AC=10，
故选：D．
6．（3分）如图，某小区居民休闲娱乐中心是一块长方形（长30米，宽20米）场地，被3条宽度相等的绿化带分为总面积为480平方米的活动场所（羽毛球，乒乓球）如果设绿化带的宽度为x米，由题意可列方程为（　　）

A．x2﹣25x+50＝0 B．x2﹣35x+60＝0
C．x2﹣35x＝0 D．x2﹣40x+60＝0
【解答】解：根据题意得，绿化带的长和宽就应该分别为（20﹣x）m和（30﹣2x）m，
所以方程为（20﹣x）（30﹣2x）＝480，
x2﹣35x+60＝0，
故选：B．
7．（3分）将分别标有“光”“山”“加”“油”汉字的四个小球装在一个不透明的口袋中，这些球除汉字外无其他差别，每次摸球前先搅拌均匀随机摸出一球，不放回；再随机摸出一球．两次摸出的球上的汉字能组成“加油”的概率是（　　）
A．18 B．16 C．14 D．12
【解答】解：列表如下：
　
光
山
加
油
光

（山，郑）
（加，光）
（油，光）
山
（光，山）

（加，山）
（油，山）
加
（光，加）
（山，加）

（油，加）
油
（光，油）
（山，油）
（加，油）

由树状图知，共有12种等可能结果，其中两次摸出的球上的汉字能组成“加油”的有2种结果，
∴两次摸出的球上的汉字能组成“加油”的概率为212=16．
故选：B．
8．（3分）如图，AB为⊙O的直径，点C、D在圆上，CE⊥AB于点E，若∠D＝48°，则∠1＝（　　）

A．42° B．45° C．48° D．52°
【解答】解：连接AC，

由圆周角定理得：∠A＝∠D，
∵∠D＝48°，
∴∠A＝48°，
∵AB是⊙O的直径，
∴∠ACB＝90°，
∴∠ABC＝90°﹣∠A＝42°，
∵CE⊥AB，
∴∠BEC＝90°，
∴∠1＝90°﹣∠ABC＝48°，
故选：C．
9．（3分）如图，在△ABC中，点D，E分别是边AB，AC的中点，连结DE，BE，CD，BE与CD交于点F，则下列结论不正确的是（　　）

A．BC＝2DE B．BE＝3EF
C．S△ABC＝4S△ADE D．AB＝2AE
【解答】解：A．∵点D，E分别是边AB，AC的中点，
∴BC＝2DE，
故选项正确；
B．∵点D，E分别是边AB，AC的中点，
∴BC＝2DE，DE∥BC，
∴△BCF∽△EDF，
∴BCDE=BFEF=2，
∴BE＝3EF，
故选项正确；
C．∵DE∥BC，
∴△ABC∽△ADE，
∴S△ABCS△ADE=(BCDE)2=4，
∴S△ABC＝4S△ADE，
故选项正确；
D．∵E是AC的中点，
∴AC＝2AE，
当AB≠AC时，AB≠2AE，
故选项错误；
故选：D．
10．（3分）如图，在矩形ABCD中，AB＝2cm，BC＝43cm，E是AD的中点，连接BE，CE．点P从点B出发，以3cm/s的速度沿BC方向运动到点C停止，同时点Q从点B出发，以1cm/s的速度沿BE﹣EC方向运动到点C停止，若△BPQ的面积为y（cm2），运动时间为x（s），则下列最能反映y与x之间函数关系的图象是（　　）

A． B．
C． D．
【解答】解：在矩形ABCD中，AB＝2cm，BC＝43cm，
∴DC＝AB＝2cm，AD＝BC＝43cm，
∵E是AD的中点，
∴AE＝DE＝23cm，
由勾股定理可得，BE＝CE＝4cm，
∴∠AEB＝30°，
∴∠EBC＝∠AEB＝30°．
由点P，Q的运动可知，点Q从点B到点E用时4s，从点E到点C用时4s，点P从点B到点C用时4s，
∴点Q到达点E时，点P运动到点C处，
由此可知分两段：
①当0＜t＜4时，如图，过点Q作QM⊥BC于点M，

∴BQ＝t，BP=3t，
∵∠EBC＝30°，
∴QM=12t，
∴y=12•BP•QM=12⋅3t⋅12t=34t2，此段图象为抛物线，且开口向上，由此排除A，C；
②当4＜t＜8时，如图，此时点Q在EC上，过点Q作QN⊥BC于点N，

由点Q的运动可知，CQ＝8﹣t，
∵∠BCE＝30°，
∴QN=12（8﹣4），
∴y==12•BC•QN=12×43•12（8﹣t）=-3t+83，此段图象为直线的一部分，由此排除B；
故选：D．

二、填空题（本大题共5小题，共15分）
11．（3分）已知点P（2，﹣3）与点Q（a，b）关于原点对称，则a+b＝　1　．
【解答】解：由点P（2，﹣3）与点Q（a，b）关于原点对称，得
a＝﹣2，b＝3，
则a+b＝﹣2+3＝1，
故答案为：1．
12．（3分）一个正六边形外接圆的半径等于2cm，则这个正六边形的周长等于 　12　cm．
【解答】解：∵正六边形外接圆的半径等于边长，
∴正六边形的边长＝2cm，
正六边形的周长＝6×2＝12（cm），
故答案为：12．
13．（3分）如图，A是反比例函数图象上一点，过点A作AB⊥y轴于点B，点P在x轴上，OP＝AB，四边形ABPO的面积为6，则这个反比例函数的表达式为 　y=-6x　．

【解答】解：设反比例函数的解析式为y=kx，
∵AB⊥y轴于点B，
∴AB∥OP，
∵OP＝AB，
∴四边形AOPB是平行四边形，
∴△AOB的面积=12四边形ABPO的面积=12|k|，
∴|k|＝6，
∴k＝±6；
又∵反比例函数的图象的一支位于第二象限，
∴k＜0．
∴k＝﹣6．
∴这个反比例函数的解析式为y=-6x．
故答案为：y=-6x．
14．（3分）如图，在扇形ABC中，∠BAC＝90°，AB＝1，若以点C为圆心，CA为半径画弧，与BC交于点D，则图中阴影部分的面积和是 　112π　．

【解答】解：连接AD，

∵以点C为圆心，CA为半径画弧，与BC交于点D，AB＝1，
∴AD＝AC＝CD＝1，
∴△ADC是等边三角形，
∴∠DCA＝∠DAC＝60°，
∵∠BAC＝90°，
∴∠BAD＝∠BAC﹣∠DAC＝90°﹣60°＝30°，
∴阴影部分的面积＝S扇形BAD=30⋅π×12360=112π，
故答案为：112π．
15．（3分）如图，在Rt△ABC中，∠C＝90°，∠A＝30°，AB＝8，点D是边AB的中点，点P是边BC上一动点，连接PD，将线段PD绕点P顺时针旋转，使点D的对应点D′落在边AC上，连接DD'，若△ADD'为直角三角形，则BP的长为　3或43　．

【解答】解：∵∠C＝90°，∠A＝30°，AB＝8，
∴BC＝4，
∵点D是边AB的中点，
∴AD＝BD＝4，
如图，当∠AD'D＝90°时，过点P作PH⊥DD'于H，

∵∠A＝30°，
∴DD'=12AD＝2，
∵将线段PD绕点P顺时针旋转，使点D的对应点D′落在边AC上，
∴DP＝D'P，
∵PH⊥DD'，
∴D'H＝DH＝1，
∵∠C＝∠PHD'＝∠CD'H＝90°，
∴四边形PCD'H是矩形，
∴CP＝D'H＝1，
∴BP＝3，
如图，当∠ADD'＝90°时，过点P作PH⊥DD'于H，PG⊥DB于G，

∵∠A＝30°，
∴DD'=433，
∵将线段PD绕点P顺时针旋转，使点D的对应点D′落在边AC上，
∴DP＝D'P，
∵PH⊥DD'，
∴D'H＝DH=233，
∵∠PGD＝∠PHD＝∠BDH＝90°，
∴四边形PHDG是矩形，
∴HD＝PG=233，
∵∠B＝60°，
∴sinB=PGPB=32，
∴PB=43，
故答案为：3或43．
三、解答题（本大题共9小题，共75分。解答应写出文字说明，证明过程或演算步骤）
16．计算：14-（﹣2）﹣1+（2-2）0．
【解答】解：14-（﹣2）﹣1+（2-2）0
=12-1-2+1
=12+12+1
＝2．
17．化简（1-1x-1）÷x2-4x+4x2-1．
【解答】解：（1-1x-1）÷x2-4x+4x2-1
=x-2x-1÷(x-2)2(x+1)(x-1)
=x-2x-1•(x+1)(x-1)(x-2)2
=x+1x-2．
18．已知关于x的一元二次方程x2﹣2（m+1）x+m2﹣3＝0有两个不相等的实数根．
（1）求实数m的取值范围；
（2）求出满足m的取值范围的最小整数值m，并求出此时方程的两根．
【解答】解：（1）∵关于x的一元二次方程x2﹣2（m+1）x+m2﹣3＝0有两个不相等的实数根，
∴Δ＝[﹣2（m+1）]2﹣4×1×（m2﹣3）＝8m+16＞0，
解得：m＞﹣2；
（2）∵满足m＞﹣2的最小整数是﹣1，
∴m＝﹣1，
把m＝﹣1代入方程得：x2﹣2＝0，
解得：x1=2，x2=-2．
19．2020年6月26日是第33个国际禁毒日，为了解同学们对禁毒知识的掌握情况，从广安市某校800名学生中随机抽取部分学生进行调查，调查分为“不了解”“了解较少”“比较了解”“非常了解”四类，并根据调查结果绘制出如图所示的两幅不完整的统计图．请根据统计图回答下列问题：
（1）本次抽取调查的学生共有　40　人，估计该校800名学生中“比较了解”的学生有　320　人．
（2）请补全条形统计图．
（3）“不了解”的4人中有3名男生A1，A2，A3，1名女生B，为了提高学生对禁毒知识的了解，对这4人进行了培训，然后随机抽取2人对禁毒知识的掌握情况进行检测，请用画树状图或列表的方法，求恰好抽到2名男生的概率．

【解答】解：（1）本次调查的学生总人数为4÷10%＝40（人）；
∵本次抽取调查的学生中，“比较了解”的学生有：40﹣14﹣6﹣4＝16（人），
∴估计该校800名学生中“比较了解”的学生有800×1640=320（人），
故答案为：40，320；
（2）补全条形统计图如图：

（3）画树状图如图：

共有12个等可能的结果，恰好抽到2名男生的结果有6个，
∴恰好抽到2名男生的概率为612=12．
20．如图，AB是⊙O的直径，射线BC交⊙O于点D，E是劣弧AD上一点，且AE=DE，过点E作EF⊥BC于点F，延长FE和BA的延长线交于点G．
（1）证明：GF是⊙O的切线；
（2）若AG＝6，GE＝62，求△GOE的面积．

【解答】解：（1）如图，连接OE，

∵AE=DE，
∴∠1＝∠2，
∵∠2＝∠3，
∴∠1＝∠3，
∴OE∥BF，
∵BF⊥GF，
∴OE⊥GF，
∴GF是⊙O的切线；

（2）设OA＝OE＝r，
在Rt△GOE中，∵AG＝6，GE＝62，
∴由OG2＝GE2+OE2可得（6+r）2＝（62）2+r2，
解得：r＝3，
即OE＝3，
则S△GOE=12•OE•GE=12×3×62=92．
21．已知A（﹣4，2），B（n，﹣4）两点是一次函数y＝kx+b和反比例函数y=mx图象的两个交点．
（1）求一次函数和反比例函数的解析式；
（2）求△AOB的面积；
（3）观察图象，直接写出不等式kx+b-mx＞0的解集．

【解答】解：（1）把A（﹣4，2）代入y=mx，
得m＝2×（﹣4）＝﹣8，则反比例函数解析式为y=-8x．
把B（n，﹣4）代入y=-8x，
得﹣4n＝﹣8，解得n＝2，则B点坐标为（2，﹣4）．
把A（﹣4，2）、B（2，﹣4）代入y＝kx+b得
-4k+b=22k+b=-4，
解得k=-1b=-2，
则一次函数解析式为y＝﹣x﹣2．
（2）直线与x轴的交点为C，在y＝﹣x﹣2中，令y＝0，则x＝﹣2，
即直线y＝﹣x﹣2与x轴交于点C（﹣2，0），
∴OC＝2．
∴S△AOB＝S△AOC+S△BOC=12×2×2+12×2×4＝6．
（3）由图可得，不等式kx+b-mx＞0解集范围是x＜﹣4或0＜x＜2．
22．某片果园有果树80棵，现准备多种一些果树提高果园产量，但是如果多种树，那么树之间的距离和每棵树所受光照就会减少，单棵树的产量随之降低．若该果园每棵果树产果y（千克），增种果树x（棵），它们之间的函数关系如图所示．
（1）求y与x之间的函数关系式．
（2）在投入成本最低的情况下，增种果树多少棵时，果园可以收获果实7000千克．
（3）当增种果树多少棵时，果园的总产量w（千克）最大？此时每棵果树的产量是多少？

【解答】解：（1）根据题中的图可以看出，y与x为一次函数的关系，
设函数关系式为y＝kx+b，将（12，74）、（28，66）代入关系式可得
12k+b=7428k+b=66解得k=-12，b＝80，
所以y与x之间的函数关系式为y=-12x+80．
（2）根据题意可列方程(-12x+80)(x+80)=7000，
化简得x2﹣80x+1200＝0，解得x1＝20，x2＝60，
因为题中要求投入成本最低的情况下，所以x2＝60不符题意舍去，
答：增种果树20棵时，果园可以收获果实7000千克．
（3）根据题意可列函数关系式w＝（-12x+80）（x+80）=-12（x﹣40）2+7200．
令y≥0，可求出自变量x的取值范围是0≤x≤160，
所以当x＝40时，w可取到最大值7200，每颗果树的产量为y=-12x+80＝60
答：当增种果树40棵时，果园的总产量最大．每颗果树的产量为60千克．
23．已知，抛物线y＝x2+bx+c交x轴于C，D两点，交y轴于点E，其中点C的坐标为（﹣1，0），对称轴为x＝1．点A，B为坐标平面内两点，其坐标为A（12，﹣5），B（4，﹣5）．
（1）求抛物线的解析式及顶点坐标；
（2）当﹣1≤x≤2时，求y的取值范围；
（3）连接AB，若抛物线y＝x2+bx+c向下平移k（k＞0）个单位时，与线段AB只有一个公共点，结合函数图象，直接写出k的取值范围．

【解答】解：（1）∵抛物线对称轴为直线x=-b2=1，
∴b＝﹣2，
∴y＝x2﹣2x+c，
将（﹣1，0）代入y＝x2﹣2x+c得0＝1+2+c，
解得c＝﹣3，
∴y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
∴抛物线顶点坐标为（1，﹣4）．
（2）∵y＝（x﹣1）2﹣4，
∴x＝1时，y取最小值为4，
∵1﹣（﹣1）＞2﹣1，
∴x＝﹣1时，y＝0为最大值，
∴当﹣1≤x≤2时，﹣4≤y≤0．
（3）抛物线y＝（x﹣1）2﹣4向下平移k个单位后解析式为y＝（x﹣1）2﹣4﹣k，
∴抛物线顶点坐标为（1，﹣4﹣k），
①当抛物线顶点落在AB上时，﹣4﹣k＝﹣5，
解得k＝1，
②当抛物线经过点A（12，﹣5）时，﹣5＝（12）2﹣4﹣k，
解得k=54，
当抛物线经过B（4，﹣5）时，﹣5＝32﹣4﹣k，
解得k＝10，
∴54＜k≤10时，满足题意．
综上所述，k＝1或54＜k≤10．
24．如图，已知△ABC和△ADE均为等腰三角形，AC＝BC，DE＝AE，将这两个三角形放置在一起．
（1）问题发现
如图①，当∠ACB＝∠AED＝60°时，点B、D、E在同一直线上，连接CE，则∠CEB的度数为　60°　，线段AE、BE、CE之间的数量关系是　BE＝AE+CE　；
（2）拓展探究
如图②，当∠ACB＝∠AED＝90°时，点B、D、E在同一直线上，连接CE．请判断∠CEB的度数及线段AE、BE、CE之间的数量关系，并说明理由；
（3）解决问题
如图③，∠ACB＝∠AED＝90°，AC＝25，AE＝2，连接CE、BD，在△AED绕点A旋转的过程中，当DE⊥BD时，请直接写出EC的长．

【解答】解：（1）在△ABC为等腰三角形，AC＝BC，∠ACB＝60°，
∴△ABC是等边三角形，
∴AC＝AB，∠CAB＝60°，
同理：AE＝AD，∠AED＝∠ADE＝∠EAD＝60°，
∴∠EAD＝∠CAB，
∴∠EAC＝∠DAB，
∴△ACE≌△ABD（SAS），
∴CE＝BD，∠AEC＝∠ADB，
∵点B、D、E在同一直线上，
∴∠ADB＝180°﹣∠ADE＝120°，
∴∠AEC＝120°，
∴∠CEB＝∠AEC﹣∠AEB＝60°，
∵DE＝AE，
∴BE＝DE+BD＝AE+CE，
故答案为60°，BE＝AE+CE；
（2）在等腰三角形ABC中，AC＝BC，∠ACB＝90°，
∴AB=2AC，∠CAB＝45°，
同理，AD=2AE，∠AED＝90°，∠ADE＝∠DAE＝45°，
∴AEAD=ACAB，∠DAE＝∠CAB，
∴∠EAC＝∠DAB，
∴△ACE∽△ABD，
∴BDCE=ADAE=2，
∴∠AEC＝∠ADB，BD=2CE，
∵点B、D、E在同一条直线上，
∴∠ADB＝180°﹣∠ADE＝135°，
∴∠AEC＝135°，
∴∠CEB＝∠AEC﹣∠AED＝45°，
∵DE＝AE，
∴BE＝DE+BD＝AE+2CE；

（3）由（2）知，△ACE∽△ABD，
∴BD=2CE，
在Rt△ABC中，AC＝25，
∴AB=2AC＝210，
①当点E在点D上方时，如图③，
过点A作AP⊥BD交BD的延长线于P，
∵DE⊥BD，
∴∠PDE＝∠AED＝∠APD，
∴四边形APDE是矩形，
∵AE＝DE，
∴矩形APDE是正方形，
∴AP＝DP＝AE＝2，
在Rt△APB中，根据勾股定理得，BP=AB2-AP2=6，
∴BD＝BP﹣AP＝4，
∴CE=12BD＝22；
②当点E在点D下方时，如图④
同①的方法得，AP＝DP＝AE＝2，BP＝6，
∴BD＝BP+DP＝8，
∴CE=12BD＝42，
即：CE的长为22或42．