初中数学人教版九年级下册27.2.3 相似三角形应用举例学案

这是一份初中数学人教版九年级下册27.2.3 相似三角形应用举例学案，共9页。
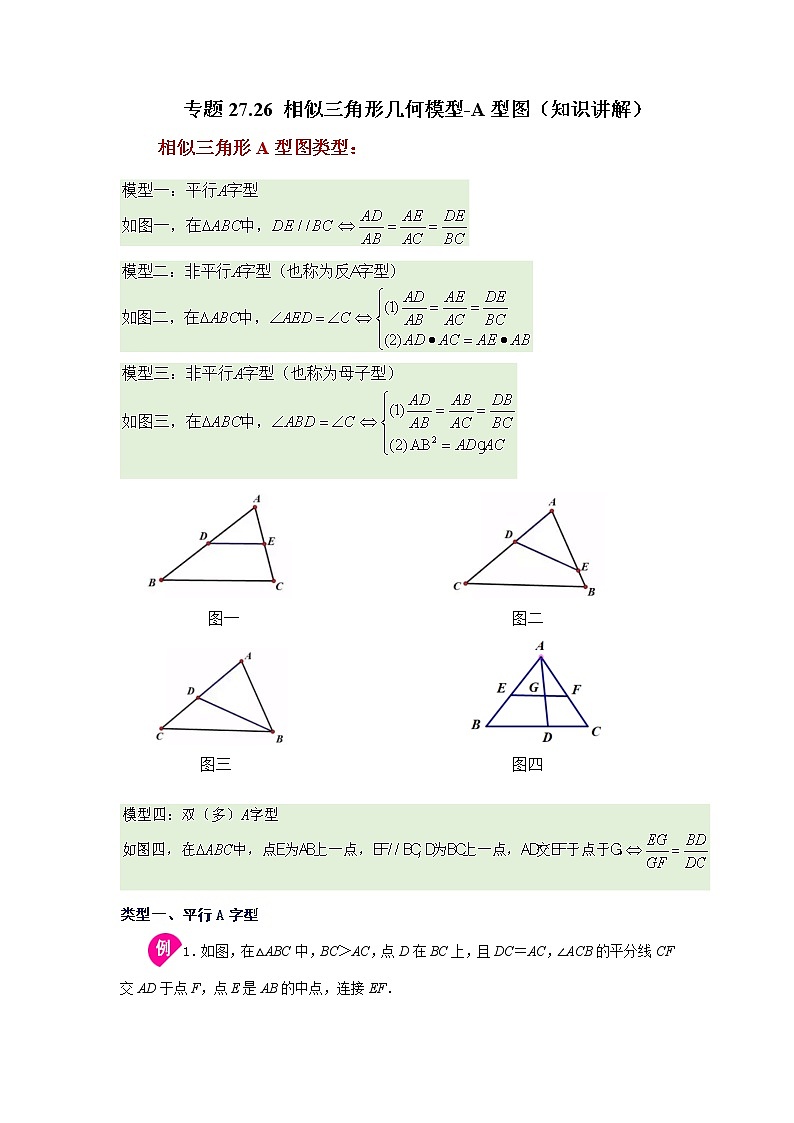
专题27.26 相似三角形几何模型-A型图（知识讲解）相似三角形A型图类型：                             图一                                  图二                                图三                                   图四            类型一、平行A字型1．如图，在△ABC中，BC＞AC，点D在BC上，且DC＝AC，∠ACB的平分线CF交AD于点F，点E是AB的中点，连接EF．(1)  求证：△AEF∽△ABD；(2)  填空：① 若BC＝8，AC＝5，则EF＝_________；② 若四边形BDFE的面积为6，则△ABD的面积为_________ ．【答案】(1)见分析   (2)  ①；②  8【分析】（1）首先判定△ADC是等腰三角形，然后利用等腰三角形的性质得到点F是AD的中点，然后得到EF是△ABD的中位线，进而可证明△AEF∽△ABD；（2）①因为EF是△ABD的中位线，所以BD=2EF，求出BD的长即可得到EF的长；②根据（1）证得的平行可以判定△AEF∽ABD，然后利用相似三角形面积的比等于相似比的平方求的△ABD的面积．（1）证明：∵CF平分∠ACB，∴∠ACF=∠BCF，又∵DC=AC，∴CF是△ACD的中线，∴点F是AD的中点，又∵E是AB的中点，∴EF是△ABD的中位线，∴EF∥BD，∴△AEF∽△ABD；（2）解：①∵EF是△ABD的中位线，∴EF=BD，∵BC=8，AC=5，DC=AC，∴BD=BC-CD=3，∴EF=1.5，故答案为1.5；②∵△AEF∽△ABD，∴S△AEF：S△ABD=1：4，∴S△AEF：S四边形BDFE=1：3，∵四边形BDFE的面积为6，∴S△AEF=2，∴S△ABD=S△AEF+S四边形BDFE=2+6=8，故答案为：8．【点拨】本题主要考查等腰三角形的判定和性质、三角形中位线的定义和性质、相似三角形的判定和性质，解题的关键在于求证EF为中位线，S△AEF：S△ABD=1：4．举一反三【变式1】如图，点D，E 在BC 上，且,求证：      【分析】利用平行关系，找出对应角相等，即可证明相似．证明：∵，∴，∵，∴，在和中， ，，∴．【点拨】本题考查相似三角形的判定，解题关键找到需要的条件．【变式2】如图，在△ABC中，点D、E、F分别在AB、BC、AC边上，DE∥AC，∠DEF＝∠A．求证：△BDE∽△EFC．     【分析】根据，得出，根据可判断，可证．证明：，，又，，，，．【点拨】本题考查平行线性质，三角形相似判定，掌握平行线性质，三角形相似判定是解题关键．类型二、非平行A字型（反A字型）2．已知：D、E是△ABC的边AB、AC上的点，AB＝8，AD＝3，AC＝6，AE＝4，求证：△ABC∽△AED．  【分析】根据已知线段长度求出，再根据∠A=∠A推出相似即可．证明：在△ABC和△AED 中，∵，，∴，又∵∠A＝∠A， ∴△ABC∽△AED．【点拨】本题考查了相似三角形的判定定理的应用，注意：有两边的对应成比例，且夹角相等的两三角形相似．举一反三【变式1】如图，在中，、分别是、边上的高．求证：．  【分析】要证明，这两个三角形已经有一个公共角相等，此时可以考虑用两组对应边的比相等且相应的夹角相等的两个三角形相似，即找到CD：CA与CE：CB是否相等，这时不能直接的找出，则充分利用题干“、分别是、边上的高”中的垂直关系找到角相等的关系，再证明△CDA∽△CEB得到CD：CE=CA：CB从而运用比例的基本性质得到CD：CA=CE：CB.证明：∵在△ABC中，AD、BE分别是BC、AC边上的高∴∠ADC=∠BEC=90°∵∠C是公共角，∴△CDA∽△CEB（两组角对应相等的两个三角形相似）∴CD：CE=CA：CB（相似三角形对应边成比例）∴CD：CA=CE：CB（比例的基本性质）∴△DCE∽△ACB．（两组对应边的比相等且相应的夹角相等的两个三角形相似）【点拨】本题考察了相似三角形的性质：相似三角形对应边成比例；相似三角形的判定定理：两组对应边的比相等且相应的夹角相等的两个三角形相似的综合运用，运用证明一个三角形相似得到的结论去证明另外一个三角形相似.【变式2】如图，在中，，，动点从点开始沿边运动，速度为；动点从点开始沿边运动，速度为；如果、两动点同时运动，那么何时与相似？ 【答案】经过2秒或0.8秒时，与相似．【分析】观察图形可得，与已经有公共角，根据题意需要考虑的两条边对应成比例，此时会出现两种情况，和，可设经过秒时与相似，用时间分别表示出相关线段的长度，代入比例式解答即可.解：设经过秒时，与相似，则，，，，当时，，即，解得；当时，，即，解得；即经过2秒或0.8秒时，与相似．【点拨】本题是结合了相似三角形的判定的动点问题，在运动过程中寻找符合要求的节点，转化为判定三角形的相似是解答关键.类型三、非平行A字型（母子型）3．已知，如图，△ABC中，AB＝4，BC＝8，D为BC边上一点，BD＝2．求证：△ABD∽△CBA．   【分析】由AB＝4，BC＝8，BD＝2可知，再由∠ABD＝∠CBA可得△ABD∽△CBA；证明：∵AB＝4，BC＝8，BD＝2，∴，又∵∠ABD＝∠CBA，∴△ABD∽△CBA．【点拨】本题考查相似三角形的判定，熟练掌握相似三角形的判定方法是解决本题的关键．举一反三【变式1】如图，在△ABC中，点D是边AB上的一点，∠ADC=∠ACB，AD=2，BD=6．(1)  求证：△ACD∽△ABC；   (2) 求边AC的长．     【答案】(1) 证明见分析 (2)  4【分析】（1）直接利用相似三角形的判定即可得证；（2）先根据线段和差可得，再根据相似三角形的性质即可得．（1）证明：在和中，，．（2）解：，，由（1）已证：，，即，解得或（不符题意，舍去），经检验，是所列分式方程的解，则边的长为4．【点拨】本题考查了相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解题关键．【变式2】（1）如图1，在△ABC中，D为AB上一点，∠BCD=∠A，求证：BC=BD•AB（2）如图2，在△ABC中，AB=AC，∠BAC=36°，CD平分∠ACB，若BC=1，求AB的长．  【答案】（1）见分析；（2）【分析】（1）证明△BDC∽△BCA，由相似的性质可以得出．则可以得出结论．（2）证明△ABC∽△CBD，可得，设BD=x，则AB=x+1，得出，解出方程即可得到答案．解：（1）∵∠BCD＝∠A，∠B＝∠B∴△BDC∽△BCA∴∴（2）∵AB＝AC，∠BAC=36°∴∠B＝∠ACB＝72°∵CD平分∠ACB∴∠ACD＝∠BCD＝36°＝∠A∴∠BDC＝72°＝∠ACB∵∠B＝∠B∴△ABC∽△CBD∴∵∠BDC＝∠B＝72°∴BC=CD=1∵∠ACD＝∠A＝36°∴AD=BC=CD=1设BD=x，则AB=x+1∴即解得：（负值舍去）∴∴【点拨】本题考查了相似三角形的判定和性质，证明三角形是相似三角形是解决问题的关键．