初中北师大版第一章 特殊平行四边形2 矩形的性质与判定课堂教学ppt课件

这是一份初中北师大版第一章 特殊平行四边形2 矩形的性质与判定课堂教学ppt课件，共15页。PPT课件主要包含了学习目标，情境导入，探索交流，例题解析，∴ACBD，练习巩固等内容，欢迎下载使用。
1.掌握矩形的性质及判定方法2.会运用矩形的性质及判定方法进行计算和证明（重点）3.矩形的性质和判定方法与其他有关知识的综合运用（难点）
有三个角是直角的四边形是矩形.
有一个角是直角的平行四边形.
对角线相等的平行四边形是矩形.
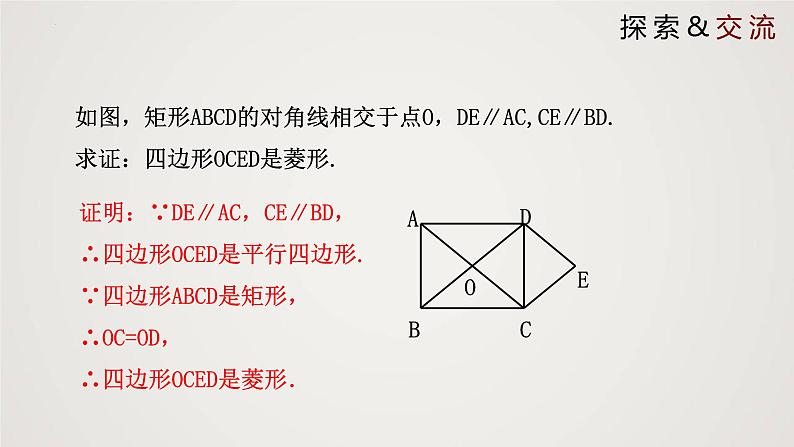
如图，矩形ABCD的对角线相交于点O，DE∥AC,CE∥BD.求证：四边形OCED是菱形.
证明：∵DE∥AC，CE∥BD，∴四边形OCED是平行四边形.∵四边形ABCD是矩形，∴OC=OD，∴四边形OCED是菱形．
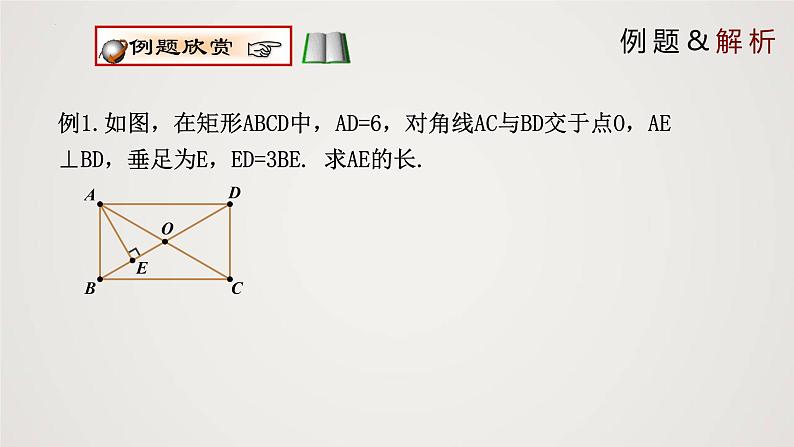
例1.如图，在矩形ABCD中，AD=6，对角线AC与BD交于点O，AE ⊥BD，垂足为E，ED=3BE. 求AE的长.
解∵ 四边形 ABCD 是矩形，∴∠BAD = 90°（矩形的四个都是直角），AC = BD（矩形的对角线相等）AO = CO = AC，BO=DO = BD（矩形的对角线互相平分）.∴AO = BO = DO = BD.∵ED = 3BE，∴BE = OE，又∵AE⊥BD，∴AB = AO. ∴AB = AO = BO，即 △ABO是等边三角形. ∴∠ABO = 60°.∴∠ADB = 90°-∠ABO = 90°- 60°= 30°.∴AE = AD = ×6 = 3.
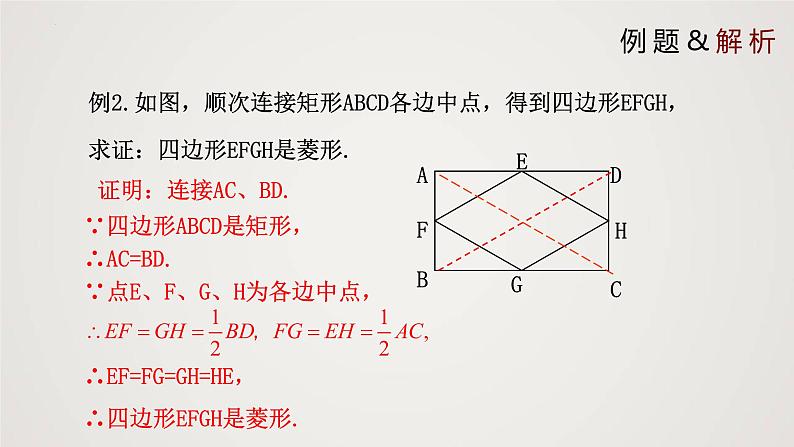
证明：连接AC、BD.
∵四边形ABCD是矩形，
∵点E、F、G、H为各边中点，
∴EF=FG=GH=HE，
∴四边形EFGH是菱形.
例2.如图，顺次连接矩形ABCD各边中点，得到四边形EFGH，求证：四边形EFGH是菱形.
例3.已知：如图，在△ABC中，AB=AC，AD是△ABC的一条角平分线，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E．（1）求证：四边形ADCE为矩形；（2）连接DE，交AC于点F，请判断四边形ABDE的形状，并证明；（3）线段DF与AB有怎样的关系？请直接写出你的结论.
（1）求证：四边形ADCE为矩形；
（1）证明：∵在△ABC中，AB=AC，AD是BC边的中线，∴AD⊥BC，∠BAD=∠CAD，∴∠ADC=90°，∵AN为△ABC的外角∠CAM的平分线，∴∠MAN=∠CAN，∴∠DAE=90°，∵CE⊥AN，∴∠AEC=90°，∴四边形ADCE为矩形；
解：四边形ABDE是平行四边形，理由如下：由（1）知，四边形ADCE为矩形，则AE=CD，AC=DE．又∵AB=AC，BD=CD，∴AB=DE，AE=BD，∴四边形ABDE是平行四边形；
（2）连接DE，交AC于点F，请判断四边形ABDE的形状，并证明；
解：DF∥AB，DF= AB．理由如下：∵四边形ADCE为矩形，∴AF=CF，∵BD=CD，∴DF是△ABC的中位线，∴DF∥AB，DF= AB
（3）线段DF与AB有怎样的关系？请直接写出你的结论.
1.如图，四边形ABCD和四边形AEFC是两个矩形，点B在EF边上，若矩形ABCD和矩形AEFC的面积分别是S1，S2，则S1，S2的大小关系是(　 　)A．S1>S2　　　　　　　B．S1＝S2C．S1