专题11.3 与三角形有关的角-（ 学案讲义） 八年级数学上册基础知识专项讲练-（人教版）

这是一份专题11.3 与三角形有关的角-（ 学案讲义） 八年级数学上册基础知识专项讲练-（人教版），共8页。
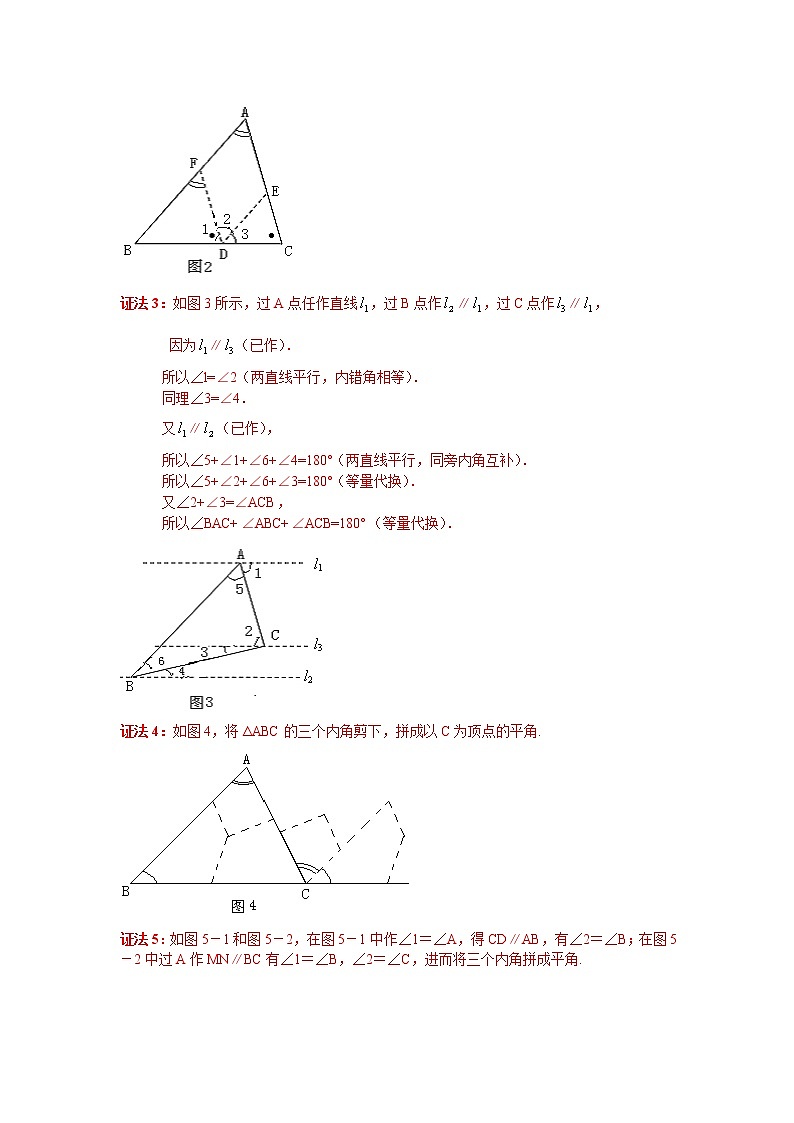
专题11.3  与三角形有关的角（知识讲解） 【学习目标】1．理解三角形内角和定理的证明方法；2．掌握三角形内角和定理及三角形的外角性质；3．能够运用三角形内角和定理及三角形的外角性质进行相关的计算，证明问题.【要点梳理】要点一、三角形的内角1. 三角形内角和定理：三角形的内角和为180°．要点诠释：应用三角形内角和定理可以解决以下三类问题：①在三角形中已知任意两个角的度数可以求出第三个角的度数；②已知三角形三个内角的关系，可以求出其内角的度数；③求一个三角形中各角之间的关系．2. 直角三角形：如果一个三角形是直角三角形，那么这个三角形有两个角互余.反过来，有两个角互余的三角形是直角三角形.要点诠释：如果直角三角形中有一个锐角为45°，那么这个直角三角形的另一个锐角也是45°，且此直角三角形是等腰直角三角形.要点二、三角形的外角1．定义：三角形的一边与另一边的延长线组成的角叫做三角形的外角．如图，∠ACD是△ABC的一个外角.要点诠释：(1)外角的特征：①顶点在三角形的一个顶点上； ②一条边是三角形的一边；③另一条边是三角形某条边的延长线． （2）三角形每个顶点处有两个外角，它们是对顶角．所以三角形共有六个外角，通常每个顶点处取一个外角，因此，我们常说三角形有三个外角．2．性质：（1）三角形的一个外角等于与它不相邻的两个内角的和． （2）三角形的一个外角大于任意一个与它不相邻的内角．要点诠释：三角形内角和定理和三角形外角的性质是求角度及与角有关的推理论证明经常使用的理论依据．另外，在证角的不等关系时也常想到外角的性质．3.三角形的外角和：   三角形的外角和等于360°.要点诠释：因为三角形的每个外角与它相邻的内角是邻补角，由三角形的内角和是180°，可推出三角形的三个外角和是360°．【典型例题】类型一、三角形的内角和 1．证明：三角形的内角和为180°.【答案与解析】解：已知：如图，已知△ABC，求证：∠A+∠B+∠C＝180°.     证法1：如图1所示，延长BC到E，作CD∥AB．因为AB∥CD（已作），所以∠1=∠A（两直线平行，内错角相等），∠B=∠2（两直线平行，同位角相等）．    又∠ACB+∠1+∠2=180°（平角定义），    所以∠ACB+∠A+∠B=180°（等量代换）．证法2：如图2所示，在BC边上任取一点D，作DE∥AB，交AC于E，DF∥AC，交AB于点F．因为DF∥AC（已作），所以∠1=∠C（两直线平行，同位角相等），∠2=∠DEC（两直线平行，内错角相等）．因为DE∥AB（已作）．所以∠3=∠B，∠DEC=∠A（两直线平行，同位角相等）．所以∠A=∠2（等量代换）．又∠1+∠2+∠3=180°（平角定义），所以∠A+∠B+∠C=180°（等量代换）．证法3：如图3所示，过A点任作直线，过B点作∥，过C点作∥，       因为∥（已作）．      所以∠l=∠2（两直线平行，内错角相等）．      同理∠3=∠4．又∥（已作），所以∠5+∠1+∠6+∠4=180°（两直线平行，同旁内角互补）．      所以∠5+∠2+∠6+∠3=180°（等量代换）．      又∠2+∠3=∠ACB，      所以∠BAC+∠ABC+∠ACB=180°（等量代换）．证法4：如图4，将ΔABC的三个内角剪下，拼成以C为顶点的平角.证法5：如图5－1和图5－2，在图5－1中作∠1＝∠A，得CD∥AB，有∠2＝∠B；在图5－2中过A作MN∥BC有∠1＝∠B，∠2＝∠C，进而将三个内角拼成平角.【总结升华】三角形内角和定理的证明方法有很多种，无论哪种证明方法，都是应用的平行线的性质.2.在△ABC中，已知∠A+∠B＝80°，∠C＝2∠B，试求∠A，∠B和∠C的度数．【思路点拨】题中给出两个条件：∠A+∠B＝80°，∠C＝2∠B，再根据三角形的内角和等于180°，即∠A+∠B+∠C＝180°就可以求出∠A，∠B和∠C的度数．【答案与解析】解：由∠A+∠B＝80°及∠A+∠B+∠C＝180°，    知∠C＝100°．    又∵  ∠C＝2∠B，    ∴  ∠B＝50°．    ∴  ∠A＝80°-∠B＝80°-50°＝30°．【总结升华】解答本题的关键是利用隐含条件∠A+∠B+∠C＝180°．本题可以设∠B＝x，则∠A＝80°-x，∠C＝2x建立方程求解．举一反三：【变式】  如图，在△ABC中，∠A=50°，E是△ABC内一点，∠BEC=150°，∠ABE的平分线与∠ACE的平分线相交于点D，则∠BDC的度数为多少？【答案】100°.解：∵△ABC中∠A=50°，∴∠ABC+∠ACB=180°﹣50°=130°，∵△BCE中∠E=150°，∴∠EBC+∠ECB=180°﹣150°=30°，∴∠ABE+∠ACE=130°﹣30°=100°，∵∠ABE的平分线与∠ACE的平分线相交于点D，∴∠DBE+∠DCE=（∠ABE+∠ACE）=×100°=50°，∴∠DBE+∠DCE=（∠DBE+∠DCE）+（∠EBC+∠ECB）=50°+30°=80°，∴∠BDC=180°﹣80°=100°．类型二、三角形的外角 3.（1）如图，AB和CD交于点O，求证：∠A＋∠C＝∠B＋∠D ．（2）如图，求证：∠D=∠A＋∠B +∠C．【答案与解析】解：（1）如图，在△AOC中，∠COB是一个外角，由外角的性质可得：∠COB＝∠A＋∠C，同理，在△BOD中，∠COB＝∠B＋∠D，所以∠A＋∠C＝∠B＋∠D．（2）如图，延长线段BD交线段于点E,在△ABE中，∠BEC＝∠A＋∠B  ①；在△DCE中，∠BDC＝∠BEC＋∠C  ②，将①代入②得，∠BDC＝∠A＋∠B＋∠C，即得证．【总结升华】重要结论：（1）“8”字形图：∠A＋∠C＝∠B＋∠D；（2）“燕尾形图”：∠D=∠A＋∠B +∠C．举一反三：【变式1】 如图，AB∥CD，AD和BC相交于点O，∠A＝40°，∠AOB＝75°，则∠C等于（　　）.     A、40°     B、65°           C、75°  D、115°【答案】B.【变式2】如图，在△ABC中，∠A＝70°，BO，CO分别平分∠ABC和∠ACB，则∠BOC的度数为       .【答案】125°.类型三、三角形的内角外角综合4. 已知如图∠xOy=90°，BE是∠ABy的平分线，BE的反向延长线与∠OAB的平分线相交于点C，当点A，B分别在射线Ox，Oy上移动时，试问∠ACB的大小是否发生变化？如果保持不变，请说明理由；如果随点A，B的移动而变化，请求出变化范围．【思路点拨】根据角平分线的定义、三角形的内角和、外角性质求解．【答案与解析】解：∠C的大小保持不变．理由：∵∠ABY=90°+∠OAB，AC平分∠OAB，BE平分∠ABY，∴∠ABE=∠ABY=（90°+∠OAB）=45°+∠OAB，即∠ABE=45°+∠CAB，又∵∠ABE=∠C+∠CAB，∴∠C=45°，故∠ACB的大小不发生变化，且始终保持45°．【总结升华】本题考查的是三角形内角与外角的关系，掌握“三角形的内角和是180°”是解决问题的关键．举一反三：【变式】如图所示，已知△ABC中，P为内角平分线AD、BE、CF的交点，过点P作PG⊥BC于G，试说明∠BPD与∠CPG的大小关系并说明理由．【答案】 解：∠BPD＝∠CPG．理由如下：    ∵  AD、BE、CF分别是∠BAC、∠ABC、∠ACB的角平分线，    ∴  ∠1＝∠ABC，∠2＝∠BAC，∠3＝∠ACB．    ∴  ∠1+∠2+∠3＝(∠ABC+∠BAC+∠ACB)＝90°．又∵  ∠4＝∠1+∠2，∴  ∠4+∠3＝90°．又∵  PG⊥BC，∴  ∠3+∠5＝90°．    ∴ ∠4＝∠5，即∠BPD＝∠CPG．