








数学八年级下册4.5 一次函数的应用精品ppt课件
展开第4章 一次函数
4.5 一次函数的应用
第2课时 建立一次函数模型解决实际问题
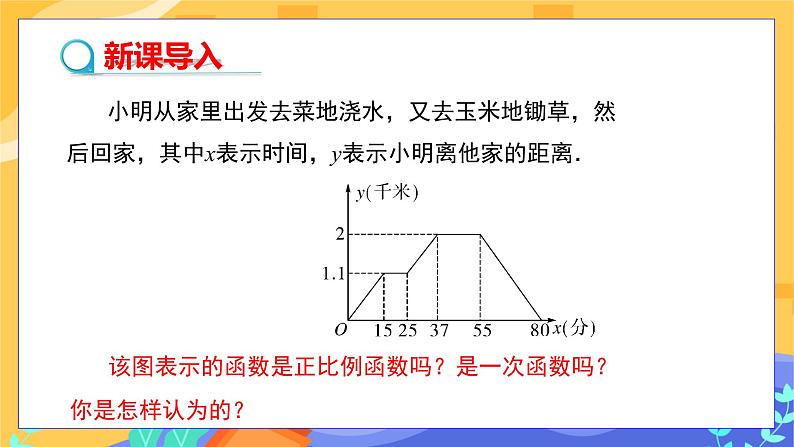
教学目标 1.能结合对函数关系的分析,对变量的变化情况进行初步讨论. 2.会用一次函数知识解决问题,进而体会函数模型思想. 教学重难点 重点:建立一次函数模型解决实际问题. 难点:建立一次函数模型解决实际问题. 教学过程 探究新知 问题:国际奥林匹克运动会早期,男子撑杆跳高的纪录近似值如下表所示:
观察这个表中第二行的数据,可以为奥运会的撑杆跳高纪录与时间的关系建立函数模型吗? 问题:能把这个问题描述为函数问题吗? 师生活动:学生独立建立函数模型,把实际问题转化为函数问题,并进行相互交流,教师引导学生解决函数问题. 学生:分析第二行的数据,每一届比上一届的纪录提高了0.2 m,可以试着建立一次函数的模型. 确定函数模型后,学生先设函数解析式,再利用待定系数法进行求解. 用t表示从1900年起增加的年份,则在奥运会早期,男子撑杆跳高的纪录y(m)与t的函数关系式可以设为 y=kt+b. 由于t=0(即1900年)时,撑杆跳高的纪录为3.33 m,t=4(即1904年)时,纪录为3.53m,因此
解得b=3.3,k=0.05. 于是y=0.05t+3.33. ① 教师:选取其中的两组数据得到的解析式一定准确吗?需要验证吗? 学生:需要代入第三组数据进行验证. 当t=8时, y = 3.73,这说明1908年的撑杆跳高纪录也符合公式①. 结论:公式①就是奥运会早期男子撑杆跳高纪录y与时间t之间的函数关系式. 思考:能够利用上面得出的公式①预测1912年奥运会的男子撑杆跳高纪录吗?(这就是已知自变量求函数值) 解答:y=0.05×12+3.33=3.93. 实际上,1912 年奥运会男子撑杆跳高纪录约为3.93 m. 这表明用所建立的函数模型,在已知数据邻近做预测,结果与实际情况比较吻合. 思考:能够利用公式①预测20世纪80年代,譬如1988年奥运会男子撑杆跳高纪录吗? 解答:y=0.05×88+3.33=7.73. 1988年奥运会的男子撑杆跳高纪录是5.90 m, 远低于7.73 m. 这表明用所建立的函数模型远离已知数据做预测是不可靠的. 归纳总结: 通过上面的学习,我们知道建立两个变量之间的函数模型,可以通过下列几个步骤完成: (1)找出因变量和自变量; (2)通过对应值发现对应关系,抽象函数表达式; (3)验证并化简函数表达式,得到问题的规律; (4)应用这个函数模型解决问题. 新知应用 例 请每位同学伸出一只手掌,把大拇指与小拇指尽量张开,两指间的距离称为指距. 已知指距与身高具有如下关系:
(1) 求身高y与指距x之间的函数表达式; (2) 当李华的指距为22 cm时,你能预测他的身高吗? 分析:上表3组数据反映了身高y与指距x之间的对应关系, 观察这两个变量之间的变化规律,当指距增加1 cm时, 身高就增加9 cm,可以尝试建立一次函数模型. 解:(1)设身高y与指距x之间的函数表达式为y=kx+b. 将x=19, y=151与x=20,y=160代入上式,得
解得k=9, b=-20. 于是y=9x-20. ① 将x=21,y = 169代入①式也符合. 公式①就是身高y与指距x之间的函数表达式. (2)当x=22时, y=9×22-20=178. 因此,李华的身高大约是178 cm. 课堂小结 在本节课中,我们经历了怎样的过程?有怎样的收获? 建立一次函数模型的步骤: (1)找出因变量和自变量; (2)通过对应值发现对应关系,抽象函数表达式; (3)验证并化简函数表达式,得到问题的规律; (4)应用这个函数模型解决问题. 布置作业 教材第140页习题4.5第3,4题. 板书设计 4.5 一次函数的应用 第2课时 建立一次函数模型解决实际问题 |
初中数学第4章 一次函数4.5 一次函数的应用一等奖课件ppt: 这是一份初中数学第4章 一次函数4.5 一次函数的应用一等奖课件ppt,文件包含第2课时建立一次函数模型解决预测类型的实际问题课件pptx、第1课时利用一次函数解决实际问题课件pptx、第3课时一次函数与一次方程的联系课件pptx、45一次函数的应用练习pptx、第1课时利用一次函数解决实际问题教案doc、第2课时建立一次函数模型解决预测类型的实际问题教案doc、第3课时一次函数与一次方程的联系教案doc等7份课件配套教学资源,其中PPT共78页, 欢迎下载使用。
初中湘教版4.5 一次函数的应用获奖ppt课件: 这是一份初中湘教版4.5 一次函数的应用获奖ppt课件,文件包含第2课时建立一次函数模型解决预测类型的实际问题课件pptx、第1课时利用一次函数解决实际问题课件pptx、第3课时一次函数与一次方程的联系课件pptx、45一次函数的应用练习pptx、第1课时利用一次函数解决实际问题教案doc、第2课时建立一次函数模型解决预测类型的实际问题教案doc、第3课时一次函数与一次方程的联系教案doc等7份课件配套教学资源,其中PPT共78页, 欢迎下载使用。
初中数学湘教版八年级下册4.5 一次函数的应用一等奖ppt课件: 这是一份初中数学湘教版八年级下册4.5 一次函数的应用一等奖ppt课件,文件包含教学课件八下·湘教·45一次函数的应用第3课时一次函数与一次方程的关系pptx、45一次函数的应用第3课时教案docx、45一次函数的应用第3课时同步练习docx等3份课件配套教学资源,其中PPT共23页, 欢迎下载使用。













