中考数学一轮复习专题讲义——相似三角形与圆

这是一份中考数学一轮复习专题讲义——相似三角形与圆，文件包含第7讲-几何变换之旋转一docx、第8讲-几何变换之旋转二docx、第10讲-圆综合docx、第9讲-圆的切线docx、第4讲-二次函数中的特殊角问题docx、第2讲-特殊四边形存在性问题docx、第1讲-特殊三角形存在性问题docx、第13讲-二次函数综合一-参考答案docx、第1讲-特殊三角形存在性问题参考答案doc、第9讲-圆的切线参考答案doc、第3讲-二次函数中的线段与面积问题docx、第4讲-二次函数中的特殊角问题参考答案doc、第7讲-几何变换之旋转一参考答案doc、第12讲-动点与函数图像问题docx、第11讲-动态中的面积与图形存在性问题参考答案doc、第6讲-几何变换之对称参考答案doc、第6讲-几何变换之对称docx、第5讲-相似三角形存在性问题参考答案doc、第5讲-相似三角形存在性问题docx、第3讲-二次函数中的线段与面积问题参考答案doc、第10讲-圆综合参考答案doc、第2讲-特殊四边形存在性问题参考答案doc、第12讲-动点与函数图像问题参考答案doc、第8讲-几何变换之旋转二参考答案doc、第11讲-动态中的面积与图形存在性问题docx、第14讲-二次函数综合二-参考答案docx、第13讲-二次函数综合一docx、第14讲-二次函数综合二docx等28份试卷配套教学资源，其中试卷共225页， 欢迎下载使用。
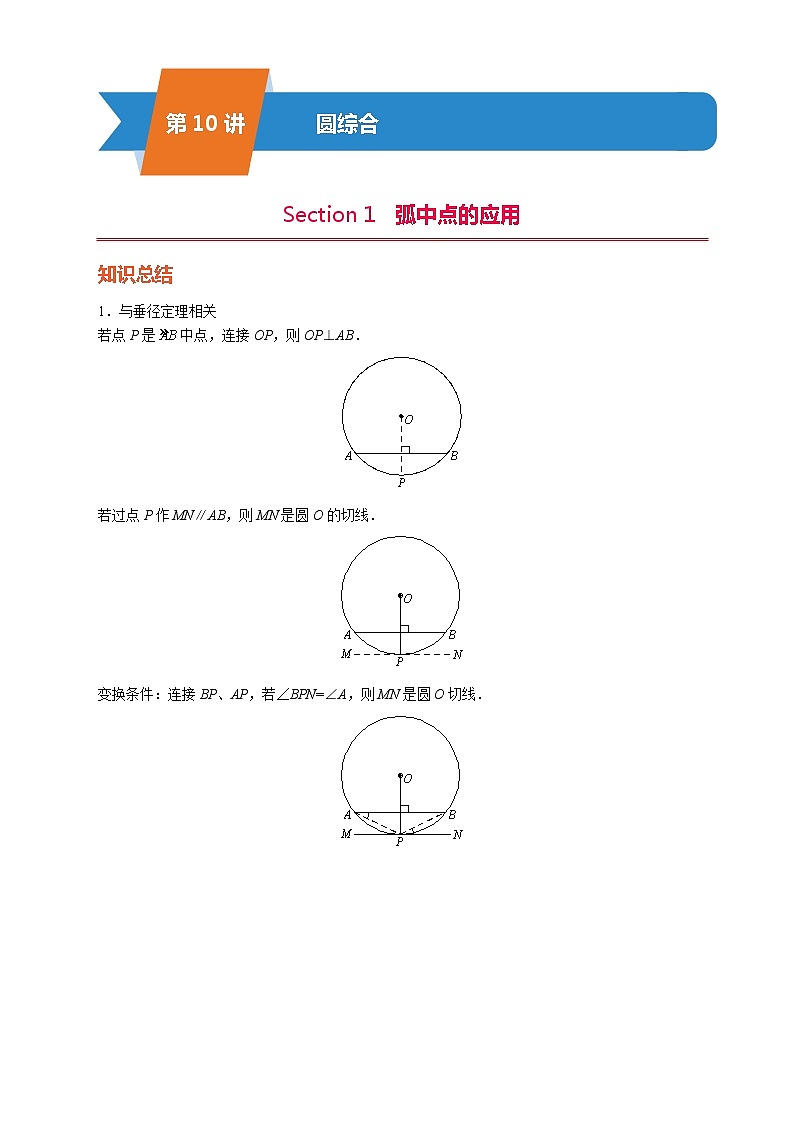
知识总结
切线的性质：垂直于过切点的半径．（连半径，得垂直）
切线的判定：
（1）定义法：和圆只有一个交点的直线是圆的切线；
（2）距离法：到圆心距离等于半径的直线是圆的切线；
证明d=r即可，常用于已知数据的计算，比如动圆相切问题．
（3）判定定理：经过半径外端且垂直于这条半径的直线是圆的切线．
换个说法：，多用于几何证明．
多数情况为有交点，重点考虑如何证垂直：①证明和已知垂线平行；②证明夹角为直角．
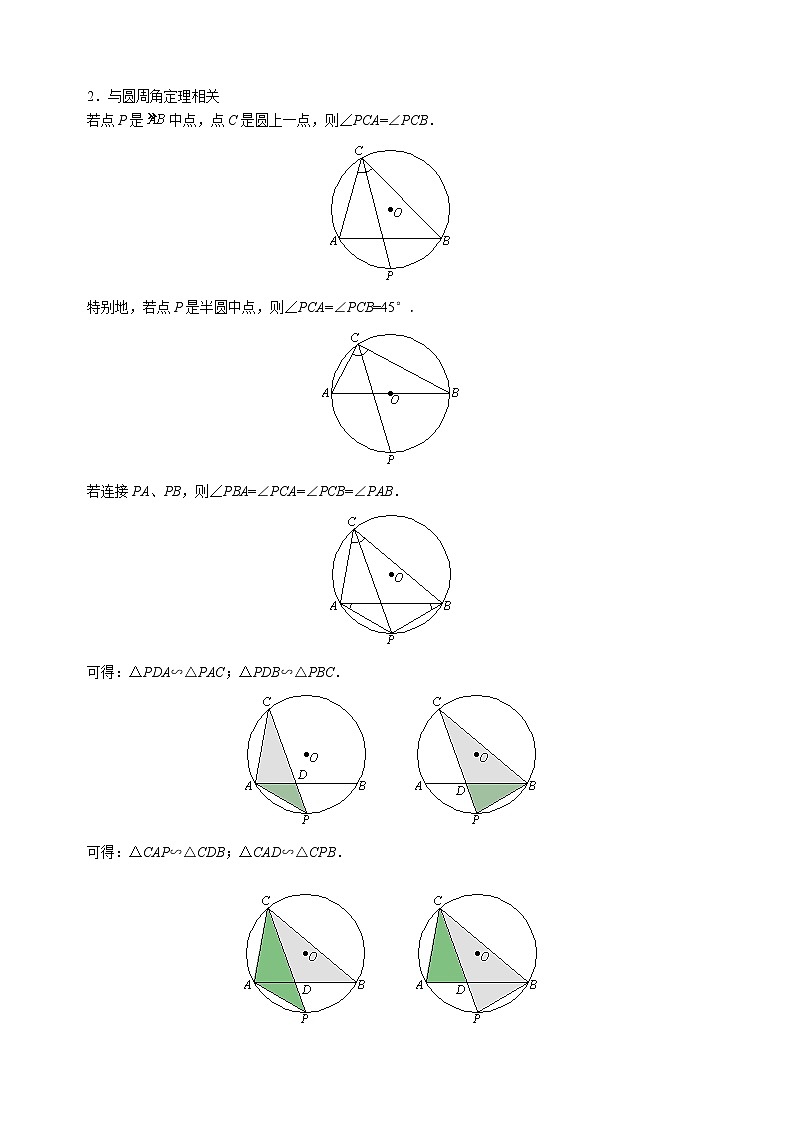
常见相切图
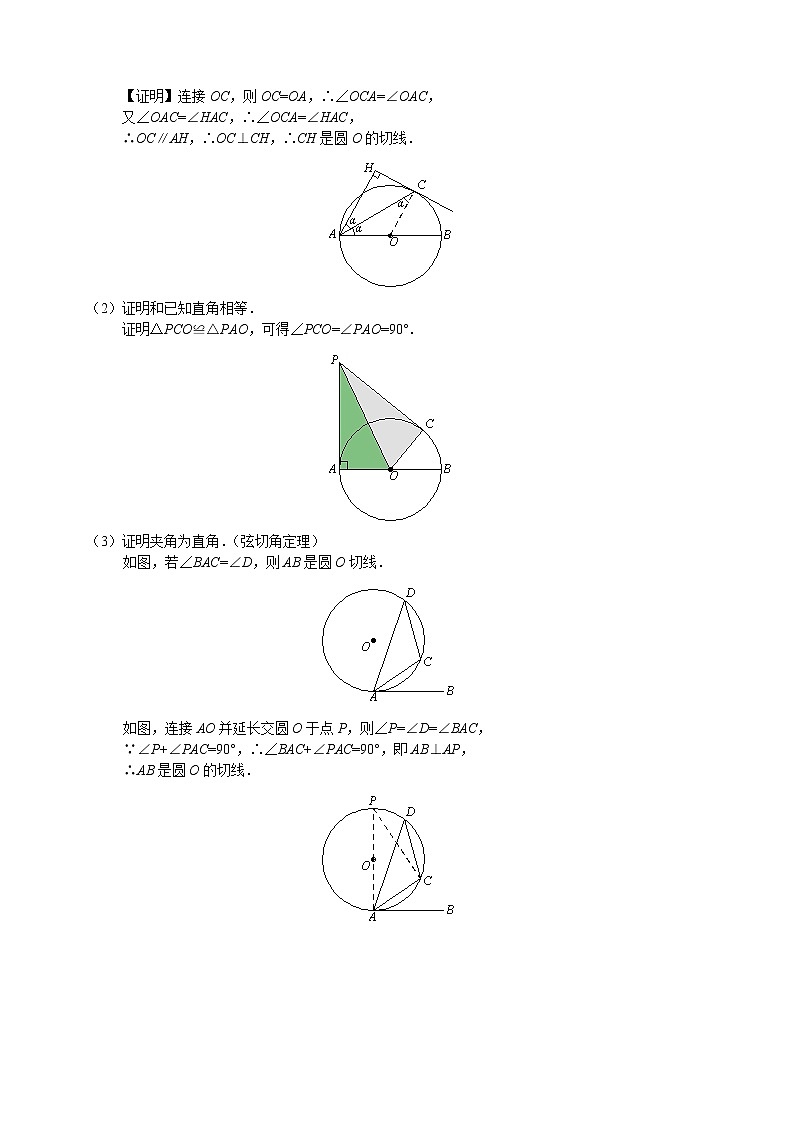
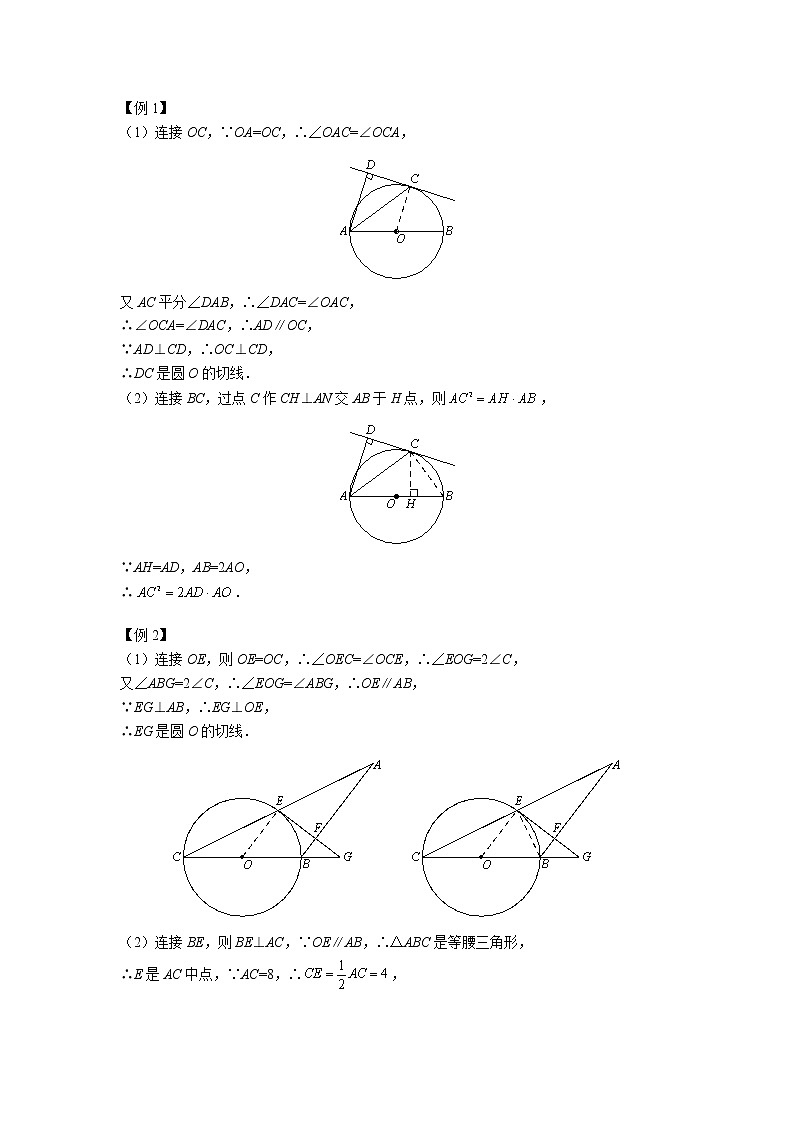
（1）角分+等腰得平行：点C在以AB为直径的圆O上，AH⊥CH，且AC平分∠HAB．
【证明】连接OC，则OC=OA，∴∠OCA=∠OAC，
又∠OAC=∠HAC，∴∠OCA=∠HAC，
∴OC∥AH，∴OC⊥CH，∴CH是圆O的切线．
（2）证明和已知直角相等．
证明△PCO≌△PAO，可得∠PCO=∠PAO=90°．
（3）证明夹角为直角．（弦切角定理）
如图，若∠BAC=∠D，则AB是圆O切线．
如图，连接AO并延长交圆O于点P，则∠P=∠D=∠BAC，
∵∠P+∠PAC=90°，∴∠BAC+∠PAC=90°，即AB⊥AP，
∴AB是圆O的切线．
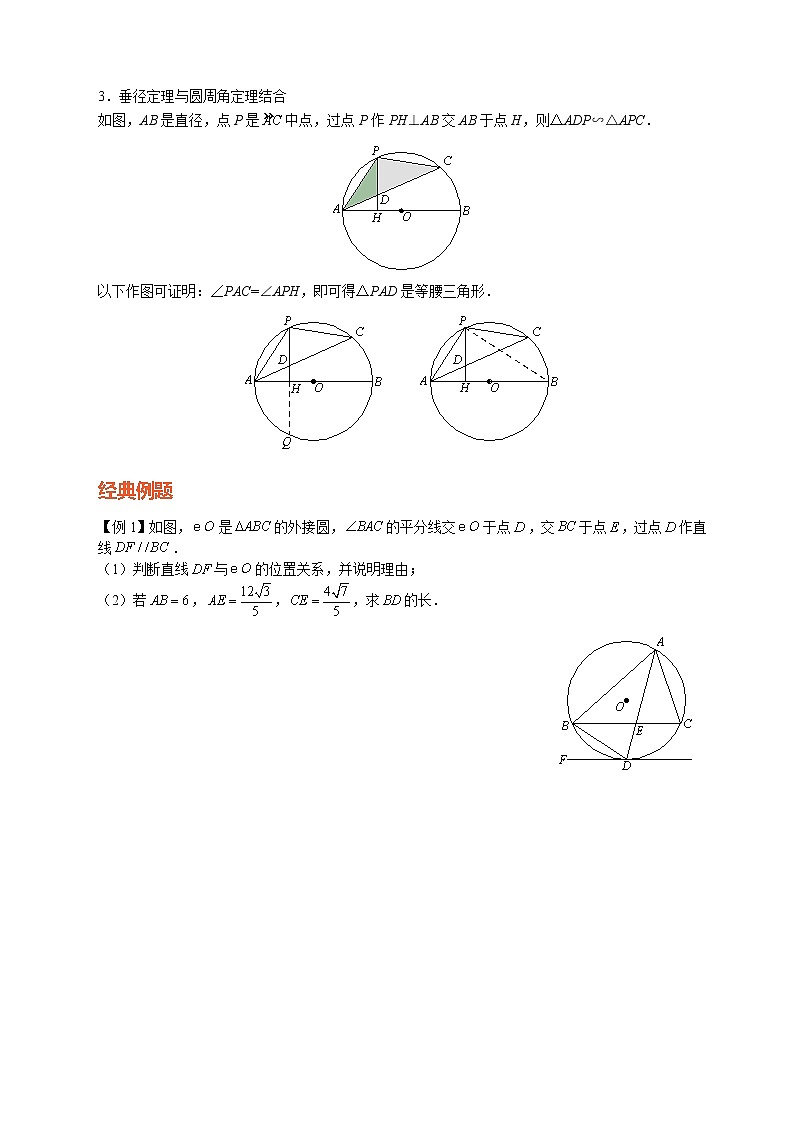
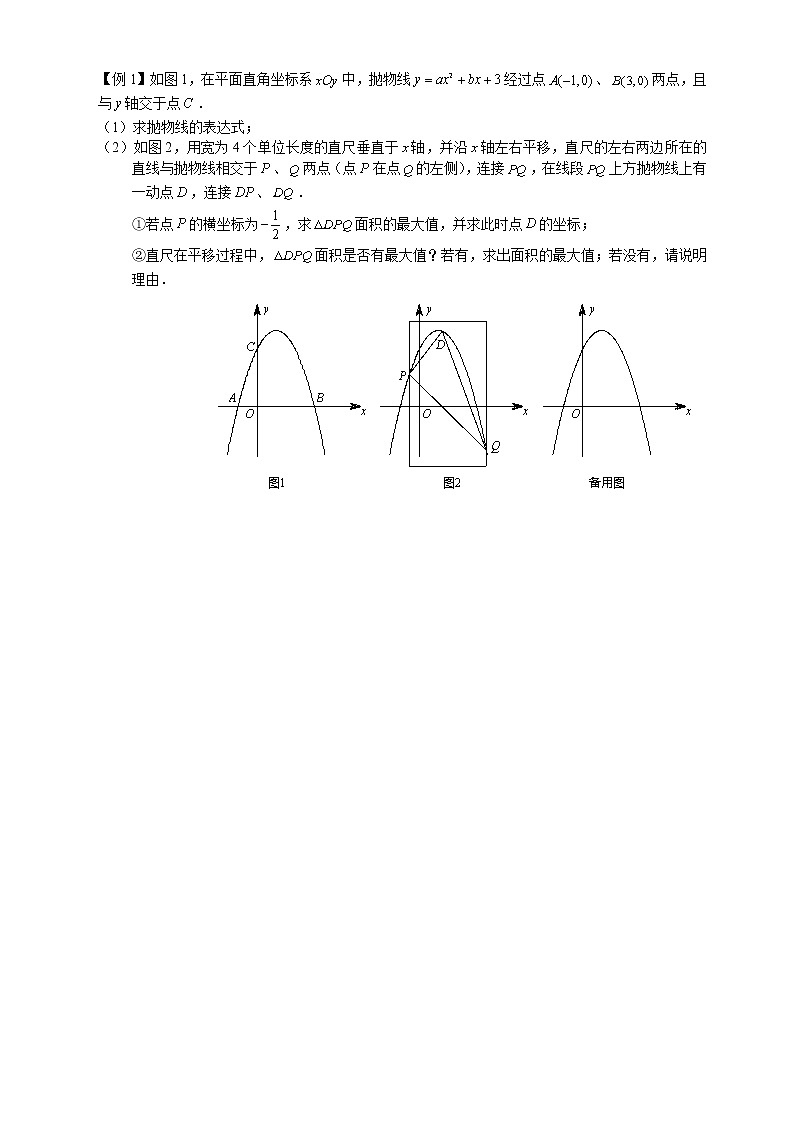
经典例题
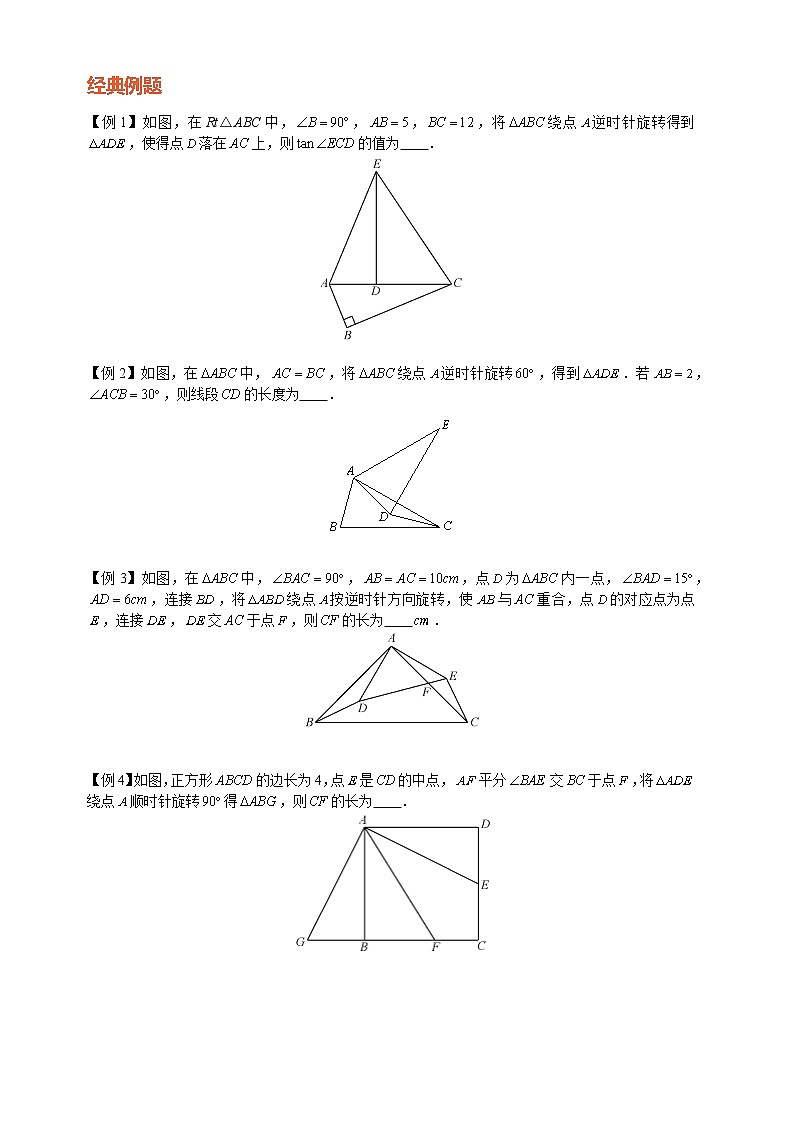
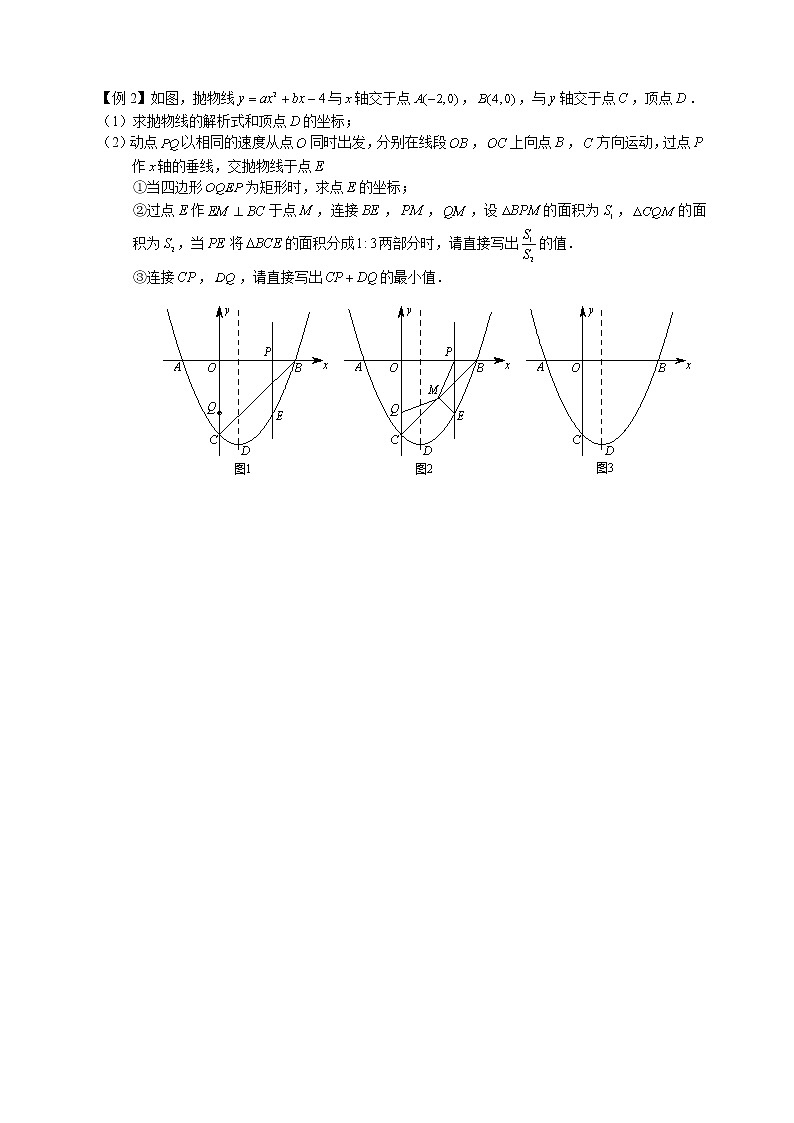
【例1】如图，为的直径，点在上，于点，且平分．
求证：（1）直线是的切线；
（2）．
【例2】如图， 在△ABC中， 以BC为直径的圆C交AC于点E，过点E作AB的垂线交AB于点F，交CB的延长线于点G，且∠ABG=2∠C．
（1） 求证： EG是圆O的切线；
（2） 若，AC=8，求圆O的半径 ．
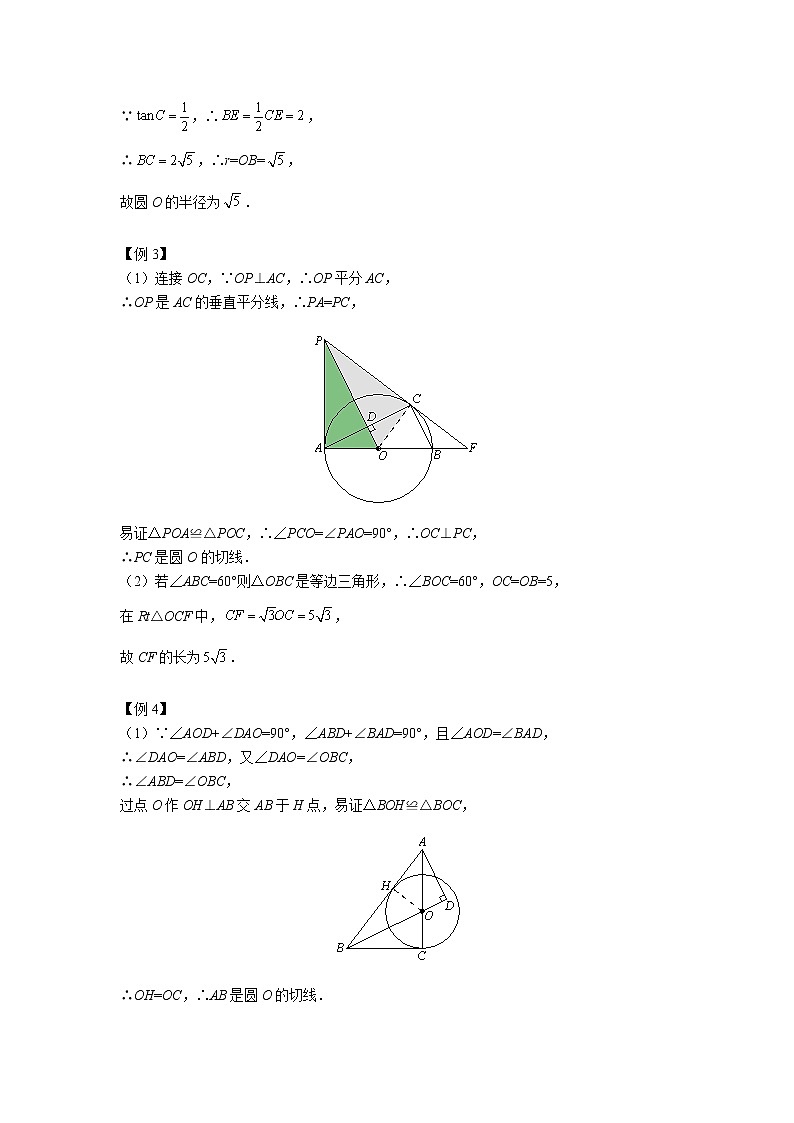
【例3】如图，、分别是的直径和弦，于点．过点作的切线与的延长线交于点，、的延长线交于点．
（1）求证：是的切线；
（2）若，，求线段的长．
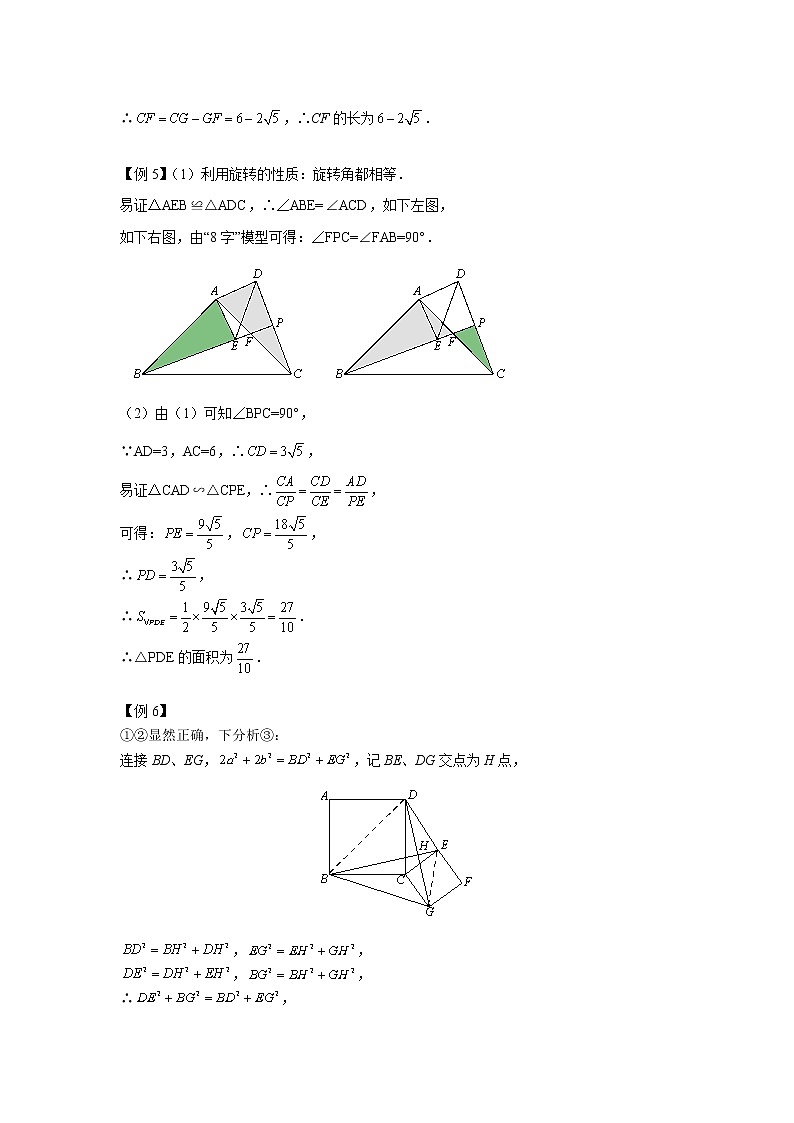
【例4】如图，在△ABC中，O为AC上一点，以点O为圆心，OC为半径做圆，与BC相切于点C，过点A作AD⊥BO交BO的延长线于点D，且∠AOD＝∠BAD．
（1）求证：AB为⊙O的切线；
（2）若BC＝6，tan∠ABC＝，求AD的长．
动圆相切问题
知识总结
类型一、动点为圆心：利用d=r计算．
【引例】如图，直线l的解析式为，点P坐标为，以点P为圆心，1为半径作圆，当点P以每秒2个单位的速度向右移动时，时间t为何值时圆P与直线l相切？
【分析】过点P作PH⊥直线l，垂足为H点，当PH=r=1时，即可得圆P与直线l相切．
当点P坐标为或时，PH=1，，，
综上所述，t的值为1或3．
经典例题
【例5】以坐标原点为圆心，作半径为2的圆，直线与相交，的取值范围是
A．B．C．D．
【例6】如图，Rt△ABC中，，，点在边上，，．点是线段上一动点，当半径为6的与的一边相切时，的长为 ．
【例7】如图，正方形的边长为8，是的中点，是边上的动点，连结，以点为圆心，长为半径作．当与正方形的边相切时，的长为 ．
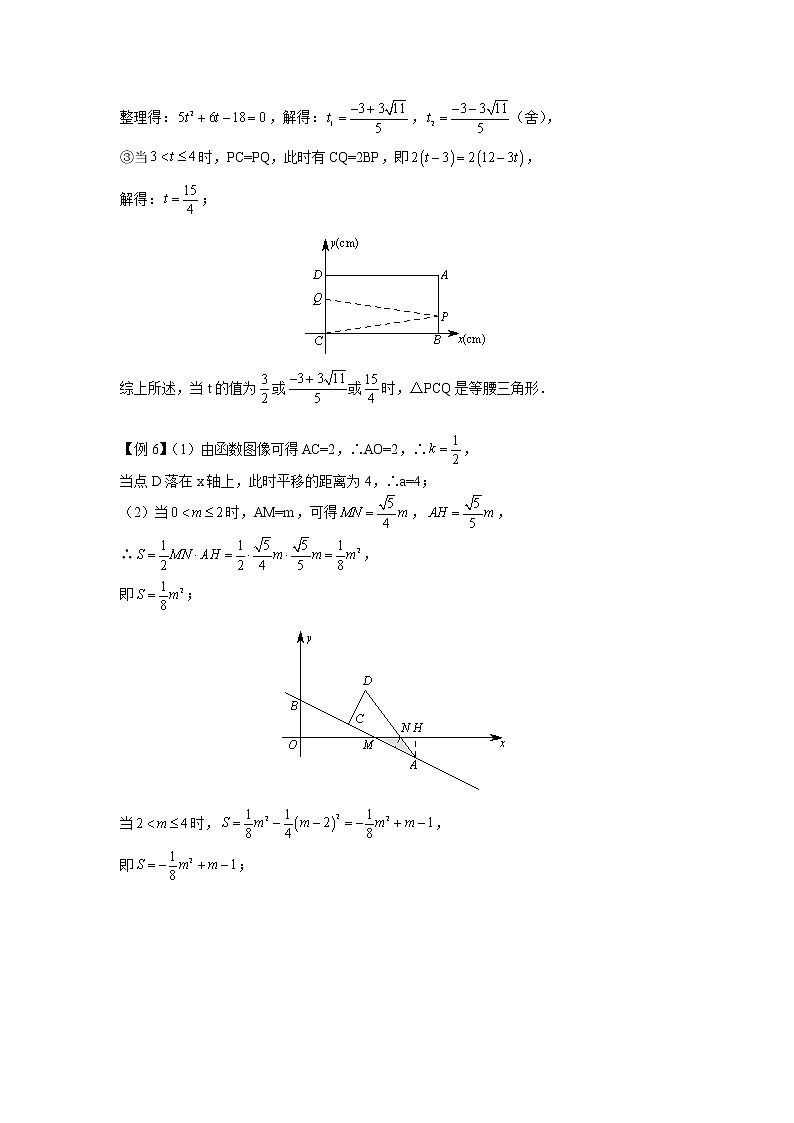
【例8】（2016·苏州）如图，在矩形ABCD中，AB=6cm，AD=8cm，点P从点B出发，沿对角线BD向点D匀速运动，速度为4cm/s，过点P作PQ⊥BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N落在射线PD上，点O从点D出发，沿DC向点C匀速运动，速度为3cm/s，以O为圆心，0.8cm为半径作圆O，点P与点O同时出发， 设它们的运动时间为t（单位：s）（）．
（1） 如图1，连接DQ平分∠BDC时，t的值为 ；
（2） 如图2，连接CM，若△CMQ是以CQ为底的等腰三角形，求t的值；
（3） 请你继续进行探究，并解答下列问题：
①证明：在运动过程中，点O始终在QM所在直线的左侧；
②如图3，在运动过程中，当QM与圆O相切时，求t的值；并判断此时PM与圆O是否也相切？说明理由 ．
类型二、动点为直径：由性质所得的垂直关系利用三角函数计算．
【引例】在矩形ABCD中，AB=4，BC=3，连接BD，点P从D点出发以每秒1个单位向点C运动，点Q从点B出发以每秒2个单位向点D运动，以PQ中点O为圆心，PQ为直径作圆，运动时间t为何值时，圆O与BD相切？
【分析】当PQ⊥BD时，圆O与BD相切，
由题意得：DP=t，DQ=5-2t，若PA⊥BD，即，
代入得：，解得：，
故当t的值为时，圆O与BD相切．
【例9】（2018·相城区一模）如图，在Rt△ABC中，，，，动点从点出发，在边上以每秒的速度向点匀速运动，同时动点也从点出发，沿以每秒的速度匀速运动，运动时间为秒，连接，以为直径作．
（1）当时，求的面积；
（2）设的面积为，求与的函数关系式；
（3）当点在上运动时，与Rt△ABC的一边相切，求的值．
类型三、交点个数的分析
圆与线段或图形交点个数问题，考虑交点个数变化的位置，当①圆与线段相切、②圆过线段端点时，交点个数会发生改变．
【引例】如图，在坐标系中，点A坐标为（1，0），点B坐标为（0，3），以点P（m，0）（m