甘肃省酒泉市2022-2023学年五年级下学期数学期末调研试卷AB卷（含解析）

这是一份甘肃省酒泉市2022-2023学年五年级下学期数学期末调研试卷AB卷（含解析），共39页。试卷主要包含了脱式计算，解方程或比例，图形计算，选择题，填空题，解答题等内容，欢迎下载使用。

甘肃省酒泉市2022-2023学年五年级下学期数学期末调研
试卷（A卷）
一、脱式计算
1．（2022·甘肃·白银区第四小学五年级期末）计算下面各题。
                          




二、解方程或比例
2．（2021·吉林·德惠市米沙子镇沃皮中心小学五年级期中）解方程。
3x＋x＝                                        x—＝             
（—）x＝                                   x÷（1—）＝






三、图形计算
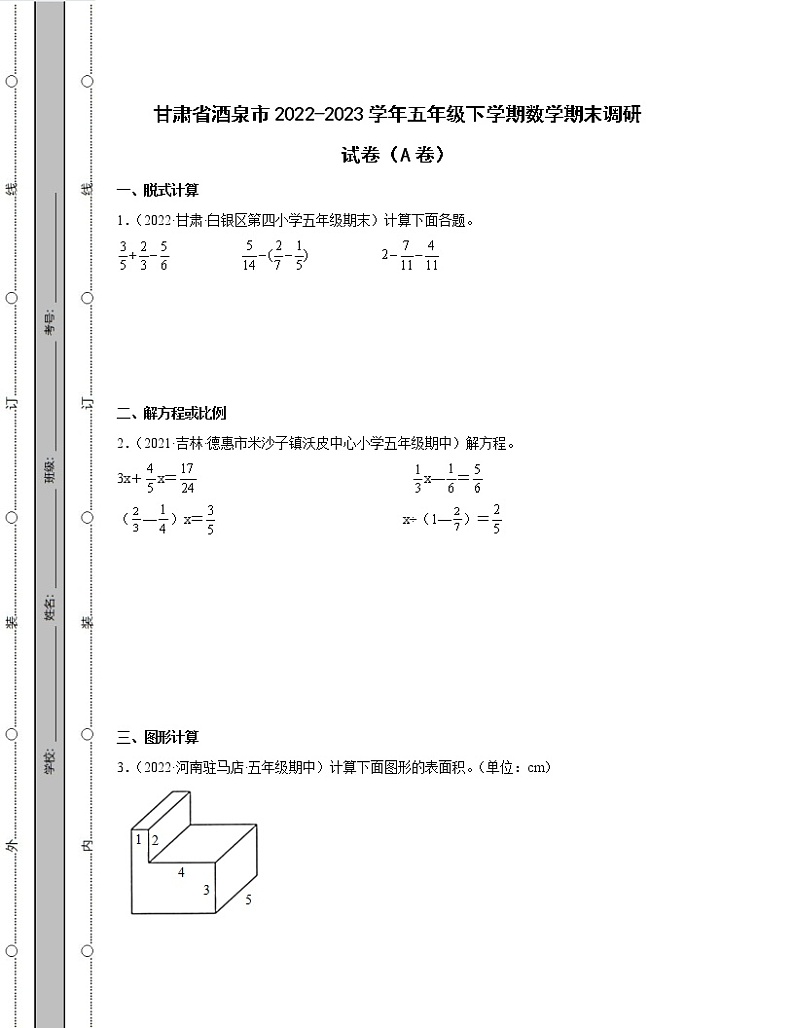
3．（2022·河南驻马店·五年级期中）计算下面图形的表面积。（单位：cm）





四、选择题
4．（2021·辽宁·五年级单元测试）一本书，第一天看了全书的，第二天又看了全书的。第二天比第一天少看了全书几分之几？正确的解答是（ ）
A． B． C． D．
5．（2022·湖南张家界·六年级期末）把两个棱长是10厘米的正方体拼成一个长方体后，表面积减少（       ）平方厘米。
A．100 B．200 C．80 D．300
6．（2021·江西萍乡·五年级期末）如果一个正方体的棱长扩大到原来的2倍，那么它的表面积就扩大到原来的（       ）倍。
A．2 B．4 C．6 D．8
7．（2021·辽宁·六年级期末）两个数的积在3和4之间的是（       ）。
A． B． C． D．
8．（2022·辽宁·五年级课时练习）棱长8cm的正方体与一个长方体的体积相等。已知长方体的高是16cm，那么它的底面积是（       ）cm2。
A．0.5 B．128 C．32 D．64
9．（·北京海淀·五年级期末）下面的问题中，不能用“”解决的是（       ）。
A．小妍做一个中国结需要米的红绳，24米红绳能做几个这样的中国结？
B．淘淘有24枚邮票，东东的邮票数是淘淘的。东东有多少枚邮票？
C．某小学举行诗词诵读大赛，有24名同学进入决赛，占初赛总人数的，共有多少名同学参加初奏？
D．王阿姨花24元买了千克樱桃，每千克樱桃多少钱？
10．（2020·四川乐山·六年级期末）广场为观测点，学校在北偏西30°的方向上，下图中正确的是（       ）。
A． B． C．
11．（2021·江苏·六年级单元测试）某大学今年参加“青年志愿者”的人数比去年多68人，今年的人数比去年的3倍少4人，今年有（       ）人参加。
A．36 B．104 C．108
五、填空题
12．（2021·河南许昌·五年级期末）在、、、这4个数中，( )最接近。
13．（2021·辽宁沈阳·五年级期末）（如图）将5个棱长是3分米的正方体靠墙角堆成一个立体图形，则露在外面的面的面积是( )平方分米。

14．（2021·山西运城·五年级期末）把3个棱长是的正方体木块拼成一个长方体，这个长方体的表面积是( )。
15．（2020·甘肃·玉门市教育局教育研究室五年级期末）18的等于36的( )；比2米少米是( )米；15分＝( )时；千克＝( )克。
16．（2022·广东惠州·五年级期中）一个正方体的棱长总和是24米，它的体积是( )立方米。
17．（2022·辽宁沈阳·六年级期末）一辆公交车出发时车上还有3个空座位，中途第一次停站时，车上有的乘客下车，又有12人上车，这时车上座位正好坐满。这辆公交车上一共有( )个座位。
18．（2021·辽宁·五年级单元测试）以电影院为观测点。

（1）学校在电影院的南偏( )( )°的方向上，距离电影院( )千米。
（2）儿童书店在电影院北偏( )( )°的方向上，距离电影院( )千米。
（3）超市在电影院北偏( )( )°的方向上，距离电影院( )千米。
19．（2020·广东湛江·五年级期末）某市农机一厂、二厂2019年工业产值增长情况统计图。

看图回答下列问题：
（1）一厂第二季度的产值是( )万元。
（2）农机二厂2019年平均每季度的产值是( )万元。
（3）( )厂第三季度增长幅度最大，增长了( )万元。
六、解答题
20．（2022·全国·五年级专题练习）甲乙两队合修一条公路，甲队修了全长的，乙队修了全长的，没修的占全部的几分之几？



21．（2020·北京·五年级期末）用木条做一个长方体框架，长为18cm，宽为12cm，高为10cm，至少需要多长的木条？




22．（2022·全国·五年级专题练习）一块长方形铁皮（如图），从四个角各切掉一个边长为3cm的正方形，然后做成盒子。这个盒子用了多少铁皮？它的容积有多少？




23．（2021·辽宁·六年级）一片地有50公顷，其中种水稻，水稻面积中的种糯稻。种糯稻多少公顷？




24．（2022·陕西西安·五年级期末）有一个棱长是5dm的正方体容器，里面水深3.5dm。这时往容器中放入一些小石块（浸没），水面离容器边沿还有0.8dm，这些石块的体积是多少？




25．（2021·北京·六年级专题练习）水果店购进40箱苹果，购进苹果的箱数是梨子箱数的。水果店购进了多少箱梨子？（用方程解）
26．（2021·黑龙江大兴安岭地·五年级期末）琪琪家到学校的路程是。琪琪从学校回家，每分走；妈妈从家出发骑车去学校接琪琪，每分行驶。两人同时出发，经过几分相遇？列方程解决问题。





27．（2021·黑龙江大兴安岭地·五年级期末）世界上现存的最大的鸟是鸵鸟，最高的陆生动物是长颈鹿。一只长颈鹿的身高是一只鸵鸟身高的1.8倍，长颈鹿比鸵鸟高。长颈鹿和鸵鸟的身高各是多少米？（列方程解决问题。）

答案：
1．；；1

【分析】
，根据分数加减法的计算法则，按照运算顺序，先计算加法，再计算减法。
，先计算括号里的减法，再计算括号外的减法；
，根据减法性质，原式化为：2－（＋），再进行计算。
【详解】

＝＋－
＝－
＝

＝－（－）
＝－
＝－
＝

＝2－（＋）
＝2－1
＝1
2．x＝；x＝3；
x＝；x＝

【分析】
先对方程的左边进行化简，再根据等式的性质，方程两边同时除以即可；
根据等式的性质，方程两边同时加上，再除以即可；
先对方程的左边进行化简，再根据等式的性质，方程两边同时除以即可；
先对方程的左边进行化简，再根据等式的性质，方程两边同时乘即可。
【详解】
3x＋x＝
解：x＝
x÷＝÷
x＝
x—＝
解：x—＋＝＋
x＝1
x÷＝1÷
x＝3
（—）x＝
解：x＝
x÷＝÷
x＝
x÷（1—）＝
解：x÷＝
x÷×＝×
x＝
3．134cm2

【分析】
认真观察此图形，可以将图形理解为上边一个小长方体，下边一个大长方体。把上边小长方体的上面下移到大长方体的上面，由此我们就可以分析出组合图形的表面积为一个长宽高分别为5cm、（4＋1）cm、3cm大长方体的表面积与一个长宽高分别为5cm、1cm、2cm的小长方体前后、左右四个面的面积之和。
【详解】
4＋1＝5（cm）
（5×5＋5×3＋5×3）×2＋5×2×2＋2×1×2
＝（25＋15＋15）×2＋10×2＋2×2
＝55×2＋20＋4
＝110＋20＋4
＝134（cm2）
4．A

【分析】
用第一天看的分率减去第二天看的分率，根据异分母分数减法的计算方法计算第二天比第一天少看的分率即可。
【详解】

故A

本题主要考查异分母分数减法的简单应用。
5．B

【分析】
表面积减少的部分是正方体的两个面，据此结合正方形的面积公式，列式计算即可。
【详解】
10×10×2＝200（平方厘米），所以把两个棱长是10厘米的正方体拼成一个长方体后，表面积减少200平方厘米。
故B

本题考查了正方体和长方体，两个正方体拼在一起后，表面积减少的部分恰好是正方体的两个面。
6．B

【分析】
正方体棱长扩大到原来的倍，表面积就扩大到原来的倍数，据此分析。
【详解】
2×2＝4
故B

关键是掌握正方体表面积公式，正方体表面积＝棱长×棱长×6。
7．A

【分析】
分数与分数相乘，分子与分子相乘作分子，分母与分母相乘作分母，能约分的先约分，计算出结果，再选择。
【详解】
A． ＝ ＝3 ，3＜3＜4；
B. ＝ ＝1， 1＜3；
C． ＝ ，＜3；
D． ＝ ＝4 ，4＞4
故选择：A

掌握分数与分数乘法的计算法则是解题关键。
8．C

【分析】
先计算出正方体的体积，根据“底面积＝体积÷高”即可解答。
【详解】
（8×8×8）÷16
＝512÷16
＝32（cm2）
故C

灵活运用长方体的体积公式是解答本题的关键。
9．B

【分析】
A．分数后面加单位表示具体的数，即根据总长度÷一个的长度＝总个数，由此即可分析。
B．通过题目可知淘淘是单位“1”，单位“1”已知用乘法，由此即可列式；
C．根据题目可知初赛总人数是单位“1”，单位“1”未知，用除法，由此即可列式；
D．根据公式：总钱数÷重量＝单价，由此列式即可。
【详解】
A．根据分析可知，总长度÷一个的长度＝总个数，即24÷；符合题意；
B．单位“1”已知用乘法，即24×；不符合题意；
C．根据公式对应量÷对应分率＝单位“1”，即24÷；符合题意；
D．根据分析可知，24÷，符合题意。
故B。

本题主要考查分数除法的列式，同时要注意，单位“1”已知用乘法，单位“1”未知用除法。
10．C

【分析】
根据“上北下南，左西右东”的方向确定北偏西的大致位置，再看角度是30°，即从正北向西偏的角度是30°，据此解答。
【详解】
学校在广场的北偏西30°的方向上，指的是以正北方向为始边向西旋转30°方向上。
图为
故C

此题考查的是位置与方向，掌握“上北下南，左西右东”的方向以及夹角的确定是关键。
11．B

根据题干，设今年有x人参加，则去年就是x-68人参加，则根据等量关系：去年参加的人数×3-4=今年参加的人数，据此列出方程解决问题。此题属于含有两个未知数的应用题，这类题用方程解答比较容易，关键是找准数量间的相等关系，设一个未知数为x，另一个未知数用含x的式子来表示，进而列并解方程即可。
【详解】
解：设今年有x人参加，则去年就是x﹣68人参加，根据题意可得方程：   
3（x-68）-4=x
3x-204-4=x    
2x=208     
x=104
答：今年有104人参加。
故选：B。
12．

【分析】
用这四个数分别与作差，得数最小的那个离最近。
【详解】
－＝
－＝
－＝
－＝
因为，所以最接近。

考查了异分母分数的加减法，先通分再计算。
13．99

【分析】
观察图形可知：前面和右面各有4个面露在外面，上面有3个面露在外面，所以共有4＋4＋3＝11个面露在外面，每个面的面积为3×3＝9平方分米，用9乘露在外面的面数11，即可求得露在外面的面积。
【详解】
露在外面的面共有：4＋4＋3＝11（个）
3×3×11＝99（平方分米）

此题考查规则图形的表面积，解决此题的关键是求出面露在外面的总个。
14．56

【分析】
将3个棱长是2厘米的正方体拼成一个长方体，则长方体的长是2×3＝6厘米，宽是2厘米，高是2厘米，带入表面积公式计算即可。
【详解】
（2×3×2＋2×3×2＋2×2）×2
＝（12＋12＋4）×2
＝28×2
＝56（平方厘米）

本题也可根据拼接后表面积比3个正方体的表面积减少4个正方形面的面积来解答。
15．               0.25##     375

【分析】
（1）求出18的的9，也就是求9是36的几分之几，则9÷36＝。
（2）2米和米都是带有单位的具体量，则比2米少米直接用2－＝米。
（3）1小时＝60分，15分转化成多少小时用除法。
（4）1千克＝1000克，千克转化成多少克用乘法。
【详解】
（1）18×＝9
9÷36＝
（2）2－＝（米）
（3）15÷60＝（时）
（4）×1000＝375（克）

注意把高级单位换算成低级单位，就乘单位间的进率，把低级单位换算成高级单位，就除以单位间进率。理解分数的意义是解第一空和第二空的关键。
16．8

【分析】
正方体棱长总和公式：棱长总和＝棱长×12，棱长＝棱长总和÷12，代入数据，求出正方体的棱长；再根据正方体体积公式：体积＝棱长×棱长×棱长，代入数据，即可解答。
【详解】
棱长：24÷12＝2（米）
体积：2×2×2
＝4×2
＝8（立方米）

熟练掌握和灵活运用正方体棱长公式、正方体体积公式是解答本题的关键。
17．48

【分析】
根据题意可知，下车的人数为12－3＝9（人），正好是车上原有人数的，用除法求出原有的人数，再加3即可。
【详解】
（12－3）÷＋3
＝9÷＋3
＝48（个）
这辆公交车上一共有48个座位。

此题主要考查了分数除法的应用，明确已知一个数的几分之几是多少，求这个数用除法，找出对应的数量是解题关键。
18．     东     45     9     西     70     8     东     40     5

【分析】
将方向和距离结合起来描述位置时，要注意三个要素：一是观测点，二是方向，三是距离。
【详解】
（1）学校在电影院的南偏东45°的方向上，距离电影院9千米。
（2）儿童书店在电影院北偏西70°的方向上，距离电影院8千米。
（3）超市在电影院北偏东40°的方向上，距离电影院5千米。

本题考查了根据方向和距离确定位置，在确定夹角时，要根据方向来确定，比如北偏东，就是把正北方向对应量角器上的0°刻度线。南偏东就是把正南方向对应量角器上的0°刻度线。
19．     40     37.5     一     40

【分析】
通过分析折线统计图，可以找出（1）、（3）题的数据信息。农机二厂2019年平均每季度的产值要用四个季度的产值和除以4。
【详解】
（1）一厂第二季度的产值是（40）万元。
（2）农机二厂2019年平均每季度的产值：
（10＋20＋50＋70）÷4
＝150÷4
＝37.5（万元）
（3）（一）厂三季度增长幅度最大，增长了80－40＝40（万元）

考查学生对复式折线统计图的认知情况。能利用统计图中的数据进行合理的分析，运用。
20．

【分析】
用单位“1”分别减去甲队和乙队修的占全长的分率即可。
【详解】
1－－
＝－
＝；
答：没修的占全部的。

熟练掌握异分母分数加减法的计算方法是解答本题的关键。
21．160厘米

【分析】
求木条的长度也就是求长方体的棱长总和，长方体的棱长总和＝（长＋宽＋高）×4，代入数据计算即可。
【详解】
（18＋12＋10）×4
＝40×4
＝160（厘米）
答：至少需要160厘米的木条。

此题考查了长方体棱长总和的相关应用，明确问题所求，牢记棱长总和计算公式是解题关键。
22．；

【分析】
（1）这个盒子用的铁皮的面积是这个长方形的面积减去4个边长为3厘米的小正方形的面积；
（2）做成长方体的长是（26－3×2）厘米，宽是（21－3×2）厘米；高是3厘米，由此依据长方体体积（容积）计算公式V＝abh求出容积。
【详解】
（1）26×21－3×3×4
＝546－36
＝510（平方厘米）
（2）（26－3×2）×（21－3×2）×3
＝（26－6）×（21－6）×3
＝20×15×3
＝900（立方厘米）
900立方厘米＝900毫升
答：这个盒子用了510平方厘米铁皮；它的容积是900毫升。

解决本题关键是找出长方体的长宽高和原来长方形的长和宽之间的关系，求出长宽高即可解决问题。
23．10公顷

【分析】
根据题目可知，这片地的种植水稻，单位“1”是这片地，单位“1”已知，用乘法，即50×＝30公顷，由于水稻面积中的种糯稻，单位“1”是水稻的面积，单位“1”已知，用乘法，即30×＝10公顷。
【详解】
50××
＝30×
＝10（公顷）
答：种糯稻10公顷。

本题主要考查分数乘法应用题，找准单位“1”，单位“1”已知，用乘法。
24．17.5dm3

【分析】
石块的体积等于水面上升的部分的体积；放入石块的水面后水面高度＝棱长－0.8，水面上升的高度＝放入石块后水面的高度－原来的水面的高度，进而求出这些石块的体积，据此解答。
【详解】
5×5×（5－0.8－3.5）
＝35×（4.2－3.5）
＝35×0.7
＝17.5（dm3）
答：这些石块的体积是17.5dm3。

利用求不规则物体体积的方法计算；找出水面上升高度是解题关键。
25．50箱

【分析】
设：购进梨子箱数是x箱，购进苹果的箱数是梨子箱数的，用梨子箱数×＝苹果的箱数，列方程：x＝40，解方程，即可解答。
【详解】
解：设水果店购进了x箱梨子。
x＝40
x＝40÷
x＝40×
x＝50
答：水果店购进了50想梨子。

本题考查求一个数的几分之几的问题，根据题意，列方程，解方程。
26．6分

【分析】
妈妈行驶的路程＋琪琪行驶的路程＝总路程，路程＝速度×时间，据此列方程解答。
【详解】
解：设经过x分相遇。
50x＋170x＝1320
220x＝1320
x＝6
答：经过6分相遇。

此题考查了相遇问题，等量关系较明显，分别表示出两人的路程是解题关键。
27．长颈鹿4.05米；鸵鸟2.25米

【分析】
设鸵鸟的身高是x米，则长颈鹿的身高是1.8x米，长颈鹿的身高－鸵鸟的升高＝1.8米，据此列方程解答即可。
【详解】
解：设设鸵鸟的身高是x米。
1.8x－x＝1.8
0.8x＝1.8
x＝2.25
1.8x＝2.25×1.8＝4.05
答：长颈鹿身高是4.05米，鸵鸟的身高是2.25米。

此题考查了列方程解决问题，分别表示出长颈鹿和鸵鸟的身高是解题关键。
















甘肃省酒泉市2022-2023学年五年级下学期数学期末调研
试卷（B卷）
一、填空题(共19分)
1．(本题2分)在括号里填上合适的单位。
一个粉笔盒的体积约为1( )；小轿车油箱的容积约为40( )。
2．(本题2分)比米少米是( )米；比千克多千克是( )千克。
3．(本题3分)( )        3.5升＝( )立方分米＝( )毫升
4．(本题4分)在括号里填上“＞”“＜”或“＝”。
÷6( )×       9÷( )9       
÷8( )16÷       ×( )÷
5．(本题2分)为了创建文明城市，施工队要对禹都大道一段长2千米的路面进行维护，如果每天修千米，( )天可以修完。
6．(本题2分)一件衣服按七折的售价是350元，这件衣服的原价是( )元。
7．(本题2分)4个棱长都是5cm的小正方体堆放在墙角处（如下图）。露在外面的面的面积一共是( )平方厘米。

8．(本题2分)把一根横截面积是40平方厘米，长是3米的方木截成三段，表面积增加了( )平方厘米。
二、判断题(共10分)
9．(本题2分)笑笑在淘气的南偏东40度方向．则淘气在笑笑的南偏西50度方向．    ( )
10．(本题2分)同学们参加“喜迎十四运”绘画展览，五年级一共去了264人，五年级去的人数比四年级的1.4倍少16人，设四年级去了x人，则可列方程为。( )
11．(本题2分)一盒糖，小峰取走了，小红取走余下的，两人取走的糖一样多。( )
12．(本题2分)如果一个长方体有四个面的面积相等，那么它的另外两个面是完全相同的正方形。( )
13．(本题2分)四（3）班同学做好事，第一天做好事30件，第二天上午做好事12件，下午做好事15件，四（3）班同学平均每天做好事的件数是（30＋12＋15）÷3＝19（件）。( )
三、选择题(共10分)
14．(本题2分)下列关于倒数的说法，错误的是（       ）。
A．1的倒数是1，0没有倒数
B．因为，所以和互为倒数
C．一个面积为1的长方形，它的长和宽互为倒数
D．因为，所以和互为倒数
15．(本题2分)在、、、、这些分数中，比大的有（       ）个。
A．2 B．3 C．4 D．5
16．(本题2分)对算式×5的理解错误的是（       ）。
A．把2平均分成7份取5份 B．的5倍是多少
C．5的是多少 D．把平均分成5份
17．(本题2分)棱长为1分米的正方体盒子中，最多可以放进（       ）个棱长为1厘米的小正方体。
A．10 B．100 C．1000 D．10000
18．(本题2分)铜管乐队有男生24人，________________，女生有多少人？根据算式，，横线上需要补的条件是（       ）。
A．男生人数相当于女生的 B．女生人数相当于男生的
C．男生人数相当于铜管乐队总人数的 D．女生人数相当于铜管乐队总人数的
四、计算题(共25分)
19．(本题4分)直接写得数。
　　　　　　　　　
　　　　　　　　　
20．(本题8分)用你喜欢的方法计算。
                    
                         
21．(本题9分)解方程。
x＝2                 x－＝                      5x－1.5x＝70
22．(本题4分)求下面图形的表面积和体积。（单位：）
（1） （2）
五、作图题(共6分)
23．(本题6分)笑笑从家沿东北方向走了200米到达学校，又从学校沿南偏东30°走了300米到达图书馆。请画图表示笑笑的行走过程。（请以1厘米代表100米）

六、解答题(共30分)
24．(本题6分)如图是南山区某超市毛衣、衬衫销售情况统计图。


（1）（       ）月份毛衣和衬衫的销售量相差最大，（       ）月份毛衣和衬衫的销售量相差最小。
（2）十二月份衬衫的销售量是毛衣的（       ）。
（3）七月份到十二月份，衬衫的销售量是怎样变化的？
25．(本题6分)（1）笑笑每天的睡眠时间约占一天时间的几分之几？是几小时？写下你的想法。
这是笑笑的每天时间安排。
学习
吃饭、娱乐和锻炼
睡眠时间
占一天时间的
约9小时
？

（2）你想给笑笑每天的时间安排提出什么建议？
26．(本题6分)在“深圳读书月”活动中，深圳书城科学类图书的销售量是3600册，是故事类图书销售量的，故事类图书的销售量是多少册？
27．(本题6分)公园里有杨树和柳树共87棵，杨树的棵数是柳树的2倍，杨树和柳树各有多少棵？（列方程解答）
28．(本题6分)如下图，现有空的长方体容器A和水深24厘米的长方体容器B。
（1）请你计算一下容器B中装了多少毫升水？


（2）如果将容器B中的水全部倒入容器A，容器A中的水深会是多少厘米？

答案：
1．     立方分米##dm3     升##L

【分析】
常见的体积单位有：立方米、立方分米、立方厘米等；常见的容积单位有：升、毫升等；根据数据的大小，选择合适的单位。
【详解】
一个粉笔盒的体积约为1立方分米；
小轿车油箱的容积约为40升。

联系生活实际，根据计量单位和数据的大小，灵活选择合适的计量单位。
2．         

【分析】
（1）根据题意，用－即可解答；
（2）根据题意，用＋即可解答。
【详解】
（1）－＝（米）
（2）＋＝（千克）

此题主要考查学生对异分母分数加减法的应用。
3．     800     3.5     3500

【分析】
1m3＝1000dm3；1升＝1立方分米；1升＝1000毫升；高级单位换算成低级单位，乘进率；低级单位换算成高级单位，除以进率，据此解答。
【详解】
m3＝800dm3
3.5升＝3.5立方分米＝3500毫升

解答本题的关键是熟记进率。
4．     ＝     ＜     ＜     ＞

【分析】
一个非0数，乘大于1的数，积大于原数；一个非0数，乘小于1的数，积小于原数；一个非0数，除以大于1的数，商小于被除数；一个非0数，除以小于1的数，商大于被除数，据此解答。
【详解】
÷6和×
因为÷6＝×；所以÷6＝×
9÷和9，因为＞1，所以9÷＜9
÷8和16÷
因为＜16，8＞1；＜1，所以÷8＜16÷
×和÷
因为＞1，所以×＞÷

根据积与乘数的关系、商与被除数的关系进行解答。
5．9

【分析】
根据公式可知：总长度÷每天修的长度＝时间，把数代入公式即可求解。
【详解】
2÷＝9（天）

本题主要考查分数的除法，熟练掌握分数除法的计算方法并灵活运用是解决本题的关键。
6．500

【分析】
打七折就是按原价的70%出售，把原价看作单位“1”，原价＝现价÷70%，据此解答。
【详解】
350÷70%＝500（元）

本题主要考查折扣问题，解题时要明确已知一个数的百分之几是多少，求这个数用除法。
7．250

【分析】
根据题意，从前面看，有3个面露在外面，从右面看有3个面露在外面；从上面看有3个面露在外面；从左面看还有1个，一共有3＋3＋3＋1个面露在外面；再根据：露在外面的面积＝棱长×棱长×露在外面正方形面的数量，代入数据，即可解答。
【详解】
露在外面的面：3＋3＋3＋1
＝9＋1
＝10（个）
5×5×10
＝25×10
＝250（平方厘米）

解答本题的关键是数清楚露在外面的面的个数，再进行解答。
8．160

【分析】
把一根横截面积是40平方厘米，长是3米的方木截成三段，锯了2次，则表面积就增加了2×2＝4个横截面的面积，用40乘4，列式解答即可。
【详解】
（3－1）×2×40
＝2×2×40
＝160（平方厘米）

解答本题的关键是依据长方体的切割特点：每切割一次，就增加2个底面积，求出增加了几个2个底面积即可。
9．╳

【详解】
略
10．√

【分析】
根据题目可知，五年级去的人数比四年级的1.4倍少16人，则五年级去的人数＝四年级去的人数×1.4－16；把x和五年级的人数代入等式，即可列式。
【详解】
根据分析可知，1.4x－16＝264
故√。

本题主要考查列方程，准确找到等量的关系。
11．×

【分析】
把这盒糖的总量看作单位“1”，小峰取走了，还剩下（1－），小红取走的是（1－）的，也就是（1－）×，与小峰取走的比较即可。
【详解】
（1－）×
＝
＝
＜，小峰取走的多。
故×

此题考查了分数乘法的相关应用，解答时注意单位“1”的变化。
12．√

【分析】
当长方体有相对的两个面是正方形时，其余四个面都是完全一样的长方形，反之，当长方体有四个面的面积相等，其余两个面一定是正方形，即可判断。
【详解】
当长方体有四个面的面积相等，说明这四个面的宽和长是一样的，一定有四条边相等，即其余两个面是正方形，所以原题说法正确。
故√

本题主要是利用长方体的面的特征：长方体有六个面，每个面都是长方形（特殊情况有相对的两个面是正方形）来解决问题。
13．×

【详解】
略
14．B

【分析】
根据倒数的定义：乘积是1的两个数互为倒数。据此逐项判断即可。
【详解】
A．1的倒数是1，0没有倒数，正确；
B．的倒数是8，的倒数是，所以和互为倒数是错误的；
C．面积为1的长方形，即长×宽＝1，所以它的长和宽互为倒数是正确的；
D．因为，所以和互为倒数，正确。
故B

本题主要考查倒数的认识。注意：1的倒数是1，0没有倒数。
15．A

【分析】
比较分子大于分母的一半时分数大于；分子小于分母的一半时分数小于；分子等于分母的一半时分数等于，据此解答。
【详解】
根据分析可知，＞；＜；＞；＜；＜
比大的分数有和，共2个。
故答案选：A

本题主要考查分数的大小比较，理解分数的意义可以快速解答。
16．D

【分析】
分析每个选项，找出错误的一项即可。
【详解】
A．把2平均分成7份，每份是，取其中的5份，就是5个，用算式×5来表示。
B．求一个数的几倍是多少，用乘法。所以求的5倍是多少，用算式×5来表示。
C．求一个数的几分之几是多少，用乘法，所以求5的是多少，用算式×5来表示       
D. 把平均分成5份，用算式÷5来表示。
故D

此题主要考查分数乘法的计算，分数乘整数，表示几个相同分数相加，或求一个数的几分之几。
17．C

【分析】
根据正方体体积公式：棱长×棱长×棱长，代入数据，求出棱长1分米的正方体的体积和棱长1厘米的正方体体积，再用大正方体的体积÷小正方体的体积，即可解答。
【详解】
1分米＝10厘米
10×10×10÷（1×1×1）
＝100×10÷（1×1）
＝1000÷1
＝1000（个）
故C

利用正方体体积公式进行解答，注意单位名数的统一。
18．A

【分析】
根据24÷，把女生人数看作单位“1”，男生人数相当于女生的，根据已知一个数的几分之几是多少，求这个数用除法，利用算式24÷求出女生的人数。
【详解】
男生人数相当于女生的
24÷＝36（人）
故A

解决此问题关键确定单位”1“是谁，根据单位”1“已知用乘法，未知用除法。
19．；；3；6
0；；13；0.16

【详解】
略
20．11；24；
；

【分析】
根据乘法分配律进行简算；
根据乘法分配律进行简算；
先将除法变为乘法，再根据乘法交换律进行简算；
根据减法的性质进行简算。
【详解】

＝
＝3＋8
＝11

＝
＝
＝24

＝
＝
＝

＝
＝
＝
21．x＝3；x＝；x＝20

【分析】
x＝2，根据等式的性质2，方程两边同时除以即可；
x－＝，根据等式的性质1，方程两边同时加上即可；
5x－1.5x＝70，先计算出5－1.5的差，再根据等式的性质2，方程两边同时除以5－1.5的差即可。
【详解】
x＝2
解：x÷＝2÷
x＝2×
x＝3
x－＝
解：x－＋＝＋
x＝
5x－1.5x＝70
解：3.5x＝70
3.5x÷3.5＝70÷3.5
x＝20
22．（1）表面积：112cm2；体积：64cm3；
（2）表面积：114cm2；体积：55cm3

【分析】
（1）长方体的变面积＝（长×宽＋长×高＋宽×高）×2；长方体的体积＝长×宽×高；代入数据计算即可求出表面积和体积；
（2）由图可知：组合体的表面积＝长方体的表面积＋正方体前后左右四个面的面积，代入数据计算即可；组合体的体积＝长方体的体积＋正方体的体积，代入数据计算即可。
【详解】
（1）表面积：（8×4＋8×2＋4×2）×2
＝（32＋16＋8）×2
＝56×2
＝112（cm2）
体积：8×4×2
＝32×2
＝64（cm3）
（2）表面积：（7×4＋7×1＋4×1）×2＋3×3×4
＝（28＋7＋4）×2＋9×4
＝39×2＋36
＝114（cm2）
体积：7×4×1＋3×3×3
＝28＋27
＝55（cm3）
23．见详解

【分析】
根据图上距离和比例尺，分别计算各点之间的图上距离，然后利用图上确定方向的方法，结合题目所给信息，完成作图。
【详解】
200÷100＝2（厘米）
300÷100＝3（厘米）
笑笑所走线路图如下：



此题主要考查依据方向（角度）和距离判定物体位置及画线路图的方法。
24．（1）七；十；（2）；（3）销售量是一直在下降

【分析】
（1）根据统计图中的数据可知几月份毛衣和衬衫的销售量相差最大，几月份毛衣和衬衫的销售量相差最小；
（2）根据统计图中的数据可以得到十二月份衬衫和毛衣的销售量，从而可以得到十二月份衬衫的销售量是毛衣的几分之几；
（3）根据统计图中的数据可以得到七月份到十二月份，衬衫的销售量是怎样变化的。
【详解】
（（1）由统计图可知，七月份毛衣和衬衫的销售量相差最大，十月份毛衣和衬衫的销售量相差最小；
（2）因为十二月份衬衫的销售量是400件，毛衣的销售量是800件，所以十二月份衬衫的销售量是毛衣的：400÷800＝；
（3）由统计图可知，七月份到十二月份，衬衫的销售量是一直在下降。

此题考查复式折线统计图，由问题从统计图中获取相关信息是解答本题的关键，用到的数学思想是数形结合的思想。
25．（1）；7小时
（2）见详解（答案不唯一）

【分析】
（1）一天有24小时，笑笑吃饭、娱乐和锻炼的时间约9小时，用9除以24即可求出她吃饭、娱乐和锻炼的时间占一天时间的几分之几。把一天时间看作单位“1”，用1减去笑笑学习、吃饭、娱乐和锻炼所占的分率即是她每天的睡眠时间约占一天时间的几分之几。用24乘这个分数即可求出是几小时。
（2）小学生每天的睡眠时间应是9到10个小时，笑笑睡眠时间不足，建议增加睡眠时间。
【详解】
（1）9÷24＝
1－－＝
24×＝7（小时）
答：笑笑每天的睡眠时间约占一天时间的，是7小时。
（2）小学生每天的睡眠时间应是9到10个小时。为了健康，建议笑笑合理安排，增加睡眠时间。（答案不唯一）

求一个数是另一个数的几分之几，用除法计算；求一个数的几分之几是多少，用乘法计算。
26．5760册

【分析】
把故事类图书销售量看作单位“1”，单位“1”未知，则用科学类图书销售量除以，即可求出故事类图书的销售量。
【详解】
3600÷
＝3600×
＝5760（册）
答：故事类图书的销售量是5760册。

本题考查分数除法的应用，根据题干信息找准单位“1”是解决本题的关键。
27．杨树：58棵；柳树：29棵

【分析】
设柳树有x棵，杨树是柳树的2倍，则柳树有2x棵，杨树和柳树共87棵，列方程：x＋2x＝87，解方程，即可解答。
【详解】
解：设柳树有x棵，则杨树有2x棵。
x＋2x＝87
3x＝87
x＝87÷3
x＝29
杨树有：29×2＝58（棵）
答：杨树有58棵，柳树有29棵。

根据方程的实际应用，利用杨树与柳树之间的倍数关系，设出未知数，找出相关的量，列方程，解方程。
28．（1）14400毫升
（2）12厘米

【分析】
（1）根据长方体的体积公式：体积＝长×宽×高，长是30厘米，宽是20厘米，高是24厘米，代入数据，即可解答。
（2）由于体积不变，水倒入容器A中，求水深，用水的体积除以容器B的底面积，代入数据，即可解答。
【详解】
（1）30×20×24
＝600×24
＝14400（立方厘米）
14400立方厘米＝14400毫升
答：容器B中装14400毫升水。
（2）14400÷（40×30）
＝14400÷1200
＝12（厘米）
答：容器A中水深会是12厘米。

利用长方体体积公式进行解答；关键明确容器B中的水倒入容器A中，水的体积不变。