2022-2023学年天津二十中九年级（上）期末数学试卷

这是一份2022-2023学年天津二十中九年级（上）期末数学试卷，共29页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年天津二十中九年级（上）期末数学试卷
一、选择题
1．下列图形中，是中心对称图形的是（　　）
A． B．
C． D．
2．下列关于抛物线y＝（x+2）2+6的说法，正确的是（　　）
A．抛物线开口向下
B．抛物线的顶点坐标为（2，6）
C．抛物线的对称轴是直线x＝6
D．抛物线经过点（0，10）
3．如图，已知AB是⊙O的直径，CD是弦，若∠BCD＝24°，则∠ABD＝（　　）

A．54° B．56° C．64° D．66°
4．如图，△ABC中，点D、E分别在AB、AC边上，则下列条件中，不一定能使△AED∽△ABC的是（　　）

A．∠2＝∠B B．∠1＝∠C C． D．
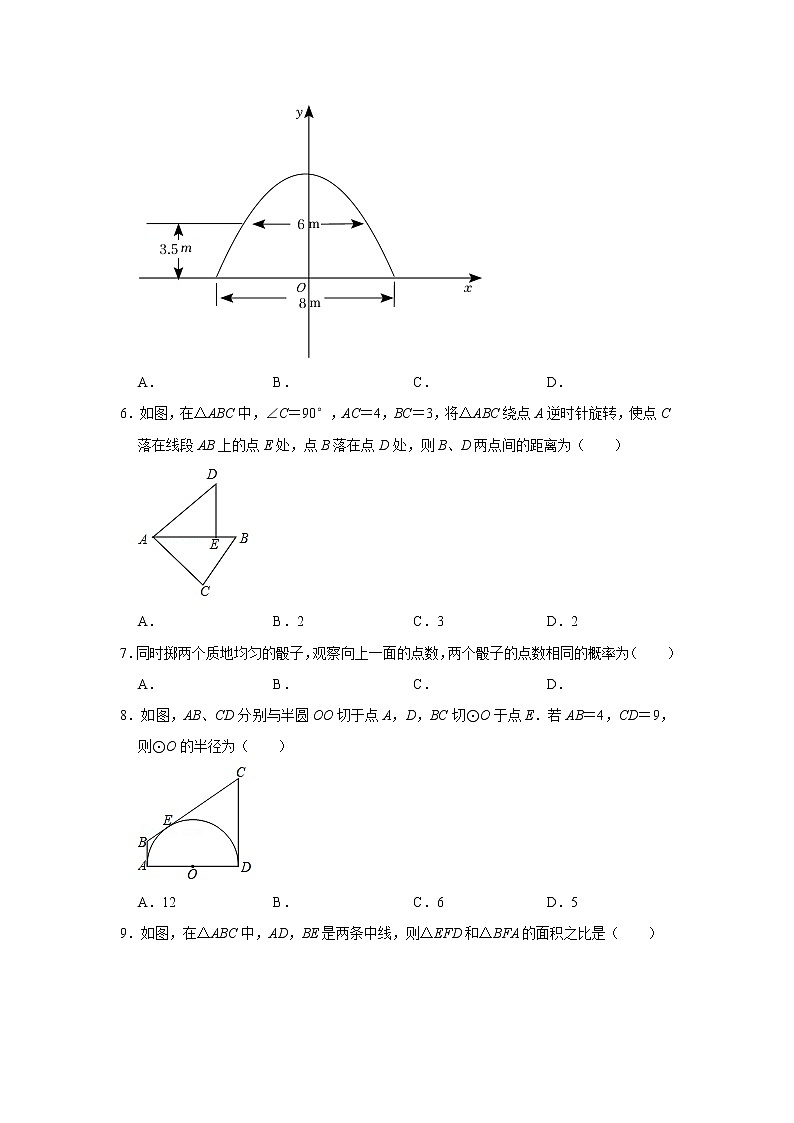
5．如图，某大门的形状是一抛物线形建筑，大门的地面宽8m，在两侧距地面3.5m高处有两个挂单位名牌匾用的铁环，两铁环的水平距离是6m..若按图所示建立平面直角坐标系，则抛物线的解析式是（　　）（建筑物厚度忽略不计）

A． B． C． D．
6．如图，在△ABC中，∠C＝90°，AC＝4，BC＝3，将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则B、D两点间的距离为（　　）

A． B．2 C．3 D．2
7．同时掷两个质地均匀的骰子，观察向上一面的点数，两个骰子的点数相同的概率为（　　）
A． B． C． D．
8．如图，AB、CD分别与半圆OO切于点A，D，BC切⊙O于点E．若AB＝4，CD＝9，则⊙O的半径为（　　）

A．12 B． C．6 D．5
9．如图，在△ABC中，AD，BE是两条中线，则△EFD和△BFA的面积之比是（　　）

A．1：2 B．1：4 C．1：3 D．2：3
10．二次函数y＝x2﹣6x+5配成顶点式正确的是（　　），顶点坐标为（　　）
A．y＝（x﹣3）2﹣4；（3，﹣4） B．y＝（x+3）2﹣4；（﹣3，﹣4）
C．y＝（x+3）2+5；（﹣3，5） D．y＝（x﹣3）2+14；（3，14）
11．如图，在平面直角坐标系中，已知点A（﹣3，6）、B（﹣9，﹣3），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（　　）

A．（﹣1，2） B．（﹣9，18）
C．（﹣9，18）或（9，﹣18） D．（﹣1，2）或（1，﹣2）
12．已知抛物线y＝ax2+bx+c（a，b，c是常数，a≠0）经过点（﹣1，﹣1），（0，1），当x＝﹣2时，与其对应的函数值y＞1．有下列结论：
①abc＞0；
②关于x的方程ax2+bx+c﹣3＝0有两个不等的实数根；
③a+b+c＞7．
其中，正确结论的个数是（　　）
A．0 B．1 C．2 D．3
二、填空题
13．已知正六边形的半径是4，则这个正六边形的周长为　 　．
14．两个正四面体骰子的各面上分别标明数字1，2，3，4，如同时投掷这两个正四面体骰子，则着地的面所得的点数之和等于5的概率为　 　．
15．若扇形的圆心角为90°，半径为6，则该扇形的弧长为　 　．
16．如果A（a1，b1），B（a2，b2）两点在反比例函数y图象的同一支上，且a1＜a2，那么b1　 　b2．
17．如图，在矩形ABCD中，∠B的平分线BE与AD交于点E，∠BED的平分线EF与DC交于点F，若AB＝9，DF＝2FC，则BC＝　 　．（结果保留根号）

18．在如图所示的网格中，每个小正方形的边长都为1，⊙O是△ABC的外接圆，点A，B均为格点，点C是小正方形一边的中点．
（Ⅰ）线段AB的长度等于 　 　；
（Ⅱ）请借助无刻度的直尺，在给定的网格中先确定圆心O，再作∠BAC的平分线AP交⊙O于点P．在下面的横线上简要说明点O和点P的位置是如何找到的．
　 　．

三、解答题（本大题共8小题。解答应写出文字说明、演算步骤或推理过程）
19．解方程：x2+4x﹣1＝0．
20．已知：关于x的一元二次方程2x2﹣3x+k＝0有两个不相等的实数根．求k的取值范围．
21．已知，⊙O中，，D是⊙O上的点，OC⊥BD．
（1）如图①，求证；
（2）如图②，连接AB，BC，CD，DA，若∠A＝70°，求∠BCD，∠ADB的大小．
22．如图，已知等边△ABC中，AB＝12．以AB为直径的半⊙O与边AC相交于点D．过点D作DE⊥BC，垂足为E；过点E作EF⊥AB，垂足为F，连接DF．
（1）求证：DE是⊙O的切线；
（2）求EF的长．

23．某种品牌的手机经过四、五月份连续两次降价，每部售价由2500元降到了1600元．求平均每月降价的百分率．
24．商城某种商品平均每天可销售20件，每件获得利润40元，为庆元旦，决定对该商品进行促销活动，经调查发现，该商品每件每降价1元，平均每天可多售出2件．设该商品每件降价x元，请解答下列问题：
（Ⅰ）用含x的代数式表示：①降价后每售一件该商品获得利润 　 　元；②降价后平均每天售出 　 　件该商品；
（Ⅱ）在此次促销活动中，商城若要获得最大利润，每件该商品应降价多少元？此时每天获得最大利润为多少元？
25．如图乙，△ABC和△ADE是有公共顶点的等腰直角三角形，∠BAC＝∠DAE＝90°，点P为射线BD，CE的交点．

（1）如图甲，将△ADE绕点A旋转，当C、D、E在同一条直线上时，连接BD、BE，求证：BD＝CE；
（2）若AB＝6，AD＝3，把△ADE绕点A旋转：
①当∠CAE＝90°时，求PB的长；
②若M为线段BC中点，直接写出旋转过程中线段DM长的最大值．
26．如图，已知抛物线y＝x2+bx+c的图象与x轴的一个交点为B（5，0），另一个交点A，且与y轴交于点C（0，5）．
（1）求直线BC与抛物线的解析式．
（2）若点M是抛物线在x轴下方图象上的一动点，过点M作MN∥y轴交BC于点N，求MN的最大值．
（3）在（2）的条件下，MN取得最大值时，若点P是抛物线在x轴下方图象上任意一点，以BC为边作平行四边形CBPQ，设平行四边形CBPQ的面积为S1，△ABN的面积为S2，且S1＝6S2，求点P的坐标．


2022-2023学年天津二十中九年级（上）期末数学试卷
参考答案与试题解析
一、选择题
1．下列图形中，是中心对称图形的是（　　）
A． B．
C． D．
【分析】根据中心对称图形的定义进行判断，即可得出答案．
【解答】解：A．不是中心对称图形，故本选项不符合题意；
B．不是中心对称图形，故本选项不符合题意；
C．是中心对称图形，故本选项符合题意；
D．不是中心对称图形，故本选项不符合题意．
故选：C．
【点评】本题考查了中心对称图形的概念，判断中心对称图形是要寻找对称中心，旋转180度后与原图重合．
2．下列关于抛物线y＝（x+2）2+6的说法，正确的是（　　）
A．抛物线开口向下
B．抛物线的顶点坐标为（2，6）
C．抛物线的对称轴是直线x＝6
D．抛物线经过点（0，10）
【分析】根据抛物线的解析式可以判断各个选项中的结论是否正确，从而可以解答本题．
【解答】解：∵y＝（x+2）2+6＝x2+4x+10，
∴a＝1，该抛物线的开口向上，故选项A错误，
抛物线的顶点坐标是（﹣2，6），故选项B错误，
抛物线的对称轴是直线x＝﹣2，故选项C错误，
当x＝0时，y＝10，故选项D正确，
故选：D．
【点评】本题考查二次函数的性质，解答本题的关键是明确题意，利用二次函数的性质解答．
3．如图，已知AB是⊙O的直径，CD是弦，若∠BCD＝24°，则∠ABD＝（　　）

A．54° B．56° C．64° D．66°
【分析】根据圆周角定理得到∠ADB＝90°，∠A＝∠BCD＝24°，然后利用互余计算∠ABD的度数．
【解答】解：∵AB是⊙O的直径，
∴∠ADB＝90°，
∵∠A＝∠BCD＝24°，
∴∠ABD＝90°﹣∠A＝90°﹣24°＝66°．
故选：D．
【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．
4．如图，△ABC中，点D、E分别在AB、AC边上，则下列条件中，不一定能使△AED∽△ABC的是（　　）

A．∠2＝∠B B．∠1＝∠C C． D．
【分析】相似三角形的判定：
（1）三边法：三组对应边的比相等的两个三角形相似；
（2）两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；
（3）两角法：有两组角对应相等的两个三角形相似．
由此结合各选项进行判断即可．
【解答】解：∠A＝∠A，
A、若添加∠2＝∠B，可利用两角法判定△AED∽△ABC，故本选项错误；
B、若添加∠1＝∠C，可利用两角法判定△AED∽△ABC，故本选项错误；
C、若添加，可利用两边及其夹角法判定△AED∽△ABC，故本选项错误；
D、若添加，不能判定△AED∽△ABC，故本选项正确；
故选：D．
【点评】本题考查了相似三角形的判定，解答本题的关键是熟练掌握相似三角形的判定定理，难度一般．
5．如图，某大门的形状是一抛物线形建筑，大门的地面宽8m，在两侧距地面3.5m高处有两个挂单位名牌匾用的铁环，两铁环的水平距离是6m..若按图所示建立平面直角坐标系，则抛物线的解析式是（　　）（建筑物厚度忽略不计）

A． B． C． D．
【分析】设出函数解析式，把（4，0）和（3，3.5）代入抛物线，用待定系数法求函数解析式即可．
【解答】解：根据题意，抛物线过（﹣4，0）、（4，0）、（﹣3，3.5）、（3、3.5）四点，
∵对称轴是y轴，
∴b＝0，
设抛物线解析式为y＝ax2+c，
把（4，0）和（3，3.5）代入抛物线得：
，
解得：，
∴抛物线解析式为yx2+8，
故选：A．
【点评】本题考查二次函数的实际应用，解题的关键是掌握待定系数法．
6．如图，在△ABC中，∠C＝90°，AC＝4，BC＝3，将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则B、D两点间的距离为（　　）

A． B．2 C．3 D．2
【分析】通过勾股定理计算出AB长度，利用旋转性质求出各对应线段长度，利用勾股定理求出B、D两点间的距离．
【解答】解：连接BD．

∵在△ABC中，∠C＝90°，AC＝4，BC＝3，
∴AB＝5，
∵将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，
∴AE＝4，DE＝3，
∴BE＝1，
在Rt△BED中，
BD．
故选：A．
【点评】题目考查勾股定理和旋转的基本性质，解决此类问题的关键是掌握旋转的基本性质，特别是线段之间的关系．题目整体较为简单，适合随堂训练．
7．同时掷两个质地均匀的骰子，观察向上一面的点数，两个骰子的点数相同的概率为（　　）
A． B． C． D．
【分析】画树状图，共有36种等可能的结果，其中两个骰子的点数相同的结果有6种，再由概率公式求解即可．
【解答】解：画树状图如下：

共有36种等可能的结果，其中两个骰子的点数相同的结果有6种，
∴两个骰子的点数相同的概率为，
故选：C．
【点评】本题考查了树状图法求概率，树状图法可以不重复不遗漏的列出所有可能的结果，适用于两步或两步以上完成的事件．解题时还要注意是放回试验还是不放回试验．用到的知识点为：概率＝所求情况数与总情况数之比．
8．如图，AB、CD分别与半圆OO切于点A，D，BC切⊙O于点E．若AB＝4，CD＝9，则⊙O的半径为（　　）

A．12 B． C．6 D．5
【分析】过B作CD的垂线，设垂足为F，由切线长定理知：BA＝BE，CE＝CD；即BC＝AB+CD，在构建的Rt△BFC中，BC＝AB+CD，CF＝CD﹣AB，根据勾股定理即可求出BF即圆的直径，进而可求出⊙O的半径．
【解答】解：过B作BF⊥CD于F，
∵AB、CD与半圆O切于A、D，
∴∠BAD＝∠CDA＝∠BFD＝90°，
∴四边形ADFB为矩形，
∴AB＝DF，BF＝AD，
∵AB＝BE＝4，CD＝CE＝9，
∴BC＝BE+CE＝13，
∵AB、CD与半圆O相切，
∴四边形ADFB为矩形，
∴CF＝CD﹣FD＝9﹣4＝5，
在Rt△BFC中，BF12，
∴AD＝BF＝12，
∴⊙O的半径为6．
故选：C．

【点评】本题考查切线的性质、勾股定理、矩形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造特殊四边形解决问题．
9．如图，在△ABC中，AD，BE是两条中线，则△EFD和△BFA的面积之比是（　　）

A．1：2 B．1：4 C．1：3 D．2：3
【分析】利用三角形的中位线定理可得DE：AB＝1：2，再利用相似三角形的性质即可解决问题．
【解答】解：∵CE＝AE，CD＝DB，
∴ED∥AB，DEAB，
∴△DEF∽△ABF，
∴（）2，
故选：B．
【点评】本题考查三角形的面积，三角形的中位线定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
10．二次函数y＝x2﹣6x+5配成顶点式正确的是（　　），顶点坐标为（　　）
A．y＝（x﹣3）2﹣4；（3，﹣4） B．y＝（x+3）2﹣4；（﹣3，﹣4）
C．y＝（x+3）2+5；（﹣3，5） D．y＝（x﹣3）2+14；（3，14）
【分析】根据二次函数的解析式，可以将该函数解析式化为顶点式，从而可以解答本题．
【解答】解：∵二次函数y＝x2﹣6x+5＝（x﹣3）2﹣4，
所以该函数的顶点坐标是（3，﹣4），
故选：A．
【点评】本题考查二次函数的性质、二次函数的三种形式，解答本题的关键是明确题意，利用二次函数的性质解答．
11．如图，在平面直角坐标系中，已知点A（﹣3，6）、B（﹣9，﹣3），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（　　）

A．（﹣1，2） B．（﹣9，18）
C．（﹣9，18）或（9，﹣18） D．（﹣1，2）或（1，﹣2）
【分析】根据在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k解答．
【解答】解：∵点A（﹣3，6），以原点O为位似中心，相似比为，把△ABO缩小，
∴点A的对应点A′的坐标是（﹣1，2）或（1，﹣2），
故选：D．
【点评】本题考查的是位似变换的概念和性质，在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k．
12．已知抛物线y＝ax2+bx+c（a，b，c是常数，a≠0）经过点（﹣1，﹣1），（0，1），当x＝﹣2时，与其对应的函数值y＞1．有下列结论：
①abc＞0；
②关于x的方程ax2+bx+c﹣3＝0有两个不等的实数根；
③a+b+c＞7．
其中，正确结论的个数是（　　）
A．0 B．1 C．2 D．3
【分析】①当x＝0时，c＝1，由点（﹣1，﹣1）得a＝b﹣2，由x＝﹣2时，与其对应的函数值y＞1可得b＞4，进而得出abc＞0；
②将a＝b﹣2，c＝1代入方程，根据根的判别式即可判断；
③将a＝b﹣2，c＝1代入a+b+c，求解后即可判断．
【解答】解：①∵抛物线y＝ax2+bx+c（a，b，c是常数，a≠0）经过点（﹣1，﹣1），（0，1），
∴c＝1，a﹣b+c＝﹣1，
∴a＝b﹣2，
∵当x＝﹣2时，与其对应的函数值y＞1．
∴4a﹣2b+1＞1，
∴4（b﹣2）﹣2b+1＞1，解得：b＞4，
∴a＝b﹣2＞0，
∴abc＞0，故①正确；
②∵a＝b﹣2，c＝1，
∴（b﹣2）x2+bx+1﹣3＝0，即（b﹣2）x2+bx﹣2＝0，
∴Δ＝b2﹣4×（﹣2）×（b﹣2）＝b2+8b﹣16＝b（b+8）﹣16，
∵b＞4，
∴Δ＞0，
∴关于x的方程ax2+bx+c﹣3＝0有两个不等的实数根，故②正确；
③∵a＝b﹣2，c＝1，
∴a+b+c＝b﹣2+b+1＝2b﹣1，
∵b＞4，
∴2b﹣1＞7，
∴a+b+c＞7．
故③正确；
故选：D．
【点评】本题考查二次函数的图象与性质，根的判别式；熟练掌握二次函数图象上点的特征，逐一分析三条结论的正误是解题的关键．
二、填空题
13．已知正六边形的半径是4，则这个正六边形的周长为　24　．
【分析】根据正六边形的半径可求出其边长为4，进而可求出它的周长．
【解答】解：正六边形的半径为4，则边长是4，因而周长是4×6＝24．
故答案为：24．
【点评】此题主要考查了正多边形和圆的有关计算，正六边形的半径与边长相等是需要熟记的内容．
14．两个正四面体骰子的各面上分别标明数字1，2，3，4，如同时投掷这两个正四面体骰子，则着地的面所得的点数之和等于5的概率为　　．
【分析】首先列出表格，由表格求得所有等可能的出现结果与着地的面所得的点数之和等于5的情况，然后根据概率公式求出该事件的概率．
【解答】解：列表得：

1
2
3
4
1
1+1＝2
2+1＝3
3+1＝4
4+1＝5
2
1+2＝3
2+2＝4
3+2＝5
4+2＝6
3
1+3＝4
2+3＝5
3+3＝6
4+3＝7
4
1+4＝5
2+4＝6
3+4＝7
4+4＝8
∵一共有16种情况，着地的面所得的点数之和等于5的有4种，
∴着地的面所得的点数之和等于5的概率为：．
故答案为：．
【点评】本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．用到的知识点为：概率＝所求情况数与总情况数之比．
15．若扇形的圆心角为90°，半径为6，则该扇形的弧长为　3π　．
【分析】根据弧长公式计算．
【解答】解：该扇形的弧长3π．
故答案为：3π．
【点评】本题考查了弧长的计算：弧长公式：l（弧长为l，圆心角度数为n，圆的半径为R）．
16．如果A（a1，b1），B（a2，b2）两点在反比例函数y图象的同一支上，且a1＜a2，那么b1　＜　b2．
【分析】根据k＝﹣2＜0，在每个象限内，y随x的增大而增大，即可得出答案．
【解答】解：∵k＝﹣2＜0，
∴在每个象限内，y随x的增大而增大，
∵A（a1，b1），B（a2，b2）两点在该反比例函数图象的同一支上，a1＜a2，
∴b1＜b2，
故答案为：＜．
【点评】本题考查了反比例函数图象上点的坐标特征，反比例函数的性质的应用，注意：反比例函数y（k≠0，k为常数），当k＞0时，在每个象限内，y随x的增大而减小，当k＜0时，在每个象限内，y随x的增大而增大．
17．如图，在矩形ABCD中，∠B的平分线BE与AD交于点E，∠BED的平分线EF与DC交于点F，若AB＝9，DF＝2FC，则BC＝　　．（结果保留根号）

【分析】先延长EF和BC，交于点G，再根据条件可以判断三角形ABE为等腰直角三角形，并求得其斜边BE的长，然后根据条件判断三角形BEG为等腰三角形，最后根据△EFD∽△GFC得出CG与DE的倍数关系，并根据BG＝BC+CG进行计算即可．
【解答】解：延长EF和BC，交于点G
∵矩形ABCD中，∠B的角平分线BE与AD交于点E，
∴∠ABE＝∠AEB＝45°，
∴AB＝AE＝9，
∴直角三角形ABE中，BE，
又∵∠BED的角平分线EF与DC交于点F，
∴∠BEG＝∠DEF
∵AD∥BC
∴∠G＝∠DEF
∴∠BEG＝∠G
∴BG＝BE
由∠G＝∠DEF，∠EFD＝∠GFC，可得△EFD∽△GFC
∴
设CG＝x，DE＝2x，则AD＝9+2x＝BC
∵BG＝BC+CG
∴9+2x+x
解得x
∴BC＝9+2（3）
故答案为：

【点评】本题主要考查了矩形、相似三角形以及等腰三角形，解决问题的关键是掌握矩形的性质：矩形的四个角都是直角，矩形的对边相等．解题时注意：有两个角对应相等的两个三角形相似．
18．在如图所示的网格中，每个小正方形的边长都为1，⊙O是△ABC的外接圆，点A，B均为格点，点C是小正方形一边的中点．
（Ⅰ）线段AB的长度等于 　　；
（Ⅱ）请借助无刻度的直尺，在给定的网格中先确定圆心O，再作∠BAC的平分线AP交⊙O于点P．在下面的横线上简要说明点O和点P的位置是如何找到的．
　作直径CQ，MN交于点O，点O即为圆心，作∠ARB的角平分线RT交⊙O于点P，作射线OP即可　．

【分析】（Ⅰ）利用勾股定理求解；
（Ⅱ）作直径CQ，MN交于点O，点O即为圆心，作∠ARB的角平分线RT交⊙O于点P，作射线OP即可．
【解答】解：（Ⅰ）如图，AB．
故答案为：．

（Ⅱ）如图，点O，射线OP即为所求．
方法：作直径CQ，MN交于点O，点O即为圆心，作∠ARB的角平分线RT交⊙O于点P，作射线OP即可．
故答案为：作直径CQ，MN交于点O，点O即为圆心，作∠ARB的角平分线RT交⊙O于点P，作射线OP即可．
【点评】本题考查作图﹣复杂作图，圆周角定理，三角形的外心，勾股定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
三、解答题（本大题共8小题。解答应写出文字说明、演算步骤或推理过程）
19．解方程：x2+4x﹣1＝0．
【分析】首先进行移项，得到x2+4x＝1，方程左右两边同时加上4，则方程左边就是完全平方式，右边是常数的形式，再利用直接开平方法即可求解．
【解答】解：∵x2+4x﹣1＝0
∴x2+4x＝1
∴x2+4x+4＝1+4
∴（x+2）2＝5
∴x＝﹣2±
∴x1＝﹣2，x2＝﹣2．
【点评】配方法的一般步骤：
（1）把常数项移到等号的右边；
（2）把二次项的系数化为1；
（3）等式两边同时加上一次项系数一半的平方．
选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
20．已知：关于x的一元二次方程2x2﹣3x+k＝0有两个不相等的实数根．求k的取值范围．
【分析】根据一元二次方程的定义和△的意义得到k≠0且Δ＞0，即（﹣3）2﹣4×k×2＞0，然后解不等式即可得到k的取值范围．
【解答】解：根据题意知Δ＝（﹣3）2﹣4×k×2＞0，
解得：k，
∴k的取值范围是k．
【点评】本题考查了一元二次方程ax2+bx+c＝0（a≠0）的根的判别式Δ＝b2﹣4ac：当Δ＞0，方程有两个不相等的实数根；当Δ＝0，方程有两个相等的实数根；当Δ＜0，方程没有实数根．也考查了一元二次方程的定义．
21．已知，⊙O中，，D是⊙O上的点，OC⊥BD．
（1）如图①，求证；
（2）如图②，连接AB，BC，CD，DA，若∠A＝70°，求∠BCD，∠ADB的大小．
【分析】（1）根据垂径定理求出，再根据已知条件得出答案即可；
（2）根据圆内接四边形的性质求出∠BCD，求出∠CBD＝∠CDB＝35°，再求出∠ADB即可．
【解答】（1）证明：∵OC⊥BD，OC过O，
∴，
∵，
∴；

（2）解：∵四边形ABCD是圆内接四边形，
∴∠A+∠BCD＝180°，
∵∠A＝70°，
∴∠BCD＝110°，
∵，
∴∠CBD＝∠CDB（180°﹣∠BCD）＝35°，
∵，
∴∠ADB＝∠CDB＝35°．
【点评】本题考查了圆内接四边形的性质，等腰三角形的性质，垂径定理，圆周角定理，圆心角、弧、弦之间的关系等知识点，能综合运用知识点进行推理是解此题的关键．
22．如图，已知等边△ABC中，AB＝12．以AB为直径的半⊙O与边AC相交于点D．过点D作DE⊥BC，垂足为E；过点E作EF⊥AB，垂足为F，连接DF．
（1）求证：DE是⊙O的切线；
（2）求EF的长．

【分析】（1）连接OD，证明OD∥BC，根据平行线的性质得到DE⊥OD，根据切线的判定定理证明结论；
（2）求出CD＝6，进而求出CE，即可求出BE，根据正弦的定义求出EF．
【解答】（1）证明：连接OD，
∵△ABC为等边三角形，
∴∠A＝∠C，
∵OA＝OD，
∴∠A＝∠ODA，
∴∠ODA＝∠C，
∴OD∥BC，
∵DE⊥BC，
∴DE⊥OD，
∵OD是⊙O的半径，
∴DE是⊙O的切线；
（2）解：由（1）知，OD∥BC，
∵OA＝OB，
∴AD＝CD，
∵AC＝12，
∴CD＝6，
在Rt△CDE中，∠C＝60°，
∴∠CDE＝30°，
∴CECD＝3，
∴BE＝BC﹣CE＝9，
在Rt△BEF中，∠B＝60°，
∴EF＝BE•sinB＝9．

【点评】本题考查了等边三角形的性质和判定、切线的判定、勾股定理、含30度角的直角三角形的性质、锐角三角函数，正确作出辅助线是解本题的关键．
23．某种品牌的手机经过四、五月份连续两次降价，每部售价由2500元降到了1600元．求平均每月降价的百分率．
【分析】本题可根据：原售价×（1﹣降低率）2＝降低后的售价，然后列出方程求解即可．
【解答】解：设平均降价x元，依题意得：2500（1﹣x）2＝1600，
化简得：（1﹣x）2，
解得：x＝0.2＝20%或x＝1.8（舍去），
答：平均每月降价的百分率为20%．
【点评】本题考查降低率的问题，解题关键是根据原售价×（1﹣降低率）2＝降低后的售价列出方程，难度一般．
24．商城某种商品平均每天可销售20件，每件获得利润40元，为庆元旦，决定对该商品进行促销活动，经调查发现，该商品每件每降价1元，平均每天可多售出2件．设该商品每件降价x元，请解答下列问题：
（Ⅰ）用含x的代数式表示：①降价后每售一件该商品获得利润 　（40﹣x）　元；②降价后平均每天售出 　（20+2x）　件该商品；
（Ⅱ）在此次促销活动中，商城若要获得最大利润，每件该商品应降价多少元？此时每天获得最大利润为多少元？
【分析】（Ⅰ）①用原来价格减去降低的价格即可；②用原销售量加上因降价而增加的销售量即可；
（Ⅱ）设每天获得的利润为y元，根据“每天获得的利润＝每件的利润×每天的销售量”列出函数解析式，配方成顶点式，再根据二次函数的性质求解即可．
【解答】解：（Ⅰ）①降价后每售一件该商品获得利润（40﹣x）元，
降价后平均每天售出（20+2x）件该商品，
故答案为：①40﹣x；②20+2x；

（Ⅱ）设每天获得的利润为y元，
根据题意，得：y＝（40﹣x）（20+2x）
＝﹣2x2+60x+800
＝﹣2（x﹣15）2+1250．
其中0≤x≤40，
∵﹣2＜0，
∴y有最大值，
∴当x＝15时，y有最大值为1250．
答：每件该商品应降价15元，获得最大利润为1250元．
【点评】本题主要考查二次函数的应用，解题的关键是理解题意找到题目蕴含的相等关系，并据此列出函数解析式，也要求对二次函数的性质熟练掌握．
25．如图乙，△ABC和△ADE是有公共顶点的等腰直角三角形，∠BAC＝∠DAE＝90°，点P为射线BD，CE的交点．

（1）如图甲，将△ADE绕点A旋转，当C、D、E在同一条直线上时，连接BD、BE，求证：BD＝CE；
（2）若AB＝6，AD＝3，把△ADE绕点A旋转：
①当∠CAE＝90°时，求PB的长；
②若M为线段BC中点，直接写出旋转过程中线段DM长的最大值．
【分析】（1）证明△BAD≌△CAE（SAS），可得结论；
（2）①分两种情形，分别画出图形，利用面积法求解，可得结论；
②连接AM，求出AM，可得结论．
【解答】（1）证明：如图甲中，

∵∠BAC＝∠DAE＝90°，
∴∠BAD＝∠CAE，
在△BAD和△CAE中，
，
∴△BAD≌△CAE（SAS），
∴BD＝CE．

（2）解：①当E在BA的延长线上时，

∵AB＝6，AD＝3，
∴EC＝BD3，
∵•CA•BE•EC•BP，
∴BP．
当点E在AB上时，

∵△BAD≌△CAE，
∴∠ABD＝∠ACE，
∵∠CEA＝∠BEP，
∴∠CPB＝∠CAE＝90°，
同法可求CP，
∴PB．
综上所述，满足条件的BP的值为或；

②如图3中，连接AM．

∵∠BAC＝90°，BCM，
∴AMBC＝3，
∵AD＝3，
∴DM≤AD+AM＝3+3，
∴DM的最大值为3+3．
【点评】本题属于几何变换综合题，考查了等腰直角三角形的判定和性质，全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，学会用分类讨论的思想思考问题，属于中考常考题型．
26．如图，已知抛物线y＝x2+bx+c的图象与x轴的一个交点为B（5，0），另一个交点A，且与y轴交于点C（0，5）．
（1）求直线BC与抛物线的解析式．
（2）若点M是抛物线在x轴下方图象上的一动点，过点M作MN∥y轴交BC于点N，求MN的最大值．
（3）在（2）的条件下，MN取得最大值时，若点P是抛物线在x轴下方图象上任意一点，以BC为边作平行四边形CBPQ，设平行四边形CBPQ的面积为S1，△ABN的面积为S2，且S1＝6S2，求点P的坐标．

【分析】（1）设直线BC的解析式为y＝mx+n，将B（5，0），C（0，5）两点的坐标代入，运用待定系数法即可求出直线BC的解析式；同理，将B（5，0），C（0，5）两点的坐标代入y＝x2+bx+c，运用待定系数法即可求出抛物线的解析式；
（2）MN的长是直线BC的函数值与抛物线的函数值的差，据此可得出一个关于MN的长和M点横坐标的函数关系式，根据函数的性质即可求出MN的最大值；
（3）先求出△ABN的面积S2＝5，则S1＝6S2＝30．再设平行四边形CBPQ的边BC上的高为BD，根据平行四边形的面积公式得出BD＝3，过点D作直线BC的平行线，交抛物线于点P，交x轴于点E，在直线DE上截取PQ＝BC，则四边形CBPQ为平行四边形．证明△EBD为等腰直角三角形，则BEBD＝6，求出E的坐标为（﹣1，0），运用待定系数法求出直线PQ的解析式为y＝﹣x﹣1，然后解方程组，即可求出点P的坐标．
【解答】解：（1）设直线BC的解析式为y＝mx+n，
将B（5，0），C（0，5）两点的坐标代入，得，
解得，
故直线BC的解析式为y＝﹣x+5；
将B（5，0），C（0，5）两点的坐标代入y＝x2+bx+c得，
解得．
故抛物线的解析式为y＝x2﹣6x+5；

（2）设M（x，x2﹣6x+5）（1＜x＜5），则N（x，﹣x+5），
∵MN＝（﹣x+5）﹣（x2﹣6x+5）＝﹣x2+5x＝﹣（x）2，
∴当x时，MN有最大值；

（3）∵MN取得最大值时，x＝2.5，
∴﹣x+5＝﹣2.5+5＝2.5，即N（2.5，2.5）．
解方程x2﹣6x+5＝0，得x＝1或5，
∴A（1，0），B（5，0），
∴AB＝5﹣1＝4，
∴△ABN的面积S24×2.5＝5，
∴平行四边形CBPQ的面积S1＝6S2＝30．
设平行四边形CBPQ的边BC上的高为BD，则BC⊥BD．
∵BC＝5，
∴BC•BD＝30，
∴BD＝3．
过点D作直线BC的平行线，交抛物线于点P，交x轴于点E，在直线DE上截取PQ＝BC，则四边形CBPQ为平行四边形．
∵BC⊥BD，∠OBC＝45°，
∴∠EBD＝45°，
∴△EBD为等腰直角三角形，BEBD＝6，
∵B（5，0），
∴E（﹣1，0），
设直线PQ的解析式为y＝﹣x+t，
将E（﹣1，0）代入，得1+t＝0，解得t＝﹣1
∴直线PQ的解析式为y＝﹣x﹣1．
解方程组，得，，
∴点P的坐标为P1（2，﹣3）（与点D重合）或P2（3，﹣4）．

【点评】本题考查了二次函数的综合题，其中涉及到运用待定系数法求一次函数、二次函数的解析式，二次函数的性质，三角形的面积，平行四边形的判定和性质等知识点，综合性较强，考查学生运用方程组、数形结合的思想方法．（2）中弄清线段MN长度的函数意义是关键，（3）中确定P与Q的位置是关键．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2023/1/19 14:12:34；用户：单静怡；邮箱：zhaoxia39@xyh.com；学号：39428212