2023年高考数学二轮复习重点基础练习：专题十 考点29 线性规划（C卷）

这是一份2023年高考数学二轮复习重点基础练习：专题十 考点29 线性规划（C卷），共10页。试卷主要包含了若实数满足约束条件则的最大值是，已知实数满足则的最小值为，若满足则的最大值为，若实数x，y满足约束条件且，则等内容，欢迎下载使用。
专题十 考点29 线性规划（C卷）1.已知x，y满足不等式组则的最大值为(   )A.12 B.10 C. D.22.若实数满足约束条件则的最大值是(   )A. B. C.1 D.23.已知实数满足则的最小值为(   )A.-7 B.-6 C.1 D.64.若满足则的最大值为(   )A.2 B.5 C.6 D.75.点满足不等式组设此不等式组围成的平面区域是M.若曲线和区域M有公共点，则实数a的取值范围为(   )A. B. C. D.6.已知x，y满足约束条件，则的最大值是(   )A. B. C.1 D.27.若实数x，y满足约束条件则的取值范围是(   )A. B. C. D.8.若实数x，y满足约束条件且，则(   )A.a有最小值  B.a有最大值-2C.a有最小值2  D.a有最大值9.已知实数满足不等式组，则的最小值为(   )A. B. C.11 D.1310.若实数满足约束条件，则的取值范围是(   )A. B. C. D.11.若实数x，y满足约束条件则的最大值为_____.12.若实数满足目标函数的最大值为a，最小值为b，则____________.13.若满足约束条件设，则z的取值范围为_____________.14.若x，y满足约束条件，则的最大值是___________.15.已知实数x，y满足则的最大值为________.
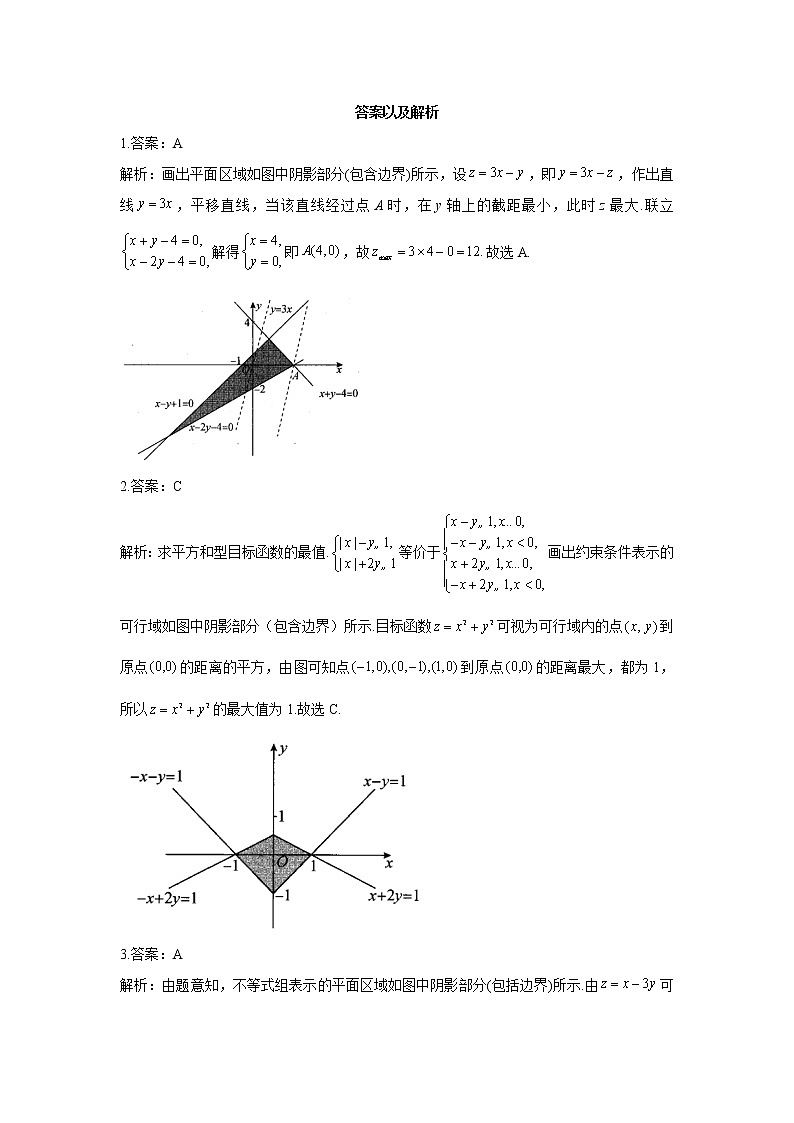
答案以及解析1.答案：A解析：画出平面区域如图中阴影部分(包含边界)所示，设，即，作出直线，平移直线，当该直线经过点A时，在y轴上的截距最小，此时z最大.联立解得即，故故选A.
 2.答案：C解析：求平方和型目标函数的最值.等价于画出约束条件表示的可行域如图中阴影部分（包含边界）所示.目标函数可视为可行域内的点到原点的距离的平方，由图可知点到原点的距离最大，都为1，所以的最大值为1.故选C.
 3.答案：A解析：由题意知，不等式组表示的平面区域如图中阴影部分(包括边界)所示.由可知.作出直线平移直线，当直线在y轴的截距最大时，目标函数z取得最小值.由图可知，当直线经过点A时，z取得最小值.联立解得即，因此故选A.
 4.答案：B解析：由约束条件作出可行域如图中阴影部分（包含边界）所示.设，则，作出直线，并平移该直线，当直线经过点A时，在y轴上的截距最大，此时z最大.由解得即，则.故选B.
 5.答案：A解析：画出不等式组所表示的平面区域如图中阴影部分所示（包括边界），因为当曲线过点时，，且时，，所以若曲线和区域M有公共点，则需满足.
 6.答案：C解析：作出不等式组表示的平面区域如图中阴影部分所示，作出直线并平移，结合图形可知，当平移后的直线过点A时，取得最大值.由，得，即，故.7.答案：D解析：画出约束条件所表示的区域，如图中阴影部分所示，表示可行域内的点与点连线的斜率，由图可知，点与点P连线的斜率最大，且，点与点P连线的斜率最小，且，因此，所求的取值范围是，故选D.8.答案：A解析：作出可行域如图中阴影部分所示.易知直线过定点，当时，由，得.数形结合知最小，即a的最小值为；最大，且易知，即a的最大值为.故选A.9.答案：B解析：法一：作出可行域如图中阴影部分所示.由得，由图形可知当直线过点B时，直线在y轴上的截距最小，此时z最小.由，得，得.法二：作出不等式组表示的平面区域如解法一图中阴影部分所示，易得.当直线过点时，；当直线过点时，；当直线过点时，.故的最小值是.10.答案：D解析：作出约束条件，所表示的平面区域，为如图所示的区域（包含边界）.表示阴影区域内的点与点连线的斜率.结合图形可知，点与点P的连线的斜率最大，且，点与点P的连线的斜率最小，且，因此，的取值范围是，故选D.11.答案：8解析：作出不等式组表示的平面区域如图中阴影部分（含边界）所示，结合目标函数的几何意义可知目标函数z在点处取得最大值，此时.
 12.答案：8解析：作出满足的约束条件对应的可行域，如图阴影部分所示，

由可得，易知直线经过点A，点B时，z分别取得最小值，最大值，联立解得，联立解得，
则，所以.13.答案：解析：作出满足的约束条件对应的可行域，如图阴影部分所示，

表示阴影部分中一点与点连线的斜率，
易得，
所以，所以z的取值范围为.14.答案：7解析：作出约束条件表示的可行域如图阴影部分所示，目标函数可化为直线，
当直线过点A时其在y轴上的截距最大，此时目标函数取得最大值，
联立，解得，
所以的最大值为.
 15.答案：8解析：作出不等式组表示的平面区域如图中阴影部分（含边界）所示，为以点三点为顶点的三角形区城，易知当直线等经过点时，目标函数z取得最大值，最大值为8.